Локальная и интегральная теоремы Муавра-Лапласа
Локальная теорема применяется для приближенного вычисления вероятности 
в пнезависимых испытаниях Бернулли при больших значениях пи возможно т.
Теорема. Вероятность того, что в п независимых испытаниях успех наступит ровно траз равна
,
где р– вероятность успеха в каждом испытании;
вероятность противоположного события;
.
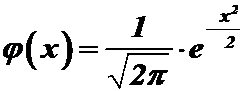Таблица значений функции 
приведена в приложении 1. Функция 
четная.
Пример 1. В сентябре в среднем бывает 10 дождливых дней. Определить, какова вероятность того, что в этом году в сентябре дождливых окажется 8 дней.
Решение. В сентябре 30 дней. Вероятность того, что произвольно выбранный сентябрьский день будет дождливым:
.
Вероятность того, что дождливых дней в этом сентябре окажется 8, равно:
.
Интегральная теорема Лапласа применяется для приближенного вычисления вероятности из писпытаний 
:
в п независимых испытаниях Бернулли при больших 
.
Теорема. Вероятность того, что в пнезависимых испытаниях число успехов т находится между 
и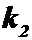 
, равна
,
где 
функция Лапласа, таблица значений которой приведена в приложении 2. 
нечетная, т.е. 
.
Пример 2.5% студентов вуза учатся только на «отлично». Какова вероятность того, что среди 700 студентов технологического факультета не меньше 32 и не больше 37 человек сдадут зимнюю сессию на «отлично»?
Решение. Вероятность быть отличником 
. Пусть т – число студентов, сдавших сессию на «отлично», тогда:
|
|
|
.
Дискретные случайные величины.
Закон распределения вероятностей. Функция распределения
Определение. Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения.
Пример 1.
1) Бросание игральной кости. Число очков – это случайная величина, ее возможные значения: 1, 2, 3, 4, 5, 6;
2) Число солнечных дней в марте – случайная величина: 1, 2, …, 31;
3) Вес зерен пшеницы, выращенных на одном участке – случайная величина, т.к. мы можем приблизительно задать интервал 
, в котором располагается вес зерен.
Из приведенных примеров видно, что случайные величины могут быть непрерывными(сплошь заполняющие некоторый интервал) и дискретными(принимающие отдельные значения).
Определение. Дискретнойслучайной величиной называется величина, значения которой есть конечное или счетное множество фиксированных величин.
Случайные величины будет обозначать большими буквами 
, а их возможные значения прописными: 
.
Для описания поведения дискретной случайной величины Х задают все значения , которые она может принять и вероятности появления этих значений 
.
Определение. Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причем 
:
|
|
|
| Х | 
| 
| 
| 
|
| Р | 
| 
|
| 
|
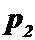
Говорят, что дискретная случайная величина Хподчинена данному закону распределения, если она задана одной из форм задания этого закона:
1) табулированное представление данной случайной величины в виде ряда распределения:
| Х |
|
|
|
|
| Р |
|
|
|
|
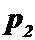
2) в виде формул конкретных распределений:
а) 
биномиальное;
б) 
гипергеометрическое;
в) 
закон Пуассона.
3) графически, откладывая на горизонтальной оси значения Х, а на вертикальной – соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.
Для дискретной случайной величины можно ввести понятие функции распределения 
.
Определение. Функцией распределения случайной величины Х называется функция, которая равна вероятности случайного события, состоящего в том, что дискретная случайная величина Х примет одно из возможных значений, меньших некоторого значения х, т.е.
.
Функцию распределения можно представить графически в виде ступенчатой функции (см. рис. 2).
|
|
|
Рис. 2
Если значения дискретной случайной величины расположены в порядке возрастания, то можно задать в виде:
Дата добавления: 2018-08-06; просмотров: 326; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!