Задачі для самостійного розв’язання

⇐ ПредыдущаяСтр 10 из 28Следующая ⇒

Задача 5.1. За даним рівнянням руху точки на довільно обраній траєкторії побудувати через рівні проміжки часу шість положень точки, визначити відстань s по траєкторії від початку відліку до кінцевого положення точки і пройдений нею шлях за вказаний проміжок часу (s і – в сантиметрах, t – в секундах):

1) , .

Відповідь: s=10см, =13см.

2) , .

Відповідь: s= –0,25см, =3,25см.

3) , .

Відповідь: s=0см, =20см.

Задача 5.2. За даними рівняннями руху точки знайти рівняння її траєкторії в координатній формі й вказати на рисунку напрямок руху:

1) , .

Відповідь: напівпряма 2х+3у–2=0 з початком у точці х = – 5, у = 4.

2) , .

Відповідь: права вітка параболи у=2х² з початковою точкою х=0, у=0.

3) , .

Відповідь: еліпс з початковою точкою х = 0, у = 3.

4) , .

Відповідь: еліпс з початковою точкою х = –1, у = –1.

Задача 5.3. За заданими рівняннями руху точки знайти рівняння її траєкторії, а також вказати закон руху точки по цій траєкторії, відраховуючи відстань від початкового положення точки:

1) , .

Відповідь: напівпряма 4х–3у=0, s=5t².

2) , .

Відповідь: коло х²+у²=9, s=3t.

3) , .

Відповідь: відрізок прямої х+у–а=0, 0≤х≤а, .

4) , .

Відповідь: коло х²+у²=25, s=25t².

Задача 5.4. Дані рівняння руху снаряда:

, ,

де v₀ – початкова швидкість снаряда; 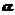– кут між і горизонтальною віссю х; – прискорення вільного падіння.

Знайти траєкторію руху снаряда, висоту Н, дальність L і час Т його польоту.

Відповідь: траєкторія – парабола , , , .

Задача 5.5. В умовах попередньої задачі визначити, при якому куті кидання 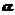дальність польоту L буде максимальною. Знайти відповідні висоту і час польоту.

Відповідь: α=45⁰, , , .

Задача 5.6. Кривошип ОА обертається зі сталою кутовою швидкістю . Довжина ОА=АВ=80см. Знайти рівняння руху і траєкторію середньої точки М шатуна, а також рівняння руху повзуна В, якщо в початковий момент повзун знаходився в крайньому правому положенні, осі координат вказані на рисунку.

Відповідь: 1) х_М=120cos10t, y_M=40sin10t ;

2) траєкторією точки М є еліпс ;

3)рівняння руху повзуна В: х=160cos10t.

Практичне заняття №6

Тема: Швидкість та прискорення матеріальної точки

Програмні питання

Середня швидкість матеріальної точки за проміжок часу ∆t. Вектор швидкості матеріальної точки в даний момент часу. Середнє прискорення точки за проміжок часу ∆t. Вектор прискорення матеріальної точки в даний момент часу. Визначення швидкості та прискорення точки при координатному і натуральному способах задання її руху.

Деякі поодинокі випадки руху точки: прямолінійний, рівномірний та рівнозмінний криволінійний, рівномірний та рівнозмінний прямолінійний.

Література

1. Курок В.П. Технічна механіка. Курс лекцій: навч. посіб. для студ. вищих навч. закл. – К.: Пед. преса, 2007. – 272с., л.10, л.11.

2. Курок В.П. Технічна механіка. Розділ: Кінематика: навч. посібник. – К., 2004. – 90 с., §§3 – 6.

3. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 1986. – 416с., §§. 38 – 45.

4. Никитин Е.М. Краткий курс теоретической механики. – М.: Наука, 1983. – 400с., §§. 44 – 49.

5. Цасюк В.В. Теоретична механіка: Навчальний посібник. – К.: Центр навчальної літератури, 2004. – 402с., §§8.4 – 8.7.

6. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука, 1986.–448с.

Короткі теоретичні відомості

Однією з важливих кінематичних характеристик руху точки є її швидкість, яка є мірою руху точки і характеризує бистроту зміни її положення з плином часу. Швидкість – величина векторна.

Відношення вектора переміщення точки до проміжку часу Δt назвемо середньою за модулем і напрямком швидкістю точки за цей проміжок часу Δt,тобто:

Середня швидкість напрямлена вздовж переміщення точки в бік її руху.

Швидкістю точки в даний момент часу називається векторна величина ,до якої прямує швидкість з наближенням проміжку часу до нуля. А оскільки граничне значення відношення приDt®0 є не що інше, як перша похідна від вектора по аргументуt, то маємо:

Отже, вектор швидкості в даний момент часу дорівнює першій похідній від радіуса-вектора точки за часом.

Величина, яка характеризує бистроту зміни швидкості точки з плином часу (як за модулем, так і за напрямком), називається прискоренням точки. Прискорення – величина векторна.

Відношення приросту вектора швидкості до проміжку часу ∆t визначає вектор середнього прискорення точки за цей проміжок часу:

Напрямок вектора , як видно, збігається з напрямком .

Прискоренням точки в даний момент часу називається векторна величина , до якої прямує середнє прискорення з наближенням проміжку часу Δt до нуля:

або .

Отже, вектор прискорення точки в даний момент часу дорівнює першій похідній від вектора швидкості або другій похідній від радіуса-вектора точки за часом.

У загальному випадку вектор лежить у стичній площині й напрямлений у бік угнутості кривої.

Визначення швидкості й прискорення точки при координатному способі задання її руху

Проекції вектора швидкості точки на осі координат дорівнюють першим похідним від відповідних координат точки за часом:

Знайдемо модуль і напрямок вектора швидкості за формулами:

;

Проекції вектора прискорення точки на координатні осі дорівнюють першимпохідним від проекцій вектора швидкості або другим похідним від відповідних координат точки за часом:

Модуль і напрямок прискорення визначаються за формулами:

Визначення швидкості й прискорення точки при натуральному способі задання її руху

Числова величина швидкості в даний момент часу дорівнює першій похідній від відстані (криволінійної координати) s точки за часом:

Вектор швидкості напрямлений по дотичній до траєкторії точки, причому, якщо v>0 , то в додатному напрямку відліку відстані, а якщо v<0, то у від'ємному (рис. 26).

Прискорення при натуральному способі задання руху точки визначається через його проекції на осі натурального тригранника Мτnb: дотичну вісь Мτ, напрямлену по дотичній до траєкторії руху точки в бік додатного відліку відстані, та головну нормаль Мп, яка лежить у стичній площині й напрямлена в бік угнутості кривої.

Проекція вектора прискорення точки на дотичну вісь дорівнює першій похідній від числової величини швидкості або другій похідній від відстані (криволінійної координати) sза часом, а проекція вектора прискорення на головну нормаль дорівнює квадрату швидкості, поділеному на радіус кривизни траєкторії в даній точці кривої:

Рис.26

Повне прискорення визначимо як геометричну суму складових (рис.26):

Перший доданок у рівнянні називається дотичним прискоренням, а другий – нормальним. Вектор напрямлений завжди в бік угнутості кривої (величина завжди додатна), а може бути напрямлений або в додатному, або у від'ємному напрямку осі Мτ, що залежить від знака проекції .Оскільки вектор нормального прискорення напрямлений до центра кривизни траєкторії, то його ще називають доцентровим.

Розглянемо деякі поодинокі випадки руху матеріальної точки.

1.Прямолінійний рух. Якщо траєкторією точки є пряма лінія, то ρ=∞,тоді , і повне прискорення точки дорівнює одному тільки дотичному прискоренню:

2. Рівномірний криволінійний рух. Рівномірним називається такий криволінійний рух точки, в якому числове значення швидкості весь час залишається сталим (v=const). Тоді,і повне прискорення дорівнює одному тільки нормальному прискоренню:

3.Рівномірний прямолінійний рух. У цьому випадку a_n=a_τ=0, а отже, a=0. Це єдиний рух, в якому прискорення точки весь час дорівнює нулю.

4.Рівнозмінний криволінійний рух. Рівнозмінним називається такий криволінійний рух точки, в якому дотичне прискорення залишається весь час сталим: a_τ= const.

Закон рівнозмінного криволінійного руху точки:

v=v₀+a_τt;

Приклади розв’язання задач

Задача 1. Точка рухається згідно рівнянь (t – в секундах, x, y – в метрах). Визначити величину і напрямок швидкості й прискорення точки в момент часу t=1c.

Розв’язання

Визначимо проекції швидкості точки на осі координат xта y:

v_x= =3t², v_y= =4t+1.

Модуль швидкості:

v= = = (м/с).

У момент часу t=1c: v= = =5,9(м/с).

Знаходимо напрямні косинуси :

соs( ,ˆx)= = ; соs( ,ˆy)= = .

Визначимо проекції вектора прискорення точки на координатні осі xта y:

а_x= =6t, а_y= =4.

Модуль прискорення: a= (м/с²).

У момент часу t=1c: a = (м/с²).

Напрямні косинуси:

соs( ,ˆx)= = =0,83; соs( ,ˆy)= = =0,55.

Задача 2. Автомобіль, маючи початкову швидкість v₀=36км/год, пройшов s=500м у перші t=20c. Вважаючи рух автомобіля рівнозмінним, визначити швидкість і прискорення автомобіля в кінці 20с, якщо рух автомобіля проходить по закругленню радіусом R=800м.