Вопрос 4. Числа натуральные, рациональные, иррациональные, алгебраические, трансцендентные. Принцип математической индукции.

Вопрос 1. Операции над множествами. Логические символы.

Множество - совокупность некоторых различимых объектов.

N - натуральные числа, Z- целые числа, Q - рациональные числа, R - вещественные числа, [a,b]– отрезок, (a, b) – интервал, (a,b],[a,b) – полуинтервалы.

Основные операции над множествами:

Элемент принадлежит множеству x E, элемент непринадлежитмножествуx E.

Подмножество A Ì E.

Æ- пустое множество 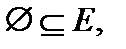EÍE.

Обозначение множества перечислением - {a, b, c}.

Обозначение множества указанием характеризующего свойства – {x: x удовлетворяет свойству P}.

Пример: N={xÎZ: x > 0}; [a,b]={x: a£x£b}

Дополнение множества A (или разность двух множеств)

E\A={xÎE: xÏA}

Пересечение двух множеств AÇB ={x: xÎA и xÎB}

Если два множества не пересекаются, то это можно записать в виде AÇB=Æ.

Объединение двух множеств AÈB ={x: xÎA или xÎB}

Произведение множеств A´B ={(x,y): xÎA и yÎB}.

Логические символы:

Вместо слов «существует, найдется, имеется» употребляем символ $ (Exist – “существует”).

Вместо слов «любой, каждый, произвольный» употребляем символ " (Any – “любой”).

Þ - следует

- равносильность

:= - равенство по определению

Вопрос 2. Понятие отображения, функции. Определение отображения сюръективного, инъективного, биективного, обратного. Композиция функций.

X, Y. Определяют соответствие при котором xÎX соответствует единственный элемент yÎY называется заданной функцией (определенной на множестве значений).

Оно называется также отображение Х в множестве Y, такая функция обозначается:

Y=f(x), xÎX

f: X→Y; x→y, xÎX, yÎY

Отображение f: X→Y называется сюръективным, если каждый элемент множества Y является образом хотя бы одного элемента множества X, то есть "yÎY $ xÎX: y=f(x).

Отображение f: X→Y называется инъективным, если для "x₁,x₂ÎXимеем

(f(x₁)= f(x₂)) (x₁=x₂) т.е. различные элементы имеют различные образы.

Биекция — это отображение, которое является одновременно и сюръективным и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием).

Если f: X→Y и g: Y→Z две функции то F: X→Z называется композицией функций (F(x)=g(f(x))) f и g или сложной функцией и обозначается g○f. (g○f)(x):=g(f(x)), "xÎX.

Вопрос 3. Аксиоматическое определение действительных чисел (свойства сложения и умножения, упорядоченность, плотность, непрерывность).

Множество называется множеством действительных чисел, а его элементы — действительными числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:

1. Операции сложение (для любой пары действительных чисел):

1.1) Коммутативность сложения: a + b = b + a

1.2) Ассоциативность сложения: a + ( b + c ) = ( a + b ) + c

1.3) Существование нуля: $0(существует элемент называемый нулем)"aÎR : a + 0 = a

1.4) Существование противоположного элемента: "a $ противоположный - a : a + (-a) = 0

2. Операции умножения (для любой пары действительных чисел):

2.1) Коммутативность умножения: a·b = b·a

2.2) Ассоциативность умножения: a·(b·c) = (a·b)·c

2.3) Существование единицы: существует элемент обозначаемый 1, "aÎR : 1·a = a

2.4) Существование обратного элемента: "aÎR a¹0 $a^-1(обратный): a·a ^-1 = 1

3) Операции сложения и умножения:

3.1) (a + b)·c = a·c + b·c ( дистрибутивность )

4) Упорядоченность:

4.1) Транзитивность: a < b, b < c Þ a < c

4.2) Связь сложения и порядка: если a<b "cÎR: a+c<b+с

4.3) Связь умножения и порядка: если a>b, c>0: a·c>b·c

       4.4)      Антисимметричность: если a≤b, b≤a: a=b

       Из 4.2 и 4.3 вытекает важное свойство плотность действительных чисел.Для любых двух действительных чисел a, b при a<b существует число с,такое что a<c<b.

5) Непрерывность:

       5.1) Пусть X,Y-непустые множества действительных чисел такие, что xÎX, yÎY, x ≤ y тогда $aÎR такое что: x ≤ a ≤ y

Вопрос 4. Числа натуральные, рациональные, иррациональные, алгебраические, трансцендентные. Принцип математической индукции.

       Натуральные числа - это числа, которые используются для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов.

       Рациональные числа- число, представляемое несократимой обыкновенной дробью m/n, где числитель m — целое число, а знаменатель n — натуральное число.

       Иррациональные числа- это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби m/n, где m — целое число, n — натуральное число.

       Алгебраические числа - называются корни алгебраических уравнений с целочисленными коэффициентами.

       Трансцендентные числа -число, которое не может быть корнем многочлена с целыми коэффициентами (число π; основание натуральных логарифмов е; десятичный логарифм любого целого числа, кроме чисел вида 10ⁿ).

       Принцип математической индукции:Множество AÌ N , если выполняются свойства:

1. 1ÎА

2. nÎА (nÎN)   n+1ÎА, тогда A=N

Док-во: Последовательно убеждаемся, что 2ÎА:=1+1, 3ÎА:=2+1, …, следовательно NÌ A, отсюда и из AÌNÞ A=N.

Вопрос 5. Расширенная числовая прямая . Промежутки, e-окрестности и e-полуокрестности точек из .

           Расширенная числовая прямая (читается «эр с чертой») — множество вещественных чисел , дополненное двумя элементами: (положительная бесконечность +¥) и (отрицательная бесконечность -¥), то есть =RÈ{-¥}È{+¥}.

           Промежуток - множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое число, лежащее между ними.

       e-окрестности - называется множество точек, удаленных от x₀ не более чем на ε, т.е.                 U(x₀,ε) :=(x₀-ε; x₀+ε).

       e-полуокрестности –называется множество точек, удаленных от x₀ либо слева, либо справа не более чем на ε, т.е. (x₀-ε, x₀] либо [x₀, x₀+ε).

Дата добавления: 2018-08-06; просмотров: 270; Мы поможем в написании вашей работы!
Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!