Часть 4. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Вентцель Г. С. Гл. 13, § 1 - 3, 5, 6 - 8. Гмурман В. Е. Гл. 9, гл. 12, § 8.

Роднищев Н.Е. Гл. 5.

При проведении испытаний малого объема такие характеристики случайных явлений, как относительная частота, средняя арифметическая результатов наблюдения и другие характеристики будут заметно меняться от одной серии испытаний к другой, т.е. не будут стабильными, устойчивыми. Однако если в этих сериях число испытаний очень велико, то указанные характеристики становятся стабильными, почти не изменяющимися. Это свойство нестабильности или стабильности характеристик случайных явлений в зависимости от числа испытаний в теории вероятности называется законом больших чисел.

Простейшей формой закона больших чисел является теорема Бернулли, которая утверждает, что при большом числе испытаний с вероятностью, близкой к единице относительная частота появления случайного события будет мало отличаться от вероятности этого события. Утверждение этой теоремы обосновывает общий, так называемый статистический метод определения вероятности случайного события как относительной частоты события при достаточно большом числе испытаний.

Более общая форма закона больших чисел выражается теоремой Чебышева. Она утверждает, что при достаточно большом числе независимых испытаний с вероятностью близкой к единице среднее арифметическое из наблюдавшихся значений случайной величины будет мало отличаться от математического ожидания этой величины. Утверждение этой теоремы обосновывает статистический метод определения математического ожидания, как среднего арифметического наблюдавшихся значений случайной величины при достаточно большом числе независимых испытаний.

Теоремы Бернулли и Чебышева, которые математически формулируются в терминах теории пределов, относят к так называемым предельным теоремам теории вероятностей. При доказательстве этих теорем используется неравенство Чебышева. Следует иметь в виду, что доказательство теоремы Бернулли целесообразно проводить после доказательства теоремы Чебышева.

В заключение этой части следует ознакомиться еще с одним типом предельных теорем теории вероятностей - центральной предельной теоремой (теоремой Ляпунова). Чтобы лучше уяснить смысл центральной предельной теоремы, следует обратить внимание, что в теоремах Бернулли и Чебышева законы распределения величин не рассматривались. В центральной предельной теореме устанавливается вид предельного закона распределения и указываются условия, при выполнении которых этот закон будет нормальным. Теорема Ляпунова объясняет, почему в реальных задачах производства, экономики и в других областях случайные величины имеют распределение, близкое к нормальному.

Вопросы для самопроверки: Роднищев Н.Е. стр. 81.

Вопросы для самопроверки

1. В чем состоит смысл закона больших чисел.

2. Как записывается неравенство Чебышева и какое теоретическое и практическое значение оно имеет.

3. Сформулировать теорему Чебышева.

4. Какое значение имеет теорема Чебышева для практики.

5. Сформулировать теорему Бернулли.

6. Какое практическое значение для практики имеет теорема Бернулли.

7. Сформулировать теорему Ляпунова.

8. В чем состоит смысл теоремы Ляпунова.

Примеры решения задач к части

4. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Задача 1. Используя неравенство Чебышева, оценить вероятность того, что непрерывная случайная величина отклонится по абсолютной величине от своего математического ожидания больше, чем на три средних квадратичных отклонений. Сравнить полученный результат с результатом, вытекающим из правила “трех сигм”.

Решение. Для решения задачи используем неравенство Чебышева в форме

По условию задачи . Используя это, неравенство Чебышева представим в виде

В соответствии с правилом “трех сигм” для непрерывных нормально распределенных случайных величин

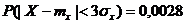Следовательно, неравенство Чебышева в данном случае дает завышенное значение вероятности выхода случайной величины X за трехсигмовый диапазон.

Задача 2. Сколько следует независимо проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных изделий от вероятности быть детали годной, равной 0,98, не превысит 0,02.

Решение. Обозначим искомое число независимых проверок величиной N. Далее, введем дискретную случайную величину X_i – число годных деталей при проверке i–й детали. Очевидно, закон распределения X_i будет следующий:

Х	0	1
Р	0,02	0,98

Относительная частота годных деталей при проверке N деталей равна

Х=(Х +Х +…+Х )/N.

Используя формулы для математического ожидания и дисперсии средней арифметической N независимых дискретных случайных величин, найдем

m =m =p, D =D /N=p(1-p)/N,

где р=0,98 – вероятность быть детали годной. В данной задаче вероятность быть детали годной равна математическому ожиданию Х.

Для решения задачи используем неравенство Чебышева, записанное для случайной величины Х, в форме

Р(|X-m |< )>1-D / .

По условию задачи =0,02. В результате получим

P(|X-m |<0,02)>1-(0,98*0,02)/0,02 *N.

Следовательно, 1-(0,98*0,02)/0,02 *N>0,96, откуда находим N>1225.

Задача 3. Вероятность того. Что каждое изделие будет высшего качества 0,3. Оценить вероятность того, что в 10000 испытаниях изделий на качество отклонение относительной частоты изделий высшего качества от вероятности быть изделию высшего качества по абсолютной величине не превзойдет 0,01.

Решение. Как и в предыдущей задаче рассмотрим относительную частоту Х=(Х +Х +…+Х ) /10000 изделий высшего качества. По формулам предыдущей задачи находим: m =0,03, D =0,3*0,7/10000=0,000021. Искомая вероятность находится с помощью неравенства Чебышева, записанного для случайной величины Х:Р(|X-m_x|< )>1-D / .По условию задачи =0,01. Следовательно, Р(|X-m_x|<0,01)>1-(0,3*0,7)/10000*0,01² =0,79.

Дата добавления: 2018-08-06; просмотров: 330; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Мы поможем в написании ваших работ!