Часть 3. СИСТЕМА СЛУЧАЙНЫХ ВЕЛИЧИН
Система случайных величин, её законы распределения и числовые характеристики
Вентцель Е.С.Гл. 8,§ 1-6,гл. 9,§ 1,3.
Гнурман В.Е.Гл. 14,§ 1-9, 11-19.
При изучении сложных явлений рассматриваются совместно две, три и большее число случайных величин, образующих комплекс, систему случайных величин. Здесь важно обратить внимание на то, что при исследовании характеристик системы случайных величин недостаточно изучить по отдельности характеристики каждой случайной величины, входящей в систему. Полными, исчерпывающими характеристиками системы случайных величин являются многомерные законы распределения. В случае системы дискретных величин - это многомерные таблицы распределения, а в случае непрерывных случайных величин – многомерная функция распределения или плотность вероятностей, которые являются обобщением соответствующих одномерных законов распределения случайной величины. Поскольку для систем с более, чем двумя случайными величинами отсутствуют простые геометрические представления законов распределения, то в основном при их изучении ограничиваются случаем систем с двумя случайными величинами.
При рассмотрении системы случайных величин важное значение имеют понятия зависимости и независимости случайных величин, входящих в систему. Эти понятия обобщают понятия зависимых и независимых событий. Изучающему данный раздел следует четко уяснить принципиальное отличие зависимости случайных величин, называемой вероятностной, от зависимости величин, рассматриваемой в математическом анализе, которая имеет характер жесткой зависимости между величинами. Вероятностная зависимость является общим видом зависимости величин.
|
|
|
При исследовании взаимосвязи двух случайных величин используются понятия условных законов распределения.
Для оценки степени зависимости случайных величин используется числовая характеристика – корелляционный момент, который при отсутствии связи между случайными величинами равен нулю, а с увеличением степени связи его значение возрастает.
Следует усвоить характерные для системы двух величин такие числовые характеристики, как условные математические ожидания и дисперсии, а так же связанные с этими характеристиками понятия линий регрессии.
Далее необходимо рассмотреть нормально распределенную систему двух непрерывных случайных величин, как частный, но имеющий большое практическое применение, случай систем случайных величин. Обратить внимание на выражение плотности вероятности системы, условия независимости двух случайных величин, на выражение условных плотностей вероятностей, условных математических ожиданий и дисперсий.
|
|
|
Между прочим, с использованием новой числовой характеристики – корреляционного момента – удается получить формулы для дисперсии суммы зависимых случайных величин, являющихся обобщением ранее рассмотренной формулы.
Вопросы для самопроверки.
1. Что называется системой случайных величин? Привести примеры системы случайных величин.
2. Дать определение функции распределения системы двух случайных величин и указать её свойства.
3. Дать определение плотности вероятностей системы двух случайных величин и перечислить свойства этой функции.
4. Как находится вероятность попадания системы случайных величин в заданную область?
5. Как выражается плотность вероятностей каждой случайной величины, входящей в систему через плотность вероятностей системы?
6. Дать определение условных плотностей вероятностей системы случайных величин и указать, как они связаны с плотностями распределения системы и каждой случайной величины, входящей в систему.
7. Какие две величины называются независимыми? зависимыми?
8. Запишите необходимое и достаточное условие независимости двух случайных величин.
|
|
|
9. Что называется корреляционным моментом? коэффициентом корреляции двух случайных величин? Указать область изменения значений коэффициентов корреляции.
10. Определить понятия условных математических ожиданий и дисперсии системы двух случайных величин.
11. Что такое линии регрессии системы двух случайных величин?
12. Чему равен коэффициент корреляции системы двух случайных величин?
13. Какие случайные величины называются некоррелированными?
14. Следует ли в общем случае из некоррелированности независимость случайных величин?
15. Какие числовые характеристики могут охарактеризовать систему нескольких случайных величин.
16. Что называют корреляционной и нормированной корреляционной матрицей системы нескольких случайных величин?
17. Записать выражение плотности вероятностей нормально распределенной системы двух непрерывных случайных величин..
18. Какое простое условие независимости двух случайных величин будет у нормально распределенной системы?
19. Привести формулу для вероятности попадания в заданный прямоугольник со сторонами, параллельным осям координат, для нормально распределенной системы.
20. Записать для условных плотностей вероятности, математических ожиданий и дисперсий, для нормально распределенной системы.
|
|
|
21. Рассмотреть линии регрессии нормально распределенной системы и проанализировать их характер расположения в зависимости от величины коэффициента корреляции.
22. Что такое эллипсы рассеивания для нормально распределенной системы?
23. Привести формулу для дисперсии суммы зависимых случайных величин.
Примеры решения задач к части
3.СИСТЕМА СЛУЧАЙНЫХ ВЕЛИЧИН
Задача 1. Задана двумерная функция распределения 
двумерной случайной величины 
Найти вероятность попадания случайной точки 
в прямоугольник, ограниченный прямыми 
, 
, 
, 
.
Решение. Определим вероятность попадания случайной точки в прямоугольник, ограниченный прямыми 
, 
, 
, 
по формуле
= ( 
− 
) − ( 
− 
) =
.
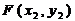Задача 2. Двумерная дискретная случайная величина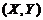 
описывается законом распределения вероятностей, заданного таблицей
  Y
| 
| 
|
|  0,10
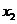
|  0,15
|
|  0,15
|  0,25
|
|  0,20
|  0,15
|
Определить закон распределения случайных величин 
и 
, условный закон распределения при условии, что 
и условный закон распределения при условии, что 
.
Решение. Для определения безусловных законов распределения случайных величин и воспользуемся формулой 
, тогда
,
,
.
Для величины аналогично получим
,
.
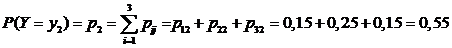Условный закон распределения при условии, что , определяется совокупностью условных вероятностей
,
,
.
Условный закон распределения при условии, что .определяется совокупностью условных вероятностей
,
,
Нетрудно видеть, что как безусловные, так и условные распределения вероятностей удовлетворяют условию нормировки, т.е. вероятности в сумме равны единице.
Задачи к части
3. СИСТЕМА СЛУЧАЙНЫХ ВЕЛИЧИН
1-5. Система двух дискретных случайных величин (X,Y) задана двумерной таблицей распределения:
| Y X | x1 | x2 | x3 |
| y1 | p11 | p21 | p31 |
| y2 | p12 | p22 | p32 |
Определить законы распределения дискретных случайных величин X,Y системы (X,Y). Найти математическое ожидание, дисперсию случайных величин X,Y и корреляционный момент системы (X,Y).
Исходные данные к задачам:
| №№ задачи | p11 | p21 | p31 | p12 | p22 | p32 |
| 1 | 0,1 | 0,2 | 0,3 | 0,15 | 0,2 | 0,05 |
| 2 | 0,25 | 0,1 | 0,2 | 0,25 | 0,15 | 0,05 |
| 3 | 0,1 | 0,3 | 0,05 | 0,2 | 0,05 | 0,3 |
| 4 | 0,3 | 0,005 | 0,3 | 0,15 | 0,1 | 0,1 |
| 5 | 0,1 | 0,2 | 0,25 | 0,05 | 0,25 | 0,15 |
6-10. Система двух дискретных случайных величин (Х,Y) задана двумерной таблицей распределения:
| X Y | x1 | x2 |
| y1 | p11 | p21 |
| y2 | p12 | p22 |
| y3 | p13 | p23 |
Определить законы распределения дискретных случайных величин Х,Y системы (Х,Y). Найти математическое ожидание, дисперсию случайных величин Х,Y и корреляционный момент системы (Х,Y).
Исходные данные к задачам:
| №№задачи | p11 | p21 | p12 | p22 | p13 | p23 |
| 6 | 0.1 | 0.15 | 0.2 | 0.25 | 0.25 | 0.05 |
| 7 | 0.25 | 0.25 | 0.1 | 0.15 | 0.2 | 0.05 |
| 8 | 0.1 | 0.2 | 0.3 | 0.05 | 0.05 | 0.3 |
| 9 | 0.3 | 0.05 | 0.3 | 0.15 | 0.1 | 0.1 |
| 10 | 0.2 | 0.1 | 0.05 | 0.25 | 0.25 | 0.15 |
11-15. Система двух дискретных случайных величин (Х,Y) задана двумерной таблицей распределения:
| X Y | x1 | x2 | x3 |
| y1 | p11 | p21 | p31 |
| y2 | p12 | p22 | p32 |
Определить условный закон распределения дискретной случайной величины Х при условии, что дискретная случайная величина Y приняла значения y1. Наити условные математическое ожидание M[Х/Y=y1] и дисперсию D[Х/Y=y1].
Исходные данные к задачам:
| №№задачи | p11 | p21 | p31 | p12 | p22 | p32 |
| 11 | 0.1 | 0.2 | 0.3 | 0.15 | 0.2 | 0.05 |
| 12 | 0.25 | 0.1 | 0.2 | 0.25 | 0.15 | 0.05 |
| 13 | 0.1 | 0.3 | 0.05 | 0.2 | 0.05 | 0.3 |
| 14 | 0.3 | 0.05 | 0.3 | 0.15 | 0.1 | 0.1 |
| 15 | 0.1 | 0.2 | 0.25 | 0.05 | 0.25 | 0.15 |
16-20. Система двух дискретных случайных величин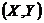 
задана двумерной таблицей распределения
| Y X | 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
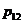
Определить условный закон распределения дискретной случайной величины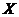 
при условии, что дискретная случайная величина 
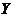приняла значение . Найти условные математическое ожидание 
и дисперсию 
.
Исходные данные к задачам:
| №№ задачи |
|
|
|
|
|
|
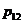
| 16 | 0,1 | 0,15 | 0,2 | 0,25 | 0,25 | 0,05 |
| 17 | 0,25 | 0,25 | 0,1 | 0,2 | 0,2 | 0,05 |
| 18 | 0,1 | 0,2 | 0,3 | 0,05 | 0,05 | 0,3 |
| 19 | 0,3 | 0,05 | 0,3 | 0,15 | 0,1 | 0,1 |
| 20 | 0,2 | 0,1 | 0,05 | 0,25 | 0,25 | 0,15 |
21-25. Вычислить вероятность попадания двумерной непрерывной случайной величины 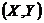с нормальным распределением в прямоугольник, ограниченный прямыми: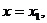 
, 
. Случайные величины 
независимы и имеют математические ожидания 
и средние квадратичные отклонения 
, 
:
| №№ задачи |
|
|
|
| 
|
|
|
|
| 21 | 1 | 2 | 2 | 3 | 1,5 | 2,5 | 0,5 | 1 |
| 22 | 2 | 3 | 1 | 2 | 0,9 | 1,5 | 0,6 | 2 |
| 23 | 1,5 | 2 | 2 | 3 | 1 | 2 | 0,8 | 1 |
| 24 | 2 | 4 | 0 | 3 | 1 | 2 | 0,5 | 0,8 |
| 25 | 3 | 5 | 3 | 5 | 0,5 | 4 | 0,8 | 0,5 |
26-30. Найти вероятность попадания двумерной непрерывной случайной величины 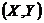в прямоугольник, ограниченный прямыми: ,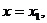 
Плотность вероятности 
системы 
внутри прямоугольника постоянная.
Исходные данные к задачам:
| № задачи | 
| 
| 
| 
|
| 26 | 0,5 | 2 | 1 | 5 |
| 27 | 0,2 | 2,5 | 1 | 4 |
| 28 | -1 | 1,5 | 0 | 3 |
| 29 | -0,5 | 2 | 1 | 5 |
| 30 | -1 | 1,5 | 0,5 | 2,5 |
31-35. Известны математические ожидания 
средние квадратичные отклонения 
и матрица К корреляционных моментов системы . Записи выражение плотности вероятности внутри системы .
Исходные данные к задачам:
| № задачи | 31 | 32 | 33 | 34 | 35 |
| 26 | 20 | 30 | 45 | 25 |
| 12 | 8 | 10 | 14 | 15 |
| К | 256 -90 -90 169 | 120 10 10 90 | 100 20 20 50 | 150 -20 -20 60 | 75 15 15 60 |
36-40. Система непрерывных случайных величин имеет постоянную плотность вероятностей в заданной области. Являются ли случайные величины независимыми? Если нет, то определить условные математические ожидания случайных величин .
Исходные данные к задачам:
| № задачи | Вид области |
| 36 | Внутренность треугольника с вершинами в точках (0,0), (1,0), (0,1) |
| 37 | Внутренность квадрата с вершинами в точках (0,0), (0,1), (1,0), (1,1) |
| 38 | Внутренность прямоугольника с вершинами в точках (0,0),(2,0),(0,1),(2,1) |
| 39 | Внутренность четверти единичного круга с центром в точке (0,0) |
| 40 | Внутренность половины единичного круга с центром в точке (0,0) |
41 – 45 . Для двух дискретных независимых случайных величин X, Y заданы законы распределения:
| X | x1 | x2 |
| P | p1 | P2 |
Найти двумерный закон распределения системы (X, Y), определить корреляционный момент системы (X, Y).
Исходные данные к задачам 41 – 45:
| № задачи | x1 | x2 | p1 | p2 | y1 | y2 | q1 | q2 |
| 41 | 1 | 2 | 0,1 | 0,9 | -1 | 1 | 0,3 | 0,7 |
| 42 | 3 | 4 | 0,2 | 0,8 | 0 | 2 | 0,2 | 0,8 |
| 43 | 5 | 6 | 0,3 | 0,7 | 1 | 2 | 0,1 | 0,9 |
| 44 | 0 | 2 | 0,4 | 0,6 | 3 | 4 | 0,4 | 0,6 |
| 45 | -1 | 1 | 0,25 | 0,75 | 2 | 3 | 0,5 | 0,5 |
Дата добавления: 2018-08-06; просмотров: 561; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!