Случайная величина, её закон распределения и числовые характеристики.

Вентцель Е.С. Гл. 2, § 4, гл..5, § 1- 8.

Гмурман В.Е. Гл. 6, §1-3, гл. 7, §1-4, гл.8

Роднищев Н.Е. Гл.3.

Понятие случайной величины – одно из основных в теории вероятностей. Во всех практических задачах, в которых применяются методы теории вероятностей, случайная величина – необходимый элемент исследования. Следует четко уяснить определение дискретных и непрерывных случайных величин и уметь приводить примеры этих типов случайных величин из производственной и экономической области. Далее необходимо усвоить понятие закона распределения вероятностей как полной, исчерпывающей характеристики случайной величины и его представление для дискретных случайных величин в форме таблицы распределения и многоугольника распределения, и для непрерывных случайных величин в виде функции распределения и плотности вероятностей.

Большое практическое значение в теории вероятностей имеют так называемые числовые характеристики случайных величин, которые, в отличие от закона распределения вероятностей, являются частными характеристиками, определяющими те или иные важные свойства случайной величины. Среди этих числовых характеристик наиболее существенные – математическое ожидание и дисперсия, которые являются частными случаями начальных и центральных моментов случайной величины. Изучая этот раздел, уяснить какие свойства случайной величины отражают её математическое ожидание и дисперсия.

Строго говоря, для определения математического ожидания и дисперсии изучаемых случайных величин необходимо знание закона распределения, но практически их можно находить опытным путем при проведении серии испытаний, что обосновывается в разделе предельных теорем, рассматриваемых в дальнейшем.

Следующими важным понятиями теории вероятностей являются понятия зависимости случайных величин. Необходимые и достаточные условия независимости случайных величин будут изучены в разделе «Системы случайных величин». Здесь же, опираясь на определение независимости случайных величин как независимость закона распределения вероятностей каждой из них от того, какие возможные значения принимают другие случайные величины, познакомиться с выводом формул для математического ожидания и дисперсии суммы независимых случайных величин.

Вопросы для самопроверки: Роднищев Н.Е. стр. 54.

Вопросы для самопроверки.

1. Сформировать определение дискретной и непрерывной случайной величины и привести примеры той и другой величины.

2. Какие формы представления законы распределения у дискретной величины?

3. Дать определение функции распределения непрерывной случайной величины и привести основные свойства.

4. Дать определение плотности вероятностей непрерывной случайной величины и указать основные свойства этой функции.

5. Как определяется вероятность попадания в заданный интервал случайной величины (дискретной и непрерывной)?

6. Указать связь, которая существует между функцией распределения и плотностью вероятностей.

7. Дать определение числовой характеристики – математического ожидания дискретной и непрерывной случайной величины.

8. Каков геометрический и вероятностный смысл математического ожидания?

9. Привести свойства математического ожидания.

10. Дать определение числовой характеристики – дисперсии дискретной и непрерывной случайной величины.

11. Для характеристики какого свойства случайной величины используется дисперсия (среднее квадратичное отклонение)?

12. Привести свойства дисперсии.

13. Что такое мода и медиана случайной величины?

14. Что называется начальным моментом и центральным моментом случайной величины?

15. Дать определение коэффициента асимметрии и эксцесса.

16. Охарактеризовать непрерывную случайную величину с равномерным распределением.

17. Дать определение зависимых и независимых случайных величин.

18. Проделать вывод формул для математического ожидания и дисперсии суммы независимых случайных величин.

Нормально распределенные непрерывные случайные величины.

Вентцель Е. С. Гл. 6.

Гмурман В. Е. Гл. 12.

Роднищев Н.Е. Гл.4.

Среди распределений непрерывных случайных величин центральное место занимает нормальный закон распределения (закон Гаусса). Этот закон распределения наиболее широко распространен в тех случаях, когда случайная величина является ре зультатом действия большого числа различных факторов, причем каждый фактор в отдельности на случайную величину влияет незначительно. Так случайными величинами, имеющими нормальное распределение, могут быть: отклонение действительных размеров деталей, выпускаемых станком-автоматом, ошибки измерения и т.п. Основная особенность нормального распределения, которая выделяет его из других распределений, заключается в том, что оно является предельным законом распределения, к которому приближаются другие распределения. В дальнейшем будет рассмотрена так называемая центральная предельная теорема теории вероятностей, в которой доказывается, что при достаточно большом числе независимых случайных величин, подчиненных некоторым законам распределения, их сумма будет иметь закон распределения сколь угодно близкий к нормальному.

При изучении этого раздела обратить внимание на ряд формул, имеющих большое практическое значение: на формулу для вероятности попадания нормально распределенной случайной величины на заданный интервал, на формулу для вероятности отклонения случайной величины от своего математического ожидания, по абсолютной величине не превышающего заданного значения.

Вопросы для самопроверки: Роднищев Н.Е. стр. 70.

Вопросы для самопроверки.

1. Какое распределение непрерывной случайной величины называется нормальным распределением?

2. Изобразить график плотности распределения вероятности нормального распределения и пояснить: как будет изменяться форма этого графика при изменении математического ожидания и среднего квадратичного отклонения?

3. Написать и пояснить формулу для определения вероятности попадания нормально распределенной случайной величины в заданный интервал. Что называется функцией Лапласа или интегралом вероятности, и каковы ее свойства?

4. Записать формулу для вероятности отклонения нормльно распределенной случайной величины от своего математического ожидания, по абсолютной величине не превышающего заданного значения.

5. В чем заключается правило «трех сигм»?

6. Чем объясняется широкое распространение на практике нормального распределения?

Примеры решения задач к части

2.СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Задача 1. Испытывается устройство, состоящее из двух независимо работающих приборов. Вероятности отказа приборов таковы: 0,2; 0,1. Найти математическое ожидание и дисперсию случайного числа отказавших приборов.

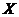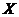Решение. Случайная величина Х – число отказавших приборов – в данной задаче может принимать случайно значения: 0, 1, 2 соответствующими веро ятностями. Определим эти вероятности. Значение , равное нулю, соответствует случаю, когда не откажет ни первый, ни второй прибор. Очевидно, . Значение , равное 1, отвечает случаю, когда первый прибор откажет, а второй нет, или второй прибор откажет, а первый нет. В этом случае 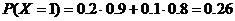. Наконец, значение 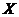, равное 2, соответствует случаю, когда откажут оба прибора совместно. Естественно, что 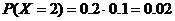. Легко убедится, что .

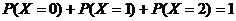Математическое ожидание случайной дискретной величины 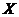определяется по формуле

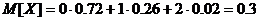Для вычисления дисперсии удобно воспользоваться формулой 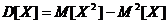. В результате вычислений получим

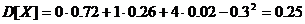Задача 2. Изделия независимо испытываются на надежность. вероятность для каждого изделия выйти из строя p. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Найти формулу для ряда распределения, определить математическое ожидание случайного числа испытаний.

Решение. Отметим, что в данной задаче испытания заканчиваются на i-м изделии (i=1,2,3,…), если первые i-1 изделия пройдут испытания, а i-е выйдет из строя.

Обозначим 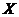- случайное число испытаний. Очевидно, что для ряда распределения можно записать следующую аналитическую формулу

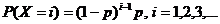
особенностью данной задачи является то, что i – число испытаний - представляет бесконечное счетное множество значений, причем вероятность 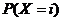при неограниченном росте i стремится к нулю. В силу свойства ряда распределения сумма всех вероятностей 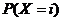должна равняться единице, т.е. 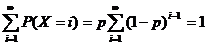. Убедимся в этом.

Ряд 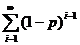представляет собой бесконечную убывающую геометрическую прогрессию со знаменателем 1-p и поэтому 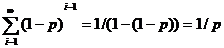. Следовательно, .

В соответствии с общей формулой, математическое ожидание дискретной случайной величины Х запишется следующим образом

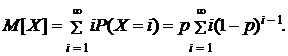
Вычислим ряд 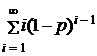. Для удобства введем величину q = 1-p. Тогда последний ряд запишется в виде 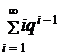, для вычисления которого воспользуемся следующим приемом.

Рассмотрим ряд, представляющий бесконечную убывающую геометрическую прогрессию: 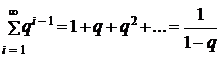. Продифференцировав последнее по q, будем иметь 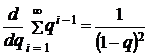. Левая часть этого равенства представляет ряд 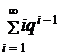. Возвращаясь к величине p, можем записать 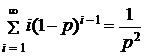. Таким образом, .

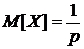Задача 3. Цилиндрические валики, изготовляемые автоматом, считаются стандартными, если отклонение диаметра валика от проектного размера не превышает 3 мкм. Случайные отклонения диаметра валика от проектного подчиняются нормальному распределению с параметрами m = 0, σ = 1,6 мкм. Сколько процентов стандартных валиков будет изготовлять автомат?

Решение. Обозначим через Х – случайные отклонения диаметра валика от проектного размера. Равенство математического ожидания нулю (m = 0) означает, что случайные отклонения будут группироваться около проектного размера (систематическая ошибка отклонения отсутствует).

Для определения вероятности события 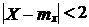мкм воспользуемся формулой теории вероятностей

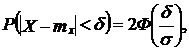
где 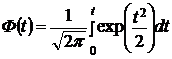- функция Лапласа (интеграл вероятности), δ – допустимое отклонение по абсолютной величине Х от своего математического ожидания (в данной задаче δ = 2 мкм, т = 0), σ – среднее квадратичное отклонение Х.

Искомая вероятность Р(|Х| < 2 мкм) = 2Ф(2/1,6) = 2Ф(1,25). По таблице функции Лапласа находим Р(|Х| < 2) = 0,789 = 78,9%.

Задача 4. Высотомер самолета имеет случайную и систематическую ошибки. Систематическая ошибка равна 20м. Случайная ошибка распределена нормально. Какое среднее квадратичное отклонение должна иметь случайная ошибка высотомера, чтобы с вероятностью 0.9 ошибка измерения высоты была меньше 100м.

Решение. Обозначим Н_ист - истинная высота полета самолета, Н – случайная величина – показание высотомера. По условию задачи задано, что вероятность события

Н_ист-100<Н<Н_ист+100

равна 0,9.

Для решения задачи воспользуемся формулой теории вероятностей для вероятности попадания случайной величины в заданный интервал

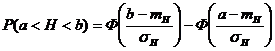где Ф(t), как и в предыдущей задаче, функция Лапласа. В данной задаче a=H_ист-100 м, b= H_ист+100 м. В результате можно записать

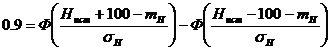Систематическая ошибка представляет собой неслучайную величину m_H- H_ист, которая по условию задачи равна 20м. С учетом этого приходи к следующему уравнению относительно s_Н:

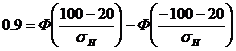Учитывая, что функция Лапласа – нечетная функция (Ф(-t)=-Ф(t)), окончательно запишем 0,9=Ф(80/s_Н)+Ф(120/s_Н). Последнее уравнение является трансцендентным, решение которого можно найти приближенно путем проб: s_Н»58 м.

Задачи к части

2.СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

1. Из партии в 25 изделий, среди которых 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить таблицу распределения дискретной случайной величины Х - числа бракованных изделий, и определить математическое ожидание этой случайной величины.

Ответ: 0,72.

2. Из партии в 25 изделий, среди которых 6 бракованных, выбраны случайным образом 3 изделия для проверки их качества. Построить таблицу распреде ления дискретной случайной величины Х – числа стандартных изделий, содержащихся в выборке из трех изделий, и определить математическое ожидание этой случайной величины.

3. При установившимся первым сортом и 1/3 – вторым. Построить таблицу распределения случайной величины Х – числа изделий первого сорта среди 5 изделий, отобранных случайным образом. Вычислить математическое ожидание и дисперсию рассматриваемой случайной величины.

Ответ: m_x = 3,33: D_x = 1,11.

4. Производятся независимые испытания трех приборов. Вероятность отказа каждого прибора соответственно равны p₁, p₂, p₃. Доказать,что математическое ожидание числа отказавших приборов равна p₁ + p₂ + p₃.

5. Автоматическая линия при нормальной настройке может выпускать бракованные агрегаты вероятностью p. Переналадка линии производится сразу после первого бракованного агрегата. Найти среднее число всех агрегатов, изготовленных между двумя переналадками линии.

Ответ: 1/p.

6.Партия из 100 изделий содержит 10 бракованных. Из этой партии извлекается случайным образом 5 изделий. Изобразить таблицу распределения дискретной случайной величины Х – числа бракованных изделий в выборке и определить ее математическое ожидание.

Ответ: 0.5.

7. Известно, что в партии из 100 изделий содержится 10 нестандартных. Из партии извлекается случайная выборка из 5 изделий. Построить таблицу распределения дискретной случайной величины Х – числа стандартных деталей в выборке и определить ее математическое ожидание.

Ответ: 4,5.

8. Определить математическое ожидание числа приборов, давших отказ за время испытаний на надежность, если испытанию подвергнется один прибор, а вероятность его отказа p.

Ответ: p.

9. В партии из 10 деталей имеется одна бракованная. Чтобы ее обнаружить, выбирают в случайном порядке одну деталь за другой и каждую проверяют. Пусть Х – число проверенных деталей, включая бракованную. Найти закон распределения, математическое ожидание и дисперсию дискретной случайной величины Х.

Ответ: 5,5; 8,25.

10. Независимые испытания аппаратуры повторяются до тех пор, пока она не дает отказ. Вероятность отказа аппаратуры от испытания к испытанию меняется и равна p. Найти математическое ожидание случайного числа безотказных испытаний аппаратуры.

Ответ: (1-р)/р.

11. Испытывается агрегат, состоящий из четырех независимо работающих элементов, вероятность отказа которых следующие: 0,3; 0,4; 0,5; 0,6. Вычислить математическое ожидание и дисперсию числа отказавших приборов.

Ответ 1,8; 0,94.

12. Производятся независимые испытания N изделий на надежность, причем вероятность выдержать испытания для каждого изделия одинакова и равна p. Записать выражение для ряда распределения случайного числа изделий, выдержавших испытания, и найти его математическое ожидание.

Указание: использовать формулу Бернулли.

13. Испытываются независимо N агрегатов на надежность. Вероятность не выдержать испытания у каждого изделия одинакова и равна p. Записать выражение для ряда распределения случайного числа агрегатов, которые прошли испытание на надежность, и найти его математическое ожидание.

Указание: использовать формулу Бернулли.

14. Измерительный прибор имеет систематическую ошибку 5 м и среднее квадратичное отклонение 50 м. Какова вероятность того, что нормально распределенная ошибка измерения не превзойдет по абсолютной величине 5м?

Ответ: Р=0,0793.

15. Какой ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины допуска подчиняются нормальному распределению с параметрами m = 0, 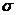= 5 мкм?

Ответ: не менее 30 мкм.

16. Коробки с шоколадом упаковываются автоматом. Их средняя масса равна 1,06 кг. Найти среднее квадратичное отклонение, если 5% коробок имеет массу меньше 1 кг. Предполагается, что масса коробок имеет нормальное распределение.

Ответ: 0,0306 кг.

17. Случайные ошибки измерения двумя измерительными приборами подчинены нормальному закону с m_1.2=0_и_ 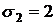мкм. Определить вероятность того, что из двух независимых измерений в каждом

из них ошибки измерения по абсолютной величине не превышают 1,5 мкм.

Ответ: 0,4644.

18. Дальность до объекта определяется дальномером, средняя квадратичная ошибка которого 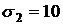, систематическая ошибка +5 м. Ошибка измерения имеет нормальное распределение. Найти вероятность того, что измеренное значение не отклонится от истинного более чем на 15 м.

Ответ: 0,1813.

19. Дальность до объекта определяется дальномером, средняя квадратичная ошибка которого 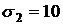, систематическая ошибка +5 м. Ошибка измерения имеет нормальное распределение. Найти вероятность того, что измеренное значение не превзойдёт истинное более чем на 15 м.

Ответ: 0,8414.

20. Дальность до объекта определяется дальномером, средняя квадратичная ошибка которого 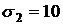, систематическая ошибка +5 м. Ошибка измерения имеет нормальное распределение. Найти вероятность того, что измеренное значение превысит истинное более чем на 20 м.

Ответ: 0,0668.

21. Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону со средним квадратичным отклонением 3 мм. Систематические ошибки отсутствуют. Определить среднее число изделий высшего качества, если изготовлено 4 изделия.

Ответ: 3 изделия.

22. Систематическая ошибка удержания высоты самолётом +20 м, а случайная нормально распределённая ошибка характеризуется средним квадратичным отклонением, равным 50 м. Для полёта самолёта отведён коридор высотой 100 м. Какова вероятность, что самолёт будет лететь выше, коридора, если самолёту задана высота, соответствующая середине коридора.

Ответ: 0,0548.

23. Систематическая ошибка удержания высоты самолетом +20 м, а случайная нормально распределенная ошибка характеризуется средним квадратичным отклонением, равным 50 м. Для полета самолета отведен коридор высотой 2 100 м. Какова вероятность, что самолет будет лететь ниже коридора, если самолету задана высота, соответствующая середине коридора.

Ответ: 0,0082.

24. Систематическая ошибка удержания высоты самолетом +20 м, а случайная нормально распределенная ошибка характеризуется средним квадратичным отклонением, равным 50 м. Для полета самолета отведен коридор высотой 2 100 м. Какова вероятность, что самолет будет лететь внутри коридора, если самолету задана высота, соответствующая середине коридора.

Ответ: 0,9452.

25. На производственном участке за одну смену изготавливается 100 изделий, содержащих 10% брака. Вся эта партия принимается, если годными оказываются выбранные случайным образом 4 изделия. В противном случае вся партия бракуется. Найти математическое ожидание числа забракованных партий изделий, изготовленных в течение трех смен.

Ответ: 0,00015.

26. На производственном участке за одну смену изготавливается 100 изделий, содержащих 10% брака. Вся эта партия принимается, если годными оказываются выбранные случайным образом 4 изделия. В противном случае вся партия бракуется. Найти математическое ожидание числа незабракованных партий изделий, изготовленных в течение трех смен.

Ответ: 0,99985.

27. Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует наладки, равны соответственно: 0,85; 0,9; 0,95. Построить ряд распределения и найти математическое ожидание числа станков, которые потребуют наладки в течение часа.

Ответ: 0,3.

28. Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует наладки, равны соответственно: 0,85; 0,9; 0,95. Построить ряд распределения и найти математическое ожидание числа станков, которые не потребуют наладки в течение часа.

Ответ: 2,7.

29. Случайная величина X - эксцентриситет цилиндрической детали подчиняется закону Релея: Р(Х < x) = 1 - ехр(-х² / 2σ²_x), х > 0. Найти плотность вероятности случайной величины X и изобразить ее график.

Ответ: (x/σ²_x)exp(-x²/2σ²_x)

30. Ошибка измерения диаметра цилиндрической детали подчиняется нормальному закону, причем математическое ожидание и среднее квадратичное отклонение равны соответственно 5мкм и 10 мкм. Определить вероятность того, что значение диаметра будет отклоняться по абсолютной величине от истинного не более чем на 15мкм.

Ответ: 0,8187.

31. Случайные ошибки измерения тремя измерительными приборами подчиняются нормальному закону с параметрами: m₁, = 0 , σ₁, = 1 мкм, т₂ = 0 , σ₂ = 2 мкм, т₃ = 0, σ₃ =3мкм. Найти вероятность того, что из трех независимых измерений хотя бы в одном из них ошибка измерения не превзойдет по абсолютной величине 1,5мкм.

Ответ: 0,965.

32. Случайные ошибки измерения подчиняются нормальному закону распределения с параметрами: m=0, σ=1 мкм. Найти вероятность того, что из двух независимых измерений ошибка хотя бы одного из них не превзойдет по абсолютной величине 1,28мкм.

Ответ: 0,96.

33. Агрегаты испытываются независимо на надежность. Известно, что вероятность не выдержать испытания у каждого агрегата одинаковая и равна р. Испытания прекращаются после первого же агрегата, не выдержавшего испытания. Определить математическое ожидание случайного числа агрегатов, выдержавших испытания.

Ответ: (1 - p)/p.

34. Изделия последовательно и независимо испытываются на надежность. Вероятность выдержать испытания у каждого изделия одинаковая и равна р. После первого же изделия, не выдержавшего испытания, они прекращаются. Определить математическое ожидание числа проведенных испытаний.

Ответ: 1/(1 - p).

35. Проводится испытание агрегата, состоящего из двух независимо работающих блоков, вероятности отказа которых соответственно: 0,05; 0,04. Определить математическое ожидание и дисперсию числа блоков, выдержавших испытание.

Ответ: 1,91; 0,7.

36. Испытывается устройство, состоящее из трех независимо работающих блоков. Вероятности отказа блоков следующие: 0,3; 0,4; 0,5. Определить математическое ожидание и дисперсию случайного числа отказавших блоков.

Ответ: 1,2; 0,7.

37. Проводится испытание системы, состоящей из трех независимо работающих элементов. Вероятности отказа этих элементов таковы: 0,3; 0,4; 0,5. Найти математическое ожидание и дисперсию числа элементов, выдержавших испытание.

Ответ: 1,8; 0,7.

38. Проводится испытание системы с четырьмя независимо функционирующими блоками, вероятности отказа которых 0.3; 0,4; 0,5; 0,6. Определить математическое ожидание и дисперсию дискретной случайной величины - числа блоков, выдержавших испытание.

Ответ: 2,2; 0,94.

39. Проводятся независимые испытания трех агрегатов, вероятности отказа которых соответственно равны: р₁,р₂,р₃. Определить математическое ожидание числа агрегатов, выдержавших испытания.

Ответ: 3 – р₁ - р₂ – р₃.

40. Агрегаты испытываются независимо при перегрузочных режимах. Вероятность для каждого агрегата успешно пройти испытания равна 4/5. Испытания останавливаются после первого же агрегата, не выдержавшего испытание. Определить математическое ожидание случайного числа проведенных испытаний.

Ответ: 1,25.

Дата добавления: 2018-08-06; просмотров: 3668; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒

Мы поможем в написании ваших работ!