Два примера применения центральной предельной теоремы.
а) Пусть 
— независимые случайные величины с математическими ожиданиями 
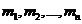и дисперсиями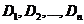 
Предположим, что условия центральной предельной теоремы выполнены и число слагаемых п достаточно для того, чтобы закон распределения величины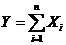 
можно было считать приближенно нормальным.
Тогда вероятность того, что случайная случайная величина У попадает в пределы участка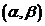 
, выражается фопмулой
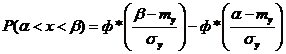
Где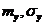 
математическое ожидание и среднее квадратическое отклонение величины V,
Ф* — нормальная функция распределения.
b) Частным случаем центральной предельной теоремы для дискретьых случайных величин является теорема Лапласа.
Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то справедливо соотношение
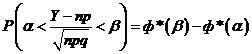
где Y — число появлений события А в n опытах, q = l — р.
Задача 29.6
| xi | 
| 0 | 
|
|
| p1 | 
| 
|
|
Дисперсия 
, поэтому по теореме Чейбыева для попарно независимых случайных величин зедсь выполняется закон больших чисел.
Экзаменационный Билет №5
Независимые и зависимые события.
Событие А называется независимымот события В, если вероятность события А не зависит от того, роизошло событие В или нет.
Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Рассмотрим примеры.
1) Опыт состоит в бросании двух монет; рассматриваются события:
|
|
|
А — появление герба на первой монете,
В — появление герба на второй монете.
В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А независимо от события В.
2) В урне два белых шара и один черный; два лица вынимают из урны по одному шару; рассматриваются события:
А — появление белого шара у 1-го лица,
В — появление белого шара у 2-го лица.
Вероятность события А до того, как известно что-либо о событии В, равна 2/3 Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В.
Следствия закона больших чисел: теорема Бернулли и Пуассона.
Теорема Бернулли.
Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.
Если m число появления события А в n независимых испытаниях с вероятностью успеха в одном испытании p,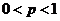 
, то для любого 
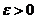справедливо .
Это означает, что с ростом числа испытаний n относительная частота успехов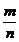 
приближается к вероятности p успеха в одном испытании.
Теорема Пуассона:
Если производится п независимых опытов и вероятность появления события А в i-м опыте равна рi, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей pi.
|
|
|
(Если m – число появления в n независимых испытаниях, но каждое испытание имеет свою вероятность, 
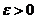, то для любого справедливо ).
Задача 29.9 (а).
неограничена 
не выполняет закон больших чисел (по теореме Чейбышева)
Экзаменационный Билет №6
Формула полной вероятности
Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий: 
образующих полную группу несовместных событий. Будем эти события называть гипотезами.
Докажем, что в этом случае
т. е. вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.
Доказательство.
Так как гипотезы образуют полную группу, то событие A может появиться только в комбинации с какой-либо из этих гипотез: 
Так как гипотезы несовместны, той комбинации 
также несовместны; применяя к ним теорему сложения, получим:
Применяя к событию HiA теорему умножения, получим:
что и требовалось доказать.
Дата добавления: 2018-05-13; просмотров: 260; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!