Критерий устойчивости Михайлова
Критерий был впервые сформулирован А.В. Михайловым в 1938 году. Этот критерий основан на взаимосвязи между характером переходного процесса в системе, возникающего при нарушении равновесия системы, и вынужденными колебаниями, возникающими в системе при наличии синусоидально изменяющихся внешних возмущений. Рассмотрим сущность критерия Михайлова без подробного вывода.
Пусть передаточная функция замкнутой системы автоматического управления 
имеет характеристический многочлен в виде (5.11):
,
где n – порядок системы. Сделаем в нем замену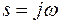 
и получим уравнение некоторого комплексного вектора
. (5.13)
Учитывая, что 
и так далее, можно сгруппировать вещественные и мнимые составляющие друг с другом. В результате выражение (5.13) может быть записано как
, (5.14)
где 
- соответствующие многочлены от 
.
Используем комплексную плоскость, по оси ординат которой будем откладывать значение вещественной части выражения (5.14) 
, а по оси абсцисс – значение мнимой составляющей 
.
Далее, задаваясь различными значениями 
, отмечаем на комплексной плоскости точки с координатами
.
Соединяя эти точки между собой, строим на комплексной плоскости кривую (годограф) Михайлова (рис. 5.9). По характеру годографа Михайлова можно определить устойчивость системы.
Согласно критерию Михайлова линейная система n-го порядка будет устойчива, если кривая Михайлова начинается на положительной (правой) вещественной оси, охватывает начало координат и последовательно проходит n квадрантов плоскости. На рис. 5.9 показаны кривые Михайлова для устойчивых и неустойчивых систем.
|
|
|
Рисунок 5.9 – Кривые Михайлова для устойчивых и неустойчивых систем
Если кривая Михайлова проходит через начало координат, то система находится на границе устойчивости.
Рассмотрим пример определения устойчивости системы с помощью критерия Михайлова. Пусть передаточная функция замкнутой системы автоматического регулирования имеет вид
.
Характеристический многочлен данной передаточной функции запишется как 
. Для построения кривой Михайлова сделаем в нем подстановку :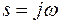
.
Отделяя вещественную часть от мнимой, получим уравнение кривой Михайлова (5.14) , где 
.
Задаваясь различными значениями w от 0 до бесконечности, определяем кривую Михайлова. Для упрощения процесса построения кривой Михайлова целесообразно рассчитать значения координат для первой точки с частотой 
, а затем для характерных точек, когда 
и 
.
При 
. Определим частоту, при которой вещественная часть равна нулю:
.
Для этой частоты значение мнимой части равно
.
Мнимая часть равна нулю при двух значениях частоты: 
и 
. Для последней частоты значение вещественной части равно
|
|
|
.
Сведем все вычисления в таблицу (таблица 5.1).
Таблица 5.1. Координаты кривой Михайлова.
| w | 3,92 | 5,66 | 
| |
| U(w) | -10,82 |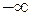 
| ||
| V(w) | 3,26 |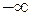
|
В соответствии с табл. 5.1 строим кривую (рис. 5.6). Кривая Михайлова проходит в положительном направлении последовательно три квадранта, следовательно, система устойчива.
Рисунок 5.10 – Кривая Михайлова для таблицы 5.1
Гораздо проще проводить анализ устойчивости систем по критерию Михайлова с помощью программы MathCAD. Для этого достаточно записать характеристический многочлен, определить диапазон изменения частоты, выделить реальную (вещественную) и мнимую части вектора и построить график. На рис. 5.11 приведен пример определения устойчивости системы с помощью программы MathCAD для системы с характеристическим многочленом 
.
Рисунок 5.11 – Пример построения кривой Михайлова с помощью MathCAD
Из графика кривой Михайлова следует, что при порядке характеристического многочлена n = 4 кривая, вместо последовательного прохождения в четырех квадрантах, находится только в двух. Следовательно, рассматриваемая система является неустойчивой.
|
|
|
Дата добавления: 2016-01-04; просмотров: 23; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!