Дифференциальные зависимости при изгибе

⇐ ПредыдущаяСтр 5 из 6Следующая ⇒

Для внутренних силовых факторов при изгибе балки существуют определенные зависимости. Рассмотрим произвольно нагруженную балку (рис. 6.2,а), где положительное направление нагрузкиq(z) совпадает с направлением оси у. Для элементарного участкаdz балки в пределах действия только нагрузкиq учтём возникающие в сечениях внутренние силовые факторы . В пределах малого участка dz нагрузкуq можно считать равномерно распределенной, М и Q приложены в положительном направлении с учётом их изменения по длине.

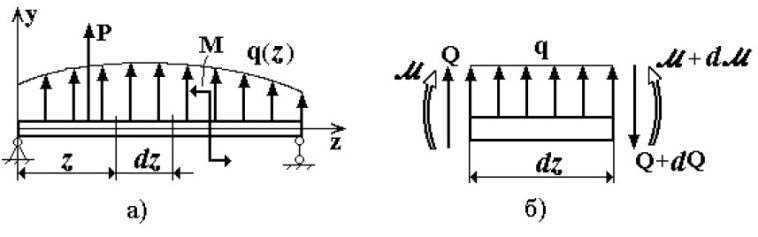
(третье соотношение получено на основе первых двух)

Указанные дифференциальные зависимости при изгибе позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.

1. Для участков, гдеq=0, эпюраQ ограничена горизонтальной прямой, а эпюра М - наклонной прямой (если на участке Q = 0, то М =const).

2. Для участков, гдеq = const ≠ 0, эпюраQ ограничена наклонной прямой, эпюра М - квадратичной параболой.

3. Приq ≠ 0 выпуклость параболической эпюры М противоположна направлению нагрузкиq.

4. В сечении, где Q = 0 приq ≠ 0, эпюра М имеет экстремум: шах - приq< 0, min - приq> 0.

5. В сечении, где приложена внешняя сосредоточенная сила, на эпюреQ имеет место скачок на величину этой силы, а на эпюре М - излом навстречу силе. В сечении, где приложен внешний сосредоточенный момент, на эпюре М имеет место скачок на величину этого момента.

6. Ордината эпюры М численно равна площади эпюрыQ на соответствующем участке (если в пределах этого участка нет сосредоточенных моментов).

Распределение деформации и напряжения в сечении при изгибе

Балка, т.е. стержень, испытывающий изгиб, деформируется таким образом, что первоначально прямая ось балки О₁О₂становится криволинейной; эта ось называется упругой линией (рис. 1.11). Рассмотрим изгиб балки под действием внешней силы F, пренебрегая ее весом. Все волокна, лежащие ниже этой линии, удлиняются (в них возникают растягивающие напряжения), а волокна, лежащие выше этой линии, сжимаются (в них возникают сжимающие напряжения). Между растянутыми волокнами находится нейтральный слой. При этом два, первоначально параллельные сечения и находящиеся на расстоянии dx друг от друга, при изгибе образуют некоторый угол dφέ. Для удобства описания распределения деформации и напряжений свяжем со стержнем систему координат с началом в некоторой точке О упругой линии О₁О₂ и осями x и y, направленными вдоль упругой линии и в поперечном сечении соответственно (см. рис. 1.11). Легко видеть, что деформации в некотором сечении x=const линейно нарастают вдоль оси y от έ1 <0 до έ2>0.

Нормальное напряжение в произвольной точке поперечного сечения

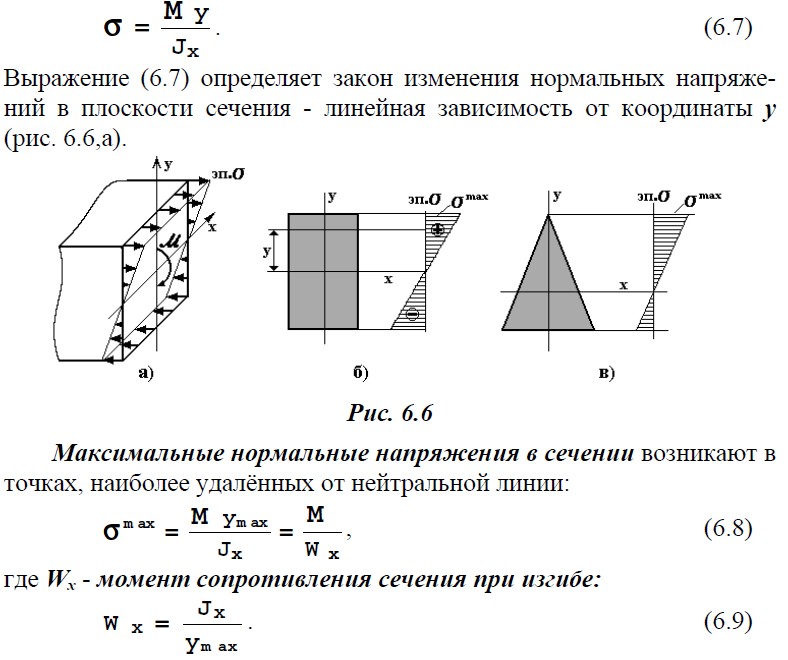
Теории прочности

В реальных условиях элементы конструкций находятся не в условиях чистых «растяжения – сжатия», «кручения», «чистого изгиба» , а тогда, когда если имеет место комбинация этих видов внутренних силовых факторов. Например балки могут находиться в условиях растяжения и кручения одновременно. Либо тоже одновременно кручение изгиба. Если в условиях чистых силовых факторов перечисленных выше, как показано экспериментами вполне достаточно при определении предельных допускаемых нагрузок использовать данную величину dпред, полученную опытным путем при растяжении:

[σ]= σ_пред

То в случае сложных нагружений конструкции этого делать уже нельзя вследствие хотя бы большого разнообразия таких комбинаций. Известно много теорий прочности. Наиболее распространенная – третья и четвертая.

Данные теории основаны на расчете так называемого эквивалентного допускаемого напряжения, которое должно удовлетворить неравенство:

σ_экв ≤ [σ], [σ] – при растяжении

Третья теория прочности (растяжение и сжатие):

По третьей теории прочности Эквивалентное напряжение вычисляют по формуле

В этих формулах — нормальное и касательное напряжения в опасной точке поперечного сечения бруса.

При действии растяжения и кручения в болтах наибольшие значения напряжений определяются по формулам . Подставив эти значения в выражение эквивалентного напряжения, получим условия прочности в следующем виде:

По четвертой теории прочности формула для эквивалентного напряжения имеет несколько иной вид

Третья теория прочности (изгиб+кручение): σ= σ_круч

По третьей теории прочности:

σ_экв= , Wкр=2Wизг

по четвертой теорий прочности

где W — осевой момент сопротивления сечения.

Из приведенных условий прочности для вала вытекают следующие зависимости для определения требуемого момента сопротивления:
по третьей теории прочности:

по четвертой теорий прочности

По найденному значению W и принятому виду сечения (круг или кольцо) вычисляют необходимый диаметр вала. Стоящие в числителях двух последних формул выражения носят название эквивалентных моментов. Формулы для вычисления эквивалентных моментов имеют вид:
по третьей теории прочности:

по четвертой теорий прочности

Максимальный эквивалентный момент:

Мэкв≤ [σ]*W

Дата добавления: 2018-02-18; просмотров: 1026; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 Следующая ⇒

Мы поможем в написании ваших работ!