Задание 7. Производная функции в точке.
1. Найти значение производной функции 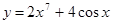 в точке х = 0
в точке х = 0
2. Если 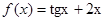 , то
, то  принимает значение, равное …
принимает значение, равное …
3. Найти 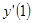 , если
, если 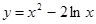 .
.
4. Если  , то
, то 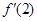 принимает значение, равное …
принимает значение, равное …
5. Если  , то
, то  принимает значение, равное …
принимает значение, равное …
6. Если 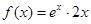 , то
, то  принимает значение, равное …
принимает значение, равное …
Задание 8. Производная сложной функции.
1. 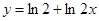 ,
, 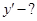
2. 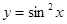 ,
, 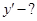
3. 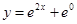 ,
, 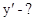
4. 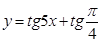 ,
, 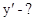
5. Производная функции  равна
равна
6. Производная функции 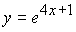 имеет вид …
имеет вид …
7. Найти 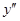 , если
, если  .
.
8. Производная второго порядка функции 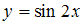 равна …
равна …
Задание 9. Физическое приложение производной.
1. Скорость гоночного автомобиля, движущегося прямолинейно, изменяется по закону 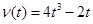 . Ускорение гоночного автомобиля в момент времени
. Ускорение гоночного автомобиля в момент времени 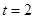 равно …
равно …
2. Скорость точки, движущейся прямолинейно по закону 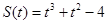 , в момент времени
, в момент времени 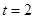 равна …
равна …
3. Ускорение точки, движущейся прямолинейно по закону 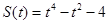 , в момент времени
, в момент времени 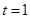 равно …
равно …
4. Зависимость пути от времени при прямолинейном движении точки задана уравнением  . Вычислить ее скорость в момент времени
. Вычислить ее скорость в момент времени 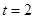 с.
с.
5. Скорость точки, движущейся прямолинейно по закону  , в момент времени
, в момент времени 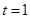 равна …
равна …
6. Скорость гоночного автомобиля, движущегося прямолинейно, изменяется по закону 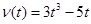 . Ускорение гоночного автомобиля в момент времени
. Ускорение гоночного автомобиля в момент времени 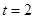 равно …
равно …
Задание 10. Геометрическое приложение производной.
1. Найти угловой коэффициент касательной, проведенной к кривой  в точке
в точке 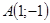 .
.
2. Угловой коэффициент касательной к графику функции 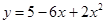 в точке
в точке 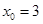 равен …
равен …
3. Укажите абсциссу точки графика функции  , в которой угловой коэффициент касательной равен нулю.
, в которой угловой коэффициент касательной равен нулю.
4. Найти угловой коэффициент касательной, проведенной к кривой 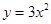 в точке, абсцисса которой равна х=1.
в точке, абсцисса которой равна х=1.
5. Угловой коэффициент касательной к графику функции 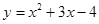 в точке
в точке 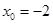 равен …
равен …
Задание 11. Монотонность функции. Точки экстремума.
1. Найти точку максимума функции 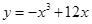 .
.
2. Найти точку максимума функции  .
.
3. Найти точку минимума функции 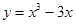 .
.
4. Найти точку минимума функции  .
.
5. Найти промежутки убывания функции 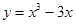 .
.
6. Найти промежутки возрастания функции  .
.
Задание 12. Применение производной в физике.
| 10. | Тело массой 4кг движется прямолинейно по закону | |
| 11. | Тело массой 4кг движется прямолинейно по закону | |
| 12. | Тело массой 4кг движется прямолинейно по закону | |
| 13. | Тело массой 2кг движется прямолинейно по закону | |
| 14. | Тело массой 4кг движется прямолинейно по закону | |
Задание 12. Теоретические вопросы по интегральному исчислению.
| 15. | Если | 1 | неопределенным интегралом |
| 2 | дифференцируемой | ||
| 3 | первообразной | ||
| 4 | интегральной | ||
| 16. | Совокупность всех первообразных функций называется ...? | 1 | первообразной |
| 2 | определенным интегралом | ||
| 3 | неопределенным интегралом | ||
| 4 | дифференциалом | ||
| 17. | Определенный интеграл с равными пределами интегрирования равен … | 1 | единице |
| 2 | нельзя вычислить | ||
| 3 | первообразной функции | ||
| 4 | нулю | ||
| 18. | Формула Ньютона-Лейбница вычисляет … | 1 | определенный интеграл |
| 2 | двойной интеграл | ||
| 3 | неопределенный интеграл | ||
| 4 | табличный интеграл | ||
| 19. | Неверным является … | 1 | 
|
| 2 | 
| ||
| 3 | 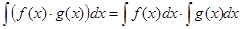
| ||
| 4 | 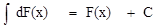
| ||
| 20. | Операция нахождения первообразных по заданному дифференциалу называется … | 1 | дифференцированием |
| 2 | интегрированием | ||
| 3 | потенцированием | ||
| 4 | восстановлением | ||
| 21. | Какая из перечисленных формул является формулой Ньютона-Лейбница? | 1 | 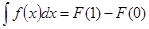
|
| 2 | 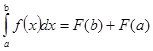
| ||
| 3 | 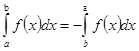
| ||
| 4 | 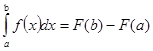
| ||
| 22. | Укажите, какие фигуры на рисунке являются криволинейными трапециями:
| 1 | а, б, в |
| 2 | а | ||
| 3 | г | ||
| 4 | а, г |
Дата добавления: 2021-07-19; просмотров: 79; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 . Определить кинетическую энергию тела
. Определить кинетическую энергию тела  в момент времени
в момент времени  .
.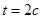 .
. . Определить кинетическую энергию тела
. Определить кинетическую энергию тела 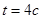 .
.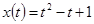 . Определить кинетическую энергию тела
. Определить кинетическую энергию тела  .
.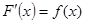 , то функция F(х) называется …?
, то функция F(х) называется …?