Кинематические уравнения для векторов конечных поворотов
Для получения дифференциального уравнения для вектора конечного поворота 
, заданного в виде (7.6), рассмотрим движение координатного трехгранника с базисом 
относительно трехгранника с базисом 
. Пусть в фиксированный момент времени t 12 подвижный базис занимает положение 
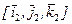, причем ориентация базиса 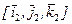относительно базиса определяется вектором конечного поворота
.
В фиксированный момент времени t13 > t12 базис занимает положение 
, причем ориентация базиса относительно базиса определяется вектором конечного поворота
,
а угловое положение базиса относительно базиса 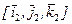определяется вектором конечного поворота
.
Примечание. Далее для упрощения выкладок будем называть базисы , , 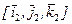базис-1, базис-2, базис-3 соответственно.
Пусть в момент времени t 12 базис имеет угловую скорость 
. Обозначив интервал времени 
, по определению вектора угловой скорости как мгновенной оси вращения запишем:
. (7.33)
Для достаточно малого интервала 
можно записать
.
Для получения выражения для производной
(7.34)
необходимо выразить вектор 
через суперпозицию векторов 
и 
. Для этого запишем связь базисов-1 и -2:
, (7.35)
где 
– соответствующая матрица направляющих косинусов поворота от базиса-1 к базису-2, для которой справедливо (7.19):
.
Запишем связь базисов -2 и -3:
, (7.36)
где 
- матрица направляющих косинусов поворота от базиса-2 к базису-3, для которой с учетом малости угла 
и разложения в ряд
; 
,
формулы (8.30) запишутся в виде:
,
где: О2 – малые величины второго и высших порядков малости.
Выразим связь базисов -1 и -3 с учетом формул (7.35), (7.36):
, (7.37)
где 
- матрица направляющих косинусов поворота от базиса-1 к базису-3:
.
Воспользуемся формулами (7.20) и (7.21) и выразим параметры вектора через элементы матрицы направляющих косинусов (в записанных ниже формулах cij – элементы матрицы ):
; (7.38)
Получим вспомогательные выражения для скалярного, векторного и двойного векторного произведений единичных векторов 
, 
, 
:
;
; (7.39)
Проанализируем первое выражение (7.38) с учетом первой из формул (7.39):
, откуда:
.
Разделим обе части этого уравнения на 
и перейдем к пределу при :
.
Перейдем от предела к производной с учетом (7.33):
,
С другой стороны 
, откуда следует:
. (7.40)
Перепишем оставшиеся три выражения (7.38) в векторном виде с учетом (7.39):
.
Разделим обе части этого уравнения на и перейдем к пределу при :
Перейдем от предела к производной с учетом (7.33):
.
Выполним дифференцирование левой части этого уравнения
,
откуда выразим величину 
:
. (7.41)
Так как 
, то:
и, учитывая формулу (7.8) 
, запишем далее полезные равенства:
и
. (7.42)
Тогда выражение для производной упростится:
. (7.43)
Используя тригонометрическое равенство
,
преобразуем выражение (7.43) к общепринятому виду:
. (7.44)
Выражения (7.42) и (7.43), непосредственно выведенные из определения производной в виде (7.34), являются необходимыми компонентами искомого дифференциального уравнения, для окончательного вывода которого продифференцируем выражение (7.6) для вектора конечного поворота:
. (7.45)
Подставляя в (7.45) полученные выражения (7.42) и (7.43):
.
Учитывая, что 
, окончательно запишем дифференциальное уравнение для вектора конечного поворота:
. (7.46)
Отметим, что полученное уравнение записано в векторном виде и все операции перемножения в правой части проводятся в текущей системе координат.
Обратные уравнения, позволяющие определить вектор угловой скорости по вектору конечного поворота и его производной можно получить, используя (7.40) и (7.44).
Чтобы выразить из (7.44) угловую скорость , следует исключить из него векторные произведения вида 
. Для этого вначале преобразуем двойное векторное произведение в правой части (7.44) по формуле (7.42):
и, подставив его в (7.44), с учетом (7.40) получим:
. (7.47)
Умножим векторно левую и правую части этого уравнения на вектор 
:
. (7.48)
Выразив из (7.47) векторное произведение
и подставим его в (7.48), заменим при этом двойное векторное произведение по (7.42):
Из этого уравнения можно получить выражение вектора угловой скорости в зависимости от вектора конечного поворота и его производной:
. (7.49)
Продифференцировав (7.49), можно получить выражение для углового ускорения 
:
. (7.50)
Дифференциальное уравнение (7.46) при описании кинематики векторов конечных поворотов играет ту же роль, что уравнение Пуассона при описании кинематики матриц направляющих. В качестве примера запишем это уравнение применительно к векторам конечных поворотов 
, 
, 
, которые описывают повороты, соответственно, от Oxyz к OX и Y и Z и, от Oxyz к Oξηζ, от к OX и Y и Z и к Oξηζ:
; (7.51а)
; (7.51б)
, (7.51в)
где – угловая скорость вращения соответствующих трехгранников друг относительно друга.
Дата добавления: 2021-01-21; просмотров: 194; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!