Показатели ремонтнопригодности

К показателям ремонтопригодности относятся:

Вероятность восстановления и среднее время ремонта.

Вероятность восстановления работоспособности в заданное время t определяетсяпо формуле:

где — плотность распределения времени восстановления.

Если через п ( t) обозначить число восстанавливаемых изделий и через N— число работоспособных изделий, при статистической оценке

Показателисохраняемости

К показателям сохраняемости (при хранении или транспортировке изделий) относятся безотказности при хранении и средний срок сохраняемости за промежуток времени от t₁ до t₂:

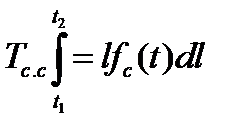где f_o( t)—плотность распределения работоспособности при хранении.

Комплексные показатели готовности изделий

Существуют комплексные показатели готовности изделий.

К ним относятся коэффициент готовности и коэффициент технического использования.

Коэффициент готовности характеризует вероятность работоспособности изделия в произвольный момент времени

K _Г = T ₀ /( T ₀ + Tc ),

где T ₀ — наработка на отказ, Т_с — среднее время восстановления.

Коэффициент технического использования

Т_Т.И = t _сум /( t _сум + t_p + t _об ).

Здесь t _сум — суммарная наработка; t_p — суммарный простой в плановых и неплановых ремонтах, t _об — суммарное время простоя в техническом обслуживании.

Показатели, используемые в автомобильном транспорте

На автомобильном транспорте применяются такие коэффициенты: технической готовности, выпуска подвижного состава и использования парка.

Коэффициент технической готовности

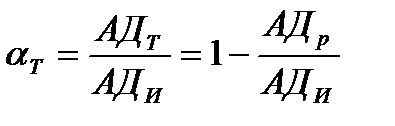где АД_Т — автомобиле – дни нахождения автомобилей в технически исправном состоянии; АД_И– автомобиле – дни инвентарные; АД_р – автомобиле – дни нахождения в ремонте (обязательные работы, диагностирование, устранение неисправностей).

Коэффициент выпуска подвижного состава

где АД_Э – автомобиле-дни нахождения в эксплуатации; АД_Н – автомобиле-дни нормированных простоев (число выходных и праздничных дней, в которые парк не работает).

Коэффициент использования парка

Лекция4.Статистические и функциональные методы определения параметров и причин отказов .

4.1.Статистические параметры распределения. Среднее арифметическое, мода, медиана, математическое ожидание.

4.2.Меры рассеивания в параметрах распределения случайных величин.

4.3.Показатели надежности как случайные величины. Дискретные и непрерывные случайные величины.

4.4.Сбор статистической информации о надежности объектов. Методика обработки полной информации. Математические методы расчетов показателей надежности.

4.5.Порядок задания законов распределения функциями распределения. Дискретная, интегральная и дифференциальная функция распределения и их физическая сущность.

Характеристики (параметры) распределения случайных величин. Числовые характеристики, подсчитанные по полученным значениям в процессе испытания или опыта случайной величины называют статистическими характеристиками. Характеристики, определенные по теоретическим законам распределения, называются параметрами распределения.

Основными статистическими характеристиками случайных величин, изучаемых в теории надежности, служат среднее арифметическое и среднее квадратическое отклонения.

Среднее арифметическое — это частное от деления суммы измеренных значений на число слагаемых этой суммы, т. е. на число испытаний (опытов):

(3.7)

где - среднее арифметическое из N испытаний; x₁, x₂, … , x_n – отдельные измеренные значения наблюденной величины; N – число проведенных испытаний.

В том случае, когда среди полученных значений случайных величин имеются одинаковые, несколько раз повторяющиеся с определенной частотой, их среднее значение называется средней взвешенной.

Средняя взвешенная величина определяется по формуле:

(3.8)

Тогда

(3.9)

Для упрощения среднюю взвешенную очень часто подсчитывают по следующей формуле:

(3.10)

где А – произвольное число, которое подбирают так, чтобы разности (x_i – A) были возможно простыми и малыми числами.

Обычно А выбирают приблизительно равным среднему значению случайной величины на глаз или равным значению, соответствующему наибольшей частоте значений случайной величины в ряду распределения.

Из формулы (3.10) следует, то средняя взвешенная подсчитывается как сумма произведений значений случайной величины Хг на соответствующие им частости mi/ N, т. е.

(3.11)

При достаточно большом числе испытаний частности приближенно равны соответствующей вероятности:

Заменив в формуле (3.11) относительные частоты соответствующими вероятностями,

(3.12)

получим для дискретной случайной величины равенство для определения математического ожидания:

Математическое ожидание дискретной случайной величины, подсчитанное по заданному закону распределения, называется суммой парных произведений возможных значений случайной величины х\

на соответствующие им вероятности Pi.

Для непрерывной случайной величины:

(3.13)

Среднее значение характеризует центр группирования значений случайной величины. При N^- oo величина X стремится по значению к математическому ожиданию, т. е. Хх MX.

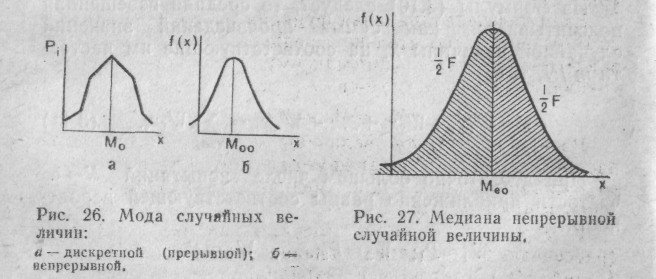
Мода М„ эмпирической совокупности — это значение прерывной случайной величины Xi, соответствующее наибольшей ординате полигона распределения (рис. 26,а). За

моду прерывной случайной величины принимают значение, имеющее наибольшую вероятность.

Мода Моо теоретического распределе мяльному значению плотности распределения f( x) (рис. 26, б).

Модой также называется значение признака, встречающееся с наибольшей частотой, т. е. значение приз-нака, наиболее типичное в данном статистическом ряду.

Медиана М _е или срединное значение эмпирической совокупности — это такое зафиксированное значение случайной величины Xi, которое .является срединным членом (объектом) в ряде значений, упорядоченных по их возрастанию или убыванию.

Другими словами, медианой называется значение признака, относительно которого эмпирическая совокупность делится на две равные по числу членов части

Медиана М_ео теоретического распределения случайной в е л и ч и н ы — это такое значение xt, при котором вероятность появления величин х, меньших Мео, равна вероятности появления величин X, больших М_ео,

Ордината кривой распределения, соответствующая значению случайной величины х=М_во, делит площадь под кривой распределения на две равные части (рис. 27).

Если дифференциальная функция распределения f( x) симметрична относительно среднего арифметического значения X и имеет один максимум, то мода и медиана совпадают с математическим ожиданием, т. е.

Разброс случайной величины относительно центра распределения (среднеарифметической, математического ожидания, моды или медианы) характеризуется мерами рассеивания.

К мерам рассеивания относятся: размах, дисперсия (рассеивание), среднее квадратическое отклонение (стандарт) и коэффициент вариации.

Дата добавления: 2019-09-08; просмотров: 332; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!