Методы хранения и обработки информации
Источниками и носителями информации могут быть сигналы любой природы: речь, музыка, текст, показания приборов и т. д.
Хранение информации осуществляется на долговременных носителях. Это могут быть камень, пергамент, кожа, бумага, магнитные носители, лазерные диски, серверы вычислительных сетей и т. п. Однако хранение, передача и переработка информации в ее естественном (физическом) виде большей частью неудобны, а иногда и просто невозможны. В таких случаях применяется кодирование.
Кодирование – это процесс установления взаимно однозначного соответствия элементам и словам одного алфавита элементов и слов другого алфавита. Кодом называется правило, по которому сопоставляются различные алфавиты и слова (отображение и преобразование информации в вид, удобный для человеческого восприятия, см. на рис. 3).

Рис. 3. Отображение и преобразование информации
Всю информацию, участвующую в этом процессе, можно разделить на обрабатываемую (ее называют данными) и управляющую (в применении к вычислительным процессам ее называют программами).
Системы счисления и области их использования
Системой счисления называется способ записи чисел.
Позиционной системой счисления называется система счисления, при которой число, связанное с цифрой, зависит от места, которое оно занимает. Место числа называют его разрядом в записи числа. Примером могут служить десятичная и шестидесятеричная системы счисления.
|
|
|
Непозиционной системой счисления является та система, в которой порядок записи числа, связанного с цифрой, не зависит от места, которое оно занимает. Примером может служить римская система записи чисел.
Представление чисел в различных системах счисления. Под основанием системы счисления р будем понимать число используемых в ней символов – цифр. В десятичной системе р = 10 и для построения чисел используются десять цифр: 0, 1, 2…, 9. Число представляется в виде последовательности цифр, разделенных запятой на две группы: одна группа (левее запятой) образует целую часть, другая (правее запятой) – дробную. Каждая цифра числа занимает определенную позицию – разряд. Разрядам приписываются различные весовые коэффициенты. Эти коэффициенты для разрядов влево от запятой равны соответственно 100, 101, 102…, 10n; вправо от запятой – 10‑1, 10‑2…, 10‑n.
Таким образом, запись 547,359 в десятичной системе счисления означает величину:

В общем случае изображение некоторого числа N имеет вид апап‑1… а1a0 а‑1а‑2… а‑т. Здесь ап, ап‑1…, а‑т – последовательность цифр, соответствующих п, n‑1…, п‑т разрядам.
|
|
|
При основании системы счисления р запись числа N соответствует следующей величине:

Здесь рп, рп‑1, …, р‑т – весовые коэффициенты соответствующих разрядов. В качестве цифр разрядов используются символы, обозначающие положительные целые числа, меньшие р (0 ≤ aj ≤ р‑1). Используя такой позиционный принцип представления чисел, можно строить разнообразные системы счисления, задаваясь различными значениями основания системы р. Рассмотрим некоторые наиболее употребительные системы счисления.
Двоичная система счисления (р = 2). Для представления цифр разрядов используются лишь два символа: 0 и 1.
Например:
число 11010,112 соответствует следующей величине:

где нижние индексы показывают основание системы счисления, в которой представляется число.
Весовые коэффициенты разрядов, отсчитываемых влево от запятой (в целой части числа), равны соответственно 1, 2, 4, 8, 16…, а весовые коэффициенты разрядов вправо от запятой (в дробной части числа) –

Восьмеричная система счисления (р = 8). Для представления цифр разрядов используют восемь символов: 0, 1, 2, 3, 4, 5, 6, 7. Например, запись числа 756,258 в этой системе счисления соответствует следующей величине:

Весовые коэффициенты разрядов в целой части – 1, 8, 64…, в дробной части – 1/8, 1/64.
|
|
|
Шестнадцатеричная система счисления (р = 16). Цифры разрядов изображаются шестнадцатью символами: 0, 1, 2…, 9, A, B, C, D, E, F.
Десять символов заимствованы из десятичной системы, а в качестве недостающих шести символов использованы буквы А, В, С, D, Е, F, которым в десятичной системе соответствуют числа 10, 11, 12, 13, 14, 15.
Например:
запись А7В, С816 соответствует следующей величине:

Хранение n‑разрядных чисел. Хранение осуществляется с помощью устройств, содержащих п элементов, каждый из которых запоминает соответствующую цифру числа. Наиболее просто осуществляется хранение чисел, представленных в двоичной системе счисления. Для запоминания цифры каждого разряда двоичного числа используются устройства с двумя устойчивыми состояниями, такие, как триггеры. Одному из этих состояний ставится в соответствие цифра 0, другому – цифра 1.
При хранении десятичных чисел каждая цифра десятичного числа предварительно представляется в двоичной форме. Такая форма представления десятичных чисел носит название двоично‑кодированной десятичной системы.
Например, число 735,8210 в двоично‑кодированной десятичной системе может быть представлено в следующем виде:
|
|
|

Несмотря на внешнее сходство с двоичным числом, двоично‑кодированное десятичное число (содержащее лишь цифры 0 и 1) не является двоичным. Например, если целую часть приведенной выше записи рассматривать как двоичное число, то оно при переводе в десятичную форму означало бы 184510, что не совпадает с целой частью исходного числа 735.
Рассмотренный способ двоичного представления (кодирования) десятичных цифр использует код 8421 (название кода составлено из весовых коэффициентов разрядов двоичного числа). Наряду с этим кодом при двоичном кодировании десятичных цифр используются и другие коды, наиболее употребительные из которых приведены в табл. 1.
Эти коды имеют следующие особенности:
код 8421 является естественным представлением десятичных цифр в двоичной системе счисления;
код 7421 интересен тем, что любая кодовая комбинация содержит не более двух единиц;
в коде 2 из 5 все кодовые комбинации содержат точно две единицы. Это свойство используется для обнаружения ошибочных комбинаций (ошибочное распознавание любого из символов принятой кодовой комбинации изменяет число единиц, благодаря чему достигается возможность выявления таких ошибочных комбинаций).
Таблица 1. Наиболее употребительные коды в двоично‑кодированной десятичной системе счисления

Пары десятичных цифр, сумма которых равна девяти, составляют цифры, взаимно дополняющие друг друга до девяти (0 и 9, 1 и 8, 2 и 7…).
В коде 2421 и коде с избытком 3 кодовая комбинация, соответствующая любой из десятичных цифр, представляет собой инверсию комбинации, соответствующей ее дополнению до девяти. Например, в коде 2421 паре взаимно дополняющих до девяти цифр 2 и 7 соответствуют комбинации 0010 и 1101, каждая из которых образуется как инверсия другой. Это свойство упрощает выполнение в цифровых устройствах арифметических операций над десятичными числами. Таким же свойством дополнения до девяти обладает код За + 2. Кроме того, этот код имеет и другое полезное свойство: любая пара кодовых комбинаций отличается не менее чем в двух разрядах, что позволяет обнаружить ошибочные комбинации (ошибка, изменяющая цифру одного разряда любой из кодовых комбинаций, приводит к так называемой запрещенной комбинации, не используемой для представления десятичных цифр).
Перевод чисел из одной системы счисления в другую. Перевод чисел из десятичной в двоичную систему счисления. Для перевода десятичного числа в двоичную систему счисления отдельно выполним операции перевода для целой и дробной частей. Для небольших чисел можно воспользоваться таблицей целых степеней числа 2 (табл. 2).
Таблица 2. Степени числа 2

Целая часть. Осуществляем последовательное деление целой части на основание системы счисления (2) с записью остатков. Двоичное число считывается от последнего результата по остаткам (от последнего остатка к первому).
Пример.
Целое десятичное число 87 переведем в двоичную систему счисления.

Для проверки просуммируем вес разрядов двоичного числа:
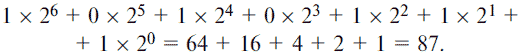
Дробная часть. Дробную часть десятичного числа будем последовательно умножать на 2, исключая из промежуточных результатов целую часть и записывая ее в разряды двоичного числа после запятой. Если точный ответ не получается за несколько шагов, т. е. получается бесконечная непериодическая последовательность, то вычисления проводятся до достижения требуемой точности результата (до определенного числа знаков после запятой).
Пример.
Десятичные дроби 0,3125 и 0,7163 переведем в двоичную форму:

В первом случае получен точный результат:

Во втором случае вычисления проводились с точностью до семи знаков после запятой. Обратите внимание, что все получаемые разряды дробной части числа записываются после запятой в том порядке, в котором они получены.
Перевод чисел из двоичной системы счисления в десятичную. Перевод двоичных чисел в десятичную систему счисления осуществляется с помощью целых степеней числа 2 (табл. 2). Суммируем вес разрядов двоичного числа, в которых стоят единицы. Там, где в числе стоит 0, соответствующий вес разряда умножен на 0 и суммировать нечего.
Пример.

Аналогично число можно перевести из любой другой системы счисления в десятичную, просуммировав вес его разрядов, умноженный на цифры числа.
Перевод чисел в кратных системах счисления. Основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью двух (8 = 23; 16 = 24). Этим объясняется простота преобразования чисел, представленных в этих системах, в двоичную систему счисления и обратно. Каждая восьмеричная цифра для получения ее двоичного представления требует три двоичных разряда, а шестнадцатеричная – четыре.
Двоичная запись цифр различных систем счисления приведена в табл. 3.
Таблица 3. Сравнение значений кодов в различных системах счисления

Для перевода чисел из восьмеричной системы счисления в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом – триадой.
Например:

Перевод шестнадцатеричных чисел в двоичную систему счисления достигается представлением цифр шестнадцатеричного числа четырехразрядными двоичными числами – тетрадами.
Например:
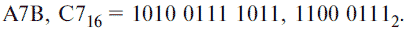
При обратном переводе чисел из двоичной системы в восьмеричную или шестнадцатеричную системы счисления необходимо разряды двоичного числа, отсчитывая их от запятой влево и вправо, разбить на группы по три разряда – в случае перевода в восьмеричную систему, или на группы по четыре разряда – в случае перевода в шестнадцатеричную систему счисления. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представляется цифрой той системы счисления, в которую переводится число.
Например:

Для перевода числа из шестнадцатеричной системы счисления в восьмеричную надо записать двоичное представление числа, разбить двоичные разряды на триады вправо и влево от запятой, дополняя недостающие нули слева от целой части и справа от дробной, и прочесть восьмеричное число, соответствующее триадам.
Пример.
Число EF2C,1D переведем в восьмеричную систему счисления.
Запишем двоичную форму числа, последовательно записав тетрадами его шестнадцатеричные цифры:

Сгруппируем двоичные разряды числа в триады вправо и влево от запятой:

Недостающие нули записаны перед целой частью и после дробной части. Восьмеричное число получаем, записывая последовательно восьмеричные цифры, соответствующие двоичным триадам: 167454,0728.
Перевод восьмеричного числа в шестнадцатеричную систему счисления осуществляется в обратном порядке: запись двоичной формы числа триадами, группировка двоичных разрядов в тетрады вправо и влево от запятой с дополнением нулей слева от целой части и справа от дробной, считывание шестнадцатеричного результата в соответствии с тетрадами.
Пример.
Число 563,418 переведем в шестнадцатеричную систему счисления.
Запишем двоичную форму числа, последовательно записав двоичными триадами его восьмеричные цифры: 563,418 = 101 110 011, 100 0012. Сгруппируем двоичные разряды числа в тетрады вправо и влево от запятой: 0001 0111 0011, 1000 0100 (недостающие нули записаны перед целой частью и после дробной). Шестнадцатеричное число получаем, записывая последовательно шестнадцатеричные цифры, соответствующие двоичным тетрадам: 173,8416.
Арифметические операции в двоичной системе счисления. Основной операцией, которая используется в цифровых устройствах при выполнении различных арифметических действий, является алгебраическое сложение (сложение, в котором могут участвовать как положительные, так и отрицательные числа). Вычитание легко сводится к сложению путем изменения знака вычитаемого на обратный. Операции умножения и деления также сводятся к сложению и некоторым логическим действиям. Поэтому именно с операции сложения начнем рассмотрение способов выполнения арифметических операций.
При записи кода числа будем знак числа представлять заключаемыми в скобки цифрами: (0) – для положительных чисел и (1) – для отрицательных. Именно так в устройствах, предназначенных для хранения чисел, принято фиксировать знак числа в специально выделяемых знаковых разрядах регистра флагов. Положение запятой в числе показывать не будем.
Сложение положительных чисел покажем на примере:

Цифры разрядов суммы N = N1 + N2 формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом, кроме цифры разряда суммы, формируется цифра переноса в следующий, более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.
Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше р = 2 (р – основание системы счисления). При этом в разряд суммы заносится цифра, на р единиц (т. е. на 2) меньшая результата суммирования.
Алгебраическое сложение с использованием дополнительного кода. Для пояснения сущности излагаемого метода рассмотрим следующий пример. Пусть требуется сложить два десятичных числа N1 = (0)831 и N2 = (1)376. Так как второе слагаемое – отрицательное число, то использование приема, предлагаемого в школьной программе, потребовало бы последовательности действий с займами из старших разрядов. Предусматривать в цифровом устройстве дополнительно такую последовательность действий необязательно. Искомый результат может быть получен и при использовании последовательности действий с передачей переносов в старшие разряды, которая применяется при сложении положительных чисел. Для этого достаточно отрицательное число (1)376 предварительно преобразовать в так называемый дополнительный код следующим образом: во всех разрядах, кроме знакового, запишем дополнение до девяти к цифрам этих разрядов и затем прибавим единицу в младший разряд. Дополнительный код для числа N2 = (1)376 есть N2ДОП = (1)624.
Далее произведем сложение по правилам сложения положительных чисел. Единицы переноса показаны там, где они суммируются, а не в тех столбцах, откуда перенос осуществлен:

При сложении складываются и цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Как видим, получен правильный результат (действительно, 831 – 376 = 455).
В двоичной системе счисления дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (путем замены 0 на 1 и 1 на 0) цифры всех разрядов, кроме знакового, после чего в младший разряд прибавляется единица. Например, если N = (1)10110, то NДОП = (1)01010. Обратное преобразование отрицательных чисел из дополнительного кода в прямой производится по тому же правилу.
Рассмотрим примеры выполнения операции.
Пример.
Пусть N1 = (0)10110; N2 = (1)01101; N2ДОП = (1)10011.

Как указывалось выше, перенос, возникающий из знакового разряда, отбрасывается.
Пример. Изменим на обратные знаки слагаемых, использованных в предыдущем примере: N1 = (1)10110; N2 = (0)01101. Очевидно, ожидаемый ответ: N = N1 + N2 = (1)01001.

Таким образом, если результат сложения – отрицательное число, то оно оказывается представленным в дополнительном коде.
Алгебраическое сложение с использованием обратного кода. Вместо дополнительного кода для представления отрицательных слагаемых может быть использован обратный код. Обратный код отрицательных двоичных чисел формируется по следующему правилу: цифры всех разрядов, кроме знакового, инвертируются. Обратное преобразование из обратного кода в прямой производится по тому же правилу.
Рассмотрим те же примеры, используя обратный код:

При использовании обратного кода перенос, возникающий из знакового разряда, прибавляется в младший разряд суммы.

Если результат сложения – отрицательное число, оно оказывается представленным в обратном коде.
Использование модифицированного кода. Особенность модифицированного кода состоит в том, что в нем предусматривается два знаковых разряда. В обоих знаковых разрядах положительные числа содержат нули, отрицательные – единицы.
Выполнение операции суммирования с использованием модифицированного дополнительного или модифицированного обратного кода производится по правилам, сформулированным выше. Если результат суммирования содержит в знаковых разрядах комбинацию 01 или 10, это служит признаком так называемого переполнения разрядной сетки. Переполнение разрядной сетки – явление, при котором результат операции содержит большее число разрядов, чем число разрядов в устройстве, предназначенном для его хранения. При этом некоторые разряды результата не могут быть зарегистрированы в устройстве; они теряются, и результат оказывается ошибочным.
Пример.
Пусть N1 = (0)(0)11011; N2 = (1)(1)10101.
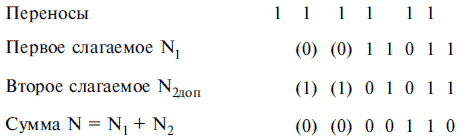
Пример.
Пусть N1 = (0)(0)10110; N2 = (0)(0)11011.
Комбинация цифр (0)(1) в знаковых разрядах результата суммирования свидетельствует о переполнении разрядной сетки; зафиксированный результат ошибочен. Ошибка связана с тем, что при суммировании перенос из старшего разряда оказался зафиксированным во втором из знаковых разрядов. Для регистрации результата суммирования в данном примере требуется шесть разрядов (без учета знаковых разрядов).
Пример.
Пусть N1 = (1)(1)101101; N2 = (1)(1)011101.

И в этом случае комбинация цифр (1)(0) в знаковых разрядах сигнализирует о переполнении разрядной сетки. Для регистрации результата без учета знаковых разрядов в данном примере требуется семь разрядов, и в отведенных для него шести разрядах он не помещается.
Дата добавления: 2018-10-26; просмотров: 605; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
