Задача 3 ( для самостоятельного решения).
Найти легко: точка, в которой они пересекаются на чертеже, и есть изображение их точки пересечения в пространстве.
Параллельное проецирование
Если известны параллельные проекции А1, В1
Точек А и В на данную плоскость а, то найдем точку пересечения прямых А В и А1 В1. Это и будет искомая точка пересечения прямой АВ и плоскости а.
Центральное проецирование
Пересечение прямой АВ и плоскости α легко найти, если даны точки А1, В1 пересечения с плоскостью а двух пересекающихся прямых, проходящих через точки А и В соответственно
Построение сечений пирамиды
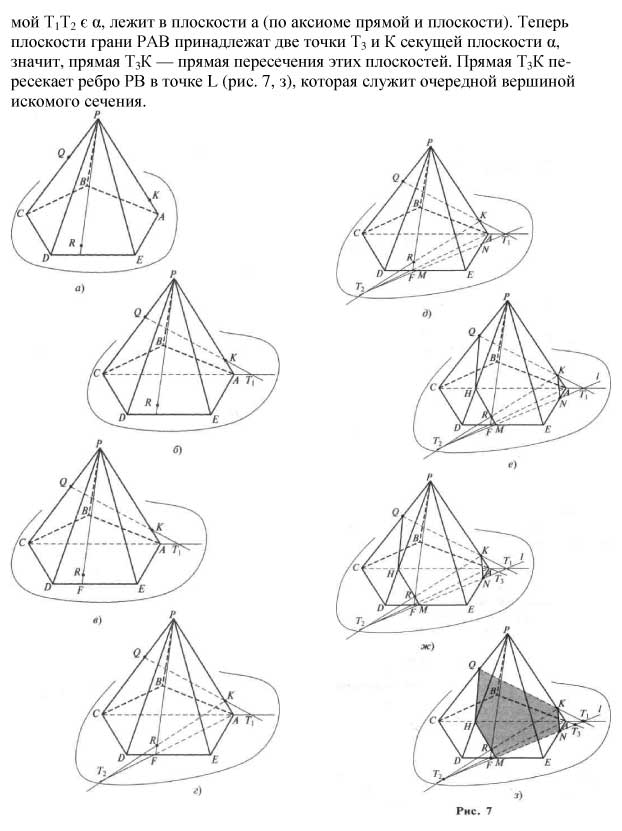
Задача №1: Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через точки: MÎSB, NÎSC,KÎAD.
Построение:
1) Так как точки M и N принадлежат одной грани BSC, соединим эти точки. Прямая MN пересекает ребро BC в точке X;
2) Так как точки X и K лежат в плоскости основания ABCD, соединим эти точки. Прямая XK пересекает ребро DC в точке P и реброAB в точке Y соответственно;
3) Так как точки Y и M лежат в плоскости грани ABS, соединим эти точки. Прямая YM пересекает ребро SA в точке Q;
4) Соединим последовательно точки Q, M, N, P, K. Получим искомое сечение MNPKQ.
Анимация построения:
Задача №2: Построить сечение пирамиды ABCDS, проходящее через точки X, Z, Y на гранях ABS, CBS и ребре BS соответственно.
Построение:
1) Так как точки Y и Z лежат в плоскости грани SBC, соединим эти точки. Прямая YZ пересекает ребра BC и SC в точках C' и Z' соответственно;
2) Так как точки X и Y лежат в плоскости грани ABS, соединим эти точки. Прямая XY пересекает ребра AB и SA в точках A' и X' соответственно;
3) Так как точки A' и C' лежат в плоскости основания ABCD, соединим эти точки. Прямая A'C' пересекает ребра AD и CD в точках D' и B' соответственно;
Соединим последовательно точки Y, X', D', B', Z'. Получим искомое сечение YX'D'B'Z'.
Анимация построения:
|
Комментарии
|
|
|
У вас нет прав для добавления комментариев.
· Пикулева Наталья Львовна, завуч, учитель математики
Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.
Данный материал характеризуется следующим особенностями:
1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
2. В задачах используются в основном простейшие многогранники.
3. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.
Чтобы решить задачу построения сечения многогранника ученик должен знать:
|
|
|
· что значит построить сечение многогранника плоскостью;
· как могут располагаться относительно друг друга многогранник и плоскость;
· как задается плоскость;
· когда задача на построение сечения многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
· тремя точками;
· прямой и точкой;
· двумя параллельными прямыми;
· двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
Существует три основных метода построения сечений многогранников:
1. Метод следов.
2. Метод вспомогательных сечений.
3. Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического метода построения сечений.
Можно также выделить следующие методы построения сечений многогранников:
· построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
· построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
· построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
|
|
|
· построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
· построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.
В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:
· Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
· Погорелова А.В. (Геометрия, 7-11);
· Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
· Смирновой И.М. (Геометрия, 10-11);
· Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.
|
|
|
Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.
Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:
1. Определение сечения многогранников.
2. Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
3. Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
4. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.
(система уроков и факультативных занятий по теме “Построение сечений многогранников”)
УРОК 1.
Тема урока: “Построение сечений многогранников”.
Цель урока: ознакомление с методами построений сечений многогранников.
Этапы урока:
1. Актуализация опорных знаний.
2. Постановка задачи.
3. Изучение нового материала:
А) Определение сечения.
Б) Методы построений сечений:
а) метод следов;
б) метод вспомогательных сечений;
в) комбинированный метод.
4. Закрепление материала.
Примеры построений сечений методом следов.
5. Подведение итогов урока.
Тест.
Ход урока.
Актуализация опорных знаний.
Вспомним:
- пересечение прямой с плоскостью;
- пересечение плоскостей;
- свойства параллельных плоскостей.
Постановка задачи.
Изучение нового материала.
А) Итак, задача состоит в построении пересечения двух фигур: многогранника и плоскости ( рис.1). Это могут быть: пустая фигура (а), точка (б), отрезок (в), многоугольник (г). Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.
Рис. 1
Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.
Исследуйте сечения куба (рис.2) и ответьте на следующие вопросы:
Рис. 2
- какие многоугольники получаются в сечении куба плоскостью? (Важно число сторон многоугольника);
[ Предполагаемые ответы: треугольник, четырехугольник, пятиугольник, шестиугольник.]
- может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные сечения плоскостью ( на модели). Какие многоугольники получаются?
Какой можно сделать вывод? Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?
[ Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.]
Б) а) Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.
б) Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического метода построения сечений многогранников плоскостью.
в) Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
А теперь на примере решения задач рассмотрим метод следов.
Закрепление материала.
Задача 1.
Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже (рис.3)).
Решение.
Рис. 3
1. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
2. Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S1, принадлежащую следу.
3. Аналогично получаем точку S2 пересечением прямых QR и BC.
4. Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы.
5. Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D. Аналогично получаем TU и RT.
6. PQRTU – искомое сечение.
Задача 2.
Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.4)).
Решение.
Рис. 4
1. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проодящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
2. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
3. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х.
4. Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN.
5. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP. Эта прямая пересечет сторону В1С1 в точке Y.
6. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.
Задача 3 ( для самостоятельного решения).
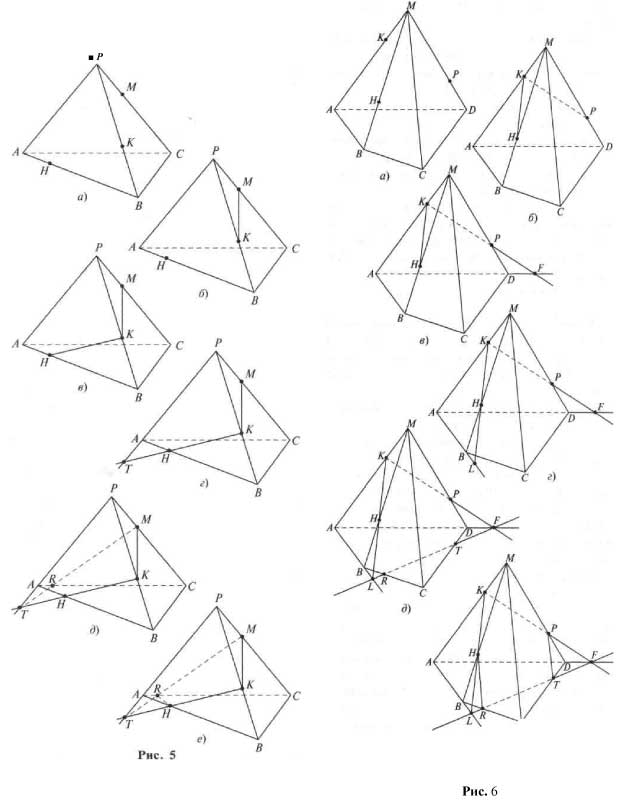
Построить сечение тетраэдра DACB плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.5)).
Рис. 5
Подведение итогов урока.
Ответьте на вопрос: являются ли закрашенные фигуры сечениями изображенных многогранников плоскостью PQR? И выполните правильное построение (рис. 6).
Вариант 1.
а)
б)
в)
г)
д)
Вариант 2.
УРОК 2.
Дата добавления: 2018-06-01; просмотров: 891; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!