Производящие функции и их свойства.
Опр.Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,… Таким образом, если случайная величина Х—целочисленная, то она имеет ряд распределения
| Х | 0 | 1 | 2 | … |
| Р | р0 | р1 | р2 | … |
Опр.Пусть Х—целочисленная величина, ее производящей функцией называется функция 
Свойства производящих функций.
Свойство 1.Производящая функция 
определена в области 
.
Свойство 2.Производящая функция 
Свойство 3.Значение производящей функции в точке Z=1, P(1)=1. Док- во: 
.
Свойство 4. Если Z=1, то MX=P’(1)
Характеристические функции и их свойства.
Опр1 Случайная величина 
, где i—мнимая единица, а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной.
Опр2Математическим ожиданием комплекснозначной случайной величины Z называется 
. Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин.
Опр3 Комплекснозначные случайные величины Z1=X1+iY1 и Z2=X2+iY2 называются независимыми, если независимы соответственно 
.
Свойство комплекснозначных случайных величин.
Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е. 
.
Опр4 Характеристической функцией случайной величины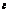 
называется функция 
.
|
|
|
Формулы для вычисления характеристической функции.
Случай 1. Пусть 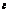—дискретная случайная величина с рядом распределения
|
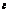
| x1 | x2 | … |
| Р | p1 | p2 | … |
.
Случай 2. Пусть 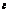—целочисленная случайная величина с плотностью 
. Тогда характеристическая функция 
.
Свойства характеристических функций.
Свойство 1.Характеристическая функция определена для любой случайной величины. При этом 
, 
.
Док-во: 
. 
. Поскольку 
, то 
Закон больших чисел в форме Чебышева и Бернулли.
Опр1. Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если 
при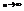 
. Обозначается 
.
Опр2. Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если 
.
Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство Чебышёва:
Для . 
.
Док-во: 
.
Таким образом, 
, 
.
Теорема 2. (закон больших чисел в форме Чебышёва).
Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. 
. Тогда эта последовательность удовлетворяет закону больших чисел.
|
|
|
Док-во: Обозначим через 
. Нужно доказать, что 
. 
.
Центральная предельная теорема.
Теорема. (Ц.П.Т.).Пусть Х1,Х2,…—последовательность независимых случайных величин, имеющих один и тот же закон распределения и конечное математическое ожидание а и дисперсию G2. Тогда при 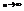вероятность того, что 
, где 
. N(x)—функция стандартного нормального распределения.
Замечание 1. Центральная предельная теорема обосновывает тот факт, что нормальное распределение встречается в природе чаще других.
Док-во: 
. 
.
Свойство 5. 
Док-во: 
. Если Z=1 
.
.
Следовательно, 
.
Свойство 6.Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая функция 
.
Док-во: 
.
Свойство 2.Характеристическая функция случайной величины 
, где a, b—некоторые числа. 
.
Док-во: 
.
Свойство 3.Если случайные величины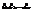 
—независимы, то характеристическая функция суммы данных случайных величин равна произведению характеристических функций этих случайных величин, т.е. 
.
Свойство 4.Если М 
, характеристическая функция случайной величины 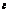n раз дифференцируема, причем 
, где 
.
Отсюда 
(т.к. 
).
Дата добавления: 2018-05-13; просмотров: 868; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!