Функції від матриць. Подання розв’язку стаціон. і нестаціон. лінійних систем керування через фундаментальний р – ок.
(1)- нестац. лін.система x(t) є R 
, x є R u(t) є R 
, 
, 
– відомі.
(1.1)– стаціон. лін.система.
(2)
Лема: Ряд (2)збіг. абсолютно при кожному фікс. tдля дов. квадратної матр. А з дійсними або комплексними елементами і рівномірно на будь-якому скінченому інтервалі.
(3)
Теорема: Якщо матриця 
задовольняє умови леми 4.1, то розв’язок матричної задачі Коші
(4)
має вигляд
(5)
Твердження1:
Розглянемо таку задачу
(7), 
(8)
Розв’язком є вектор 
.
Теорема 4.3 Якщо матриця задовольняє умови леми 4.1, то розв’язок задачі
(9)
має вигляд
. (10)
Доведення цієї теореми одержується безпосередньою перевіркою.
В рівності (10) покладемо всі компоненти вектора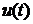 
рівними нулеві, за винятком однієї 
( 
), яку візьмемо рівною одиничному імпульсу 
, зосередженому в точці 
. Позначимо 
розв’язок рівняння (0) за умови 
. Одержимо
– 
-й рядок.
Подання розв’язку нестаціонарних лінійних систем керування через фундаментальний розв’язок
Лінійна багатовимірна неперервна система керування описується рівнянням
. (5.1)
Використаємо відомі результати з теорії лінійних диференціальних рівнянь зі змінними коефіцієнтами. З цієї теорії нам відомо, що лінійно-незалежні розв’язки
|
|
|
( 
)
однорідного рівняння
(5.2)
утворюють фундаментальну матрицю
. (5.3)
Фундаментальну матрицю можна знайти як розв’язок матричної задачі Коші
. (5.4)
Для фундаментальної матриці існує обернена матриця 
в такому розумінні, що
= 
. (5.5)
Знайдемо розв’язок рівняння (5.1) за нульових початкових умов. Запропонуємо наступний алгоритм. Диференціюючи рівність (5.5), одержимо
.
Використовуючи (5.4), останнє співвідношення перепишемо так:
.
Звідси
або
. (5.6)
Співвідношення (5.6) помножимо на вектор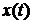 
, який задовольняє рівняння (5.1) за початкових умов 
. Тоді одержимо
.
Замість виразу 
підставимо його значення з рівняння (5.1). Тоді
або
.
Інтегруючи цю рівність в межах від 0 до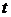 
, одержимо
.
Помножимо останню рівність на матрицю 
. Тоді остаточно маємо
. (5.7)
Зробивши позначення
(5.8)
рівність (5.7) запишемо у вигляді
. (5.9)
|
|
|
(5.10)
Поняття спряжених систем. Теорема про властивості розв’язків та фундаментальних матриць лінійних систем і спряжених систем
Означення 6.1 Дві системи, які описуються рівняннями
(6.1)
, (6.2)
де 
– матриця транспонована до матриці 
, називаються спряженими.
Теорема 6.1 Нехай 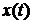і 
– деякі розв’язки рівнянь (6.1) і (6.2); 
і 
– фундаментальні матриці цих рівнянь, тобто розв’язок задачі (5.4), а – розв’язок задачі
. (6.3)
Тоді справджуються рівності
; (6.4)
. (6.5)
Доведення. Розглянемо вираз
Тут використано означення транспонованої матриці. Отже рівність (6.4) доведена.
Рівність (6.5) доведемо аналогічно. Дійсно, те що добуток 
сталий випливає з того, що
.
Оскільки при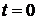 
цей добуток дорівнює 
(обидві матриці при 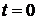одиничні), то рівність (6.5) справджуватиметься для всіх 
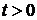за теоремою існування і єдиності розв’язку однорідної системи диференціальних рівнянь.
З рівності (6.5) випливає, що
.
Тому імпульсну перехідну матрицю (5.8) системи можна записати так:
|
|
|
.
З цієї причини спряжені системи грають важливу роль в теорії лінійних нестаціонарних систем.
Дата добавления: 2018-05-13; просмотров: 210; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!