Линейные преобразования случайных функций.
Пусть на вход линейной системы с оператором L воздействует случайная функция X (t), причем известны ее характеристики: математическое ожидание mx(t) и корреляционная функция Kx(t, t'). Реакция системы представляет собой случайную функцию Y(t) = L(X(t)).
Требуется найти характеристики случайной функции Y(t) на выходе системы: my(t) и Ky(t, t'). Короче: по характеристикам случайной функции на входе линейной системы найти характеристики случайной функции на выходе.
Покажем сначала, что можно ограничиться решением этой задачи только для однородного оператора L. Действительно, пусть оператор L неоднороден и выражается формулой:
L(X(t)) = L0(X(t))+ρ(t).
где L0—линейный однородный оператор, ρ(t)— определенная неслучайная функция. Тогда
my(t) = M[L0{X(t)}] + ρ(t).
т. е. функция ρ(t) просто прибавляется к математическому ожиданию случайной функции на выходе линейной системы. Что же касается корреляционной функции, то, как известно, она не меняется от прибавления к случайной функции неслучайного слагаемого.
Поэтому в дальнейшем изложении под «линейными операторами» будем разуметь только линейные однородные операторы.
Решим задачу об определении характеристик на выходе линейной системы сначала для некоторых частных видов линейных операторов.
Задача 32.11
Экзаменационный Билет №29
Теорема умножения вероятностей.
Событие А называется зависимым(независимым) от события В, если вероятность события А (не) зависит от того, произошло событие В или нет.
|
|
|
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А|В).
Условие независимости события А от события В можно записать в виде: Р(А|В) = Р(А), а условие зависимости в виде: Р(А|В) ≠ Р(А).
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
P(AB) = Р(А)*Р(В\А) = P(B)*P(A\B).
Интегральное преобразование случайных функций.
Дана случайная функция X (t) с математическим ожиданием mx (t) и корреляционной функцией Kx(t, t'). Случайная функция Y (t) связана с X (t) линейным однородным оператором интегрирования:
Y(t) = 
Требуется найти характеристики случайной функции Y (t): my(t) и Ky(t, t’).
Y(t)= = 
По теореме сложения математических ожиданий имеем:
my(t) = M[Y(t)] = 
= 
= 
Итак my(t) =
т. е. математическое ожидание интеграла от случайной функции равно интегралу от ее математического ожидания.
Найдем корреляционную функцию Кy(t, t'). Для этого перейдем к центрированным случайным функциям:
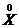(t) = X(t) – mx(t); 
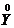(t) = Y(t) – my(t)
|
|
|
Нетрудно убедиться, что 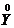(t) = 
По определению корреляционной функции,
Ky(t, t') = M[ 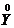(t) 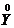(t’)]= 
Таким образом, для того чтобы найти корреляционную функцию интеграла от случайной функции, нужно дважды проинтегрировать корреляционную функцию исходной случайной функции: сначала по одному аргументу, затем — по другому.
Задача 3.16
Экзаменационный Билет №30
Дата добавления: 2018-05-13; просмотров: 330; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!