Примеры расчета частотных характеристик

⇐ ПредыдущаяСтр 2 из 2

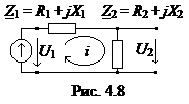
Пример 1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис. 4.8), рассчитать ее частотные характеристики:

Z_вх(jw), Z_вх(w), j_Z(w);

K(jw), K(w), j_K(w).

Решение. По определению Z_вх(jw) = 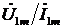. Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:

Z_вх(jw) = U_1m/I_1m = I_1m(Z₁+ Z₂); I_1m = (R₁+R₂) + j(X₁+X₂) = R + jX;

;

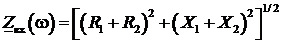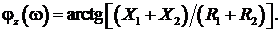
Используя определение K_u(jw) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:

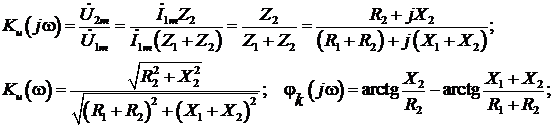
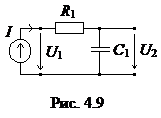Пример 2.Для интегрирующей RC-цепи, изображенной на рис. 4.9, рассчитать:

z_вх(jw), z(w), j_z(w);

K_u(jw), K(w), j_K(w).

От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис. 4.8.

Используя определение z_вх(jw) и законы Ома и Кирхгофа, получим его выражение

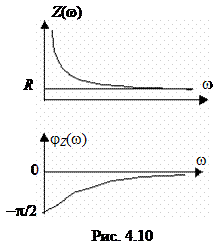Определим АЧХ и ФЧХ для z_вх(jw) и построим их графики (рис. 4.10), подсчитав значения при w = 0, w = ¥:

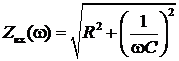; Z_вх(0) = ¥; Z_вх(¥) = R.

j_z(w) = – arctg 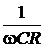; j_z(0) = –p/2; j_z(¥) = 0.

Используя определение K_u(jw), получим его выражение

K_u(jw)= = = = .

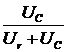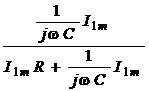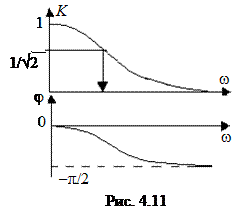
Определим АЧХ и ФЧХ для K_u(jw) и построим их графики (рис. 4.11), подсчитав значения при w = 0, w = ¥.

Учитывая, что

Z = = ,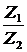

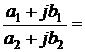
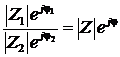где 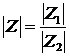, . Тогда

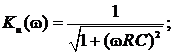K_u(0) = 1; K_u(¥) = 0.

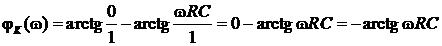Отсюда следует

φ_K(¥) = –π/2, φ_K(0) = 0.

Такая цепь пропускает сигналы низких частот (K_u(0) = 1) и подавляет сигналы высоких частот (K_u(¥) = 0), т.е. является фильтром низких частот (ФНЧ).

Граничная частота определяется из выражения 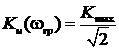. Рассчитаем ее для нашего примера:

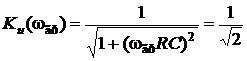; w_грRC =1 Þ .

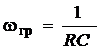Построим годограф передаточной функции (график АФЧХ К_u).

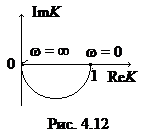При .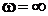

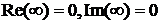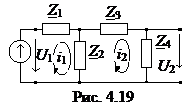
Учитывая, что реальная часть всегда положительна и уменьшается от 1 до 0, а мнимая часть всегда отрицательна, можно построить график годографа (рис. 4.12).

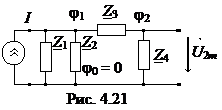
Пример 3.Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис. 4.19), рассчитать ее частотные характеристики:

Z_вх(jw), Z_вх(w), j_z(w), K(jw), K(w), j_K(w).

Решение. Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.

По определению, Z_вх(jw) = 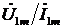. Входное сопротивление находим методом последовательных эквивалентных преобразований (рис. 4.20).

Z₁₂₃₄

Z₂₃₄

Z₁

U₁

U₂

U₁

Z₃₄

Z₂

Z₁

а б в
Рис. 4.20

найдем КЧХ коэффициента передачи по напряжению. По определению, K_u(jw) = U_2m/U_1m, а U_2m = Z₄İ₂ находим по закону Ома.

Отсюда видно, что для расчета КЧХ необходимо найти İ₂. Находим İ₂ методом контурных токов. Для этого определим число независимых контуров: N_k = b – у + 1 = 3 – 2 + 1 = 2, каждому из них присвоим свой контурный ток İ₁, İ₂ и составим уравнения по методу контурных токов.

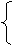Z₁₁İ₁+ Z₁₂İ₂ = E₁₁;Z₂₁İ₁+ Z₂₂İ₂ = E₂₂,

где Z₁₁ – собственное сопротивление первого контура, Z₁₁= Z₁+Z₂;

Z₁₂ и Z₂₁ – сопротивление смежных контуров, Z₁₂= Z₂₁ = –Z₂;

Z₂₂ – собственное сопротивление второго контура, Z₂₂= Z₂+Z₃+Z₄;

Ė₁₁– алгебраическая сумма источников ЭДС первого контура, Ė₁₁= U₁_m;

Ė₂₂ – алгебраическая сумма источников ЭДС второго контура, во втором контуре источников ЭДС нет, Ė₂₂= 0.

Найдем İ₂ – ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:

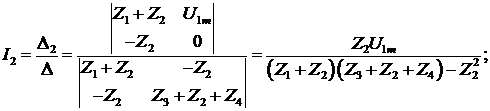
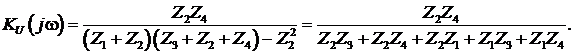
Найдем КЧХ другим способом, используя для расчета U₂_m метод узловых потенциалов. Для этого:

· преобразуем исходную схему к виду, показанному на рис. 4.21, заменив источник ЭДС на источник тока;

· потенциал узла 0 примем равным нулю, j₀= 0.

Тогда , _.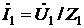

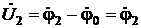Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее относительно j₂ по методу Крамера:

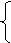Y₁₁j₁+ Y₁₂j₂= İ₁₁;Y₂₁j₁+ Y₂₂j₂= İ₂₂,

где Y₁₁ – собственная проводимость первого узла, Y₁₁= (1/Z₁)+(1/Z₂)+(1/Z₃);

Y₁₂и Y₁₂ – межузловая проводимость Y₁₂= Y₂₁= –1/Z₃;

Y₂₂ – собственная проводимость второго узла Y₂₂= (1/Z₃) + (1/Z₄);

j_1,j₂– потенциалы первого и второго узлов;

İ_11, İ₂₂ – токи источников токов, сходящихся в первом и втором узлах.

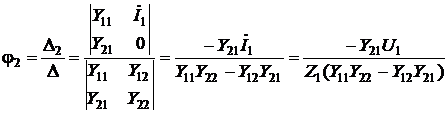
Отсюда следует, что

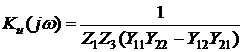
Для построения ФЧХ необходимо пользоваться следующими формулами:

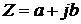, где a – реальная часть, а b – мнимая (рис. 5.16). Φ_Z =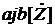

I 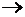a > 0, b > 0; φ = arctg ;

II a < 0, b > 0; φ = – arctg ;

III a < 0, b < 0; φ = + arctg ;

IV a > 0, b < 0; φ = – arctg .

4.3. Резонансные цепи. Колебательные контуры

Явление резкого возрастания амплитуды отклика при приближении частоты внешнего воздействия к определенному значению частоты называется резонансом. Такой резонанс имеет место в механике и называется амплитудным резонансом. Частота, на которой выполняется условие резонанса, называется резонансной частотой.

В электротехнике величины, характеризующие режим работы цепи на разных элементах, имеют амплитудный резонанс на разных, хотя и близких частотах. Поэтому в теории цепей под резонансом понимают фазовый резонанс. Под фазовым резонансом понимают условие, при котором цепь, содержащая реактивные элементы (L и C), имеет входное сопротивление резистивное, т.е. при резонансе ток и напряжение находятся в одной фазе, как и на любом резистивном элементе, а сдвиг по фазе равен нулю.

Электрические цепи, в которых имеет место явление резонанса, называются резонансными. Поскольку переходные характеристики резонансных цепей имеют колебательный характер, то резонансные цепи называют колебательными контурами.

Колебательные контуры используются для решения задач частотной избирательности. Под частотной избирательностью понимают способность цепи выделять сигналы узкого диапазона частот. К простейшим колебательным контурам относят последовательный и параллельный колебательный контур, также систему связанных контуров.

4.3.1. Последовательный колебательный контур

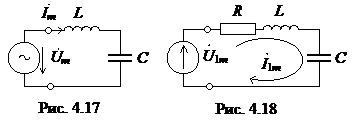
Последовательный колебательный контур состоит из последовательного соединения индуктивности L и емкости C (рис. 4.17).

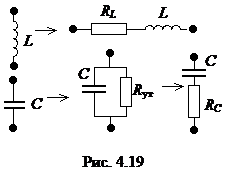
Для анализа процессов, протекающих в контуре, воспользуемся эквивалентной схемой замещения контура, в которой учтем резистивные сопротивления потерь реальных реактивных элементов (рис. 4.18). Схемы замещения реактивных элементов с учетом их резистивных сопротивлений приведены на рис. 4.19. Здесь R_L – резистивное сопротивление провода катушки индуктивности, R_ут– сопротивление утечки диэлектрика конденсатора, R_C – сопротивление утечки, пересчитанное в последовательную ветвь. Схема замещения последовательного контура приведена на рис. 4.18. В ней 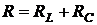– резистивное сопротивление контура, учитывает резистивные сопротивления реактивных элементов.

Определим частотную характеристику входного сопротивления последовательного колебательного контура:

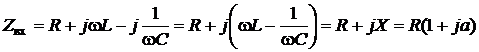где R – резистивная и 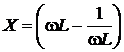– реактивная составляющая сопротивления последовательного колебательного контура;

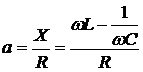
– обобщенная расстройка колебательного контура.

Характер входного сопротивления Z_вх(jω) зависит от частоты.

1) На низких частотах (НЧ) 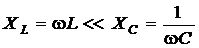; X < 0. Это означает, что сопротивление носит емкостной характер, его можно представлять эквивалентной схемой, приведенной на рис. 4.20, а.

2) На высоких частотах (ВЧ) 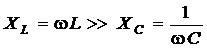, Х > 0, сопротивление последовательного контура носит индуктивный характер (рис. 5.20, б).

3) На некоторой частоте 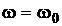, , 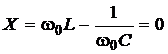Х = 0, сопротивление контура имеет резистивный характер, а его схема замещения состоит из резистора R.

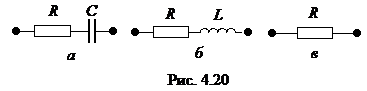Частота, на которой выполняется это условие, называется резонансной, она определятся как ω₀= (LC)^–1/2 .

Отметим свойства последовательного контура на резонансной частоте:

1) 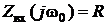сопротивление имеет резистивный характер и минимально по сравнению с сопротивлением на других частотах.

2) Начальные фазы напряжения и тока на контуре одинаковы φ_u= φ_i, сдвиг по фазе равен φ = φ_u – φ_i = 0.

3) Амплитуда тока в контуре максимальна и равна .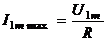

4) Сопротивления реактивных элементов L и C одинаковы и равны
– характеристическому сопротивлению контура, т.е.

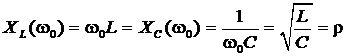5) Амплитуды напряжений на реактивных элементах контура одинаковы и в Q (добротность) раз больше (амплитуды напряжения на входе).

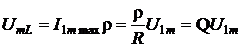, Q – добротность контура, .

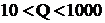Поэтому резонанс в последовательном контуре называется резонансом напряжений.

6) Амплитуды напряжений на реактивных элементах находятся в противофазах, а поэтому суммарное напряжение на реактивных элементах равно нулю: .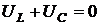

Резонансная характеристика последовательного колебательного контура

Это есть зависимость от частоты отношения комплексной амплитуде тока к комплексной амплилитуде тока при резонансной частоте, т.е.

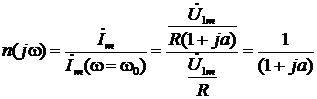Отсюда АЧХ: 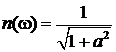(рис. 4.21); ФЧХ: .

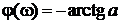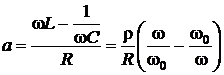– обобщенная расстройка,

w=w₀, a(w₀)=1, n=1.

На остальных частотах резонансная характеристика убывает:

w=0, a® – ¥, n=0; w®¥, a®¥, n=0.

Важным параметром колебательного контура является его полоса пропускания (S) – диапазон частот, в котором резонансная характеристика превышает уровень 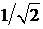, т.е. 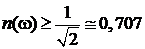, S = ω_в – ω_н, где ω_в, ω_н – верхняя и нижняя граничные частоты полосы пропускания (рис. 4.22).

0,707

Q₁

Q₂

Q₁

j(w)

w₀

n(w)

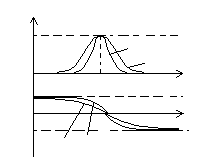
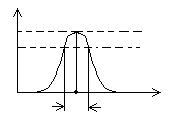
Рис. 4.21 Рис. 4.22

Параметры контура S, Q и ω₀ связаны соотношением . Отсюда следует, что чем больше добротность, тем меньше полоса пропускания, тем лучше избирательные свойства колебательного контура.

Зависимость добротности контура Q от сопротивления источника
сигнала (R_i) и сопротивления нагрузки (R_н)

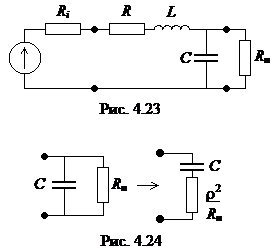Схема замещения последовательного колебательного контура с учетом добавочных элементов R_i, R_н представлена на рис. 4.23. Нагрузка подключена параллельно емкости. Параллельную RC цепь (с постоянными R и C) можно пересчитать на последовательную RC-цепь, ее параметры R_s C_s, однако, будут зависеть от частоты. Нетрудно показать, что если выполняется условие wRC>>1, тогда C_s@ C, и 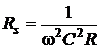. Вблизи резонансной частоты (w»w₀) 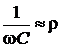. На рис. 4.24 показано эквивалентное преобразование параллельной RC цепи в последовательную, где .

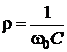Добротность контура с учетом добавочных элементов R_i, R_н называется эквивалентной и определяется из следующего выражения:

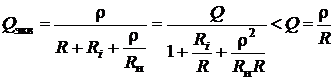Она меньше собственной добротности контура Q. Для того чтобы 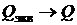, необходимо:

1) 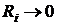. Это означает, что последовательный колебательный контур необходимо питать от источника ЭДС, т.е. источника с нулевым сопротивлением.

2) . В этом случае нагрузка не будет влиять на добротность контура.

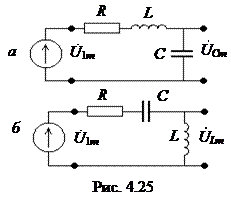Последовательный колебательный контур как четырехполюсник

На практике используются две схемы включения рис. 4.25. Для четырехполюсника основной частотной характеристикой является передаточная по напряжению.

1) .

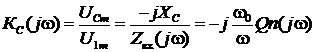2) .

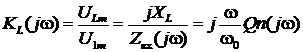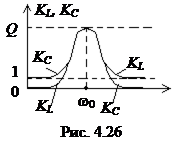Построим графики амплитудно-частотные характеристик этих зависимостей (рис. 4.26). Подробный анализ показывает, что при высоких добротностях резонансные частоты обеих схем совпадают и равны ω₀.

4.3.2. Параллельный колебательный контур

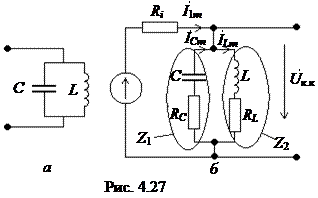Он состоит из параллельно соединенных двух реактивных элементов L и C. Его принципиальная схема приведена на рис. 4.27, а.

Схема замещения контура с учетом резистивных потерь реактивных элементов приведена на рис. 4.27, б.

Определим комплексное входное сопротивление параллельного колебательного контура

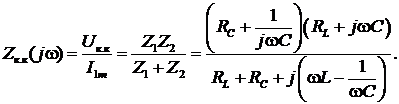
Обозначим 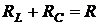– общие резистивные потери параллельного контура. При условии, что вблизи от резонанса 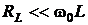; 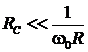, получим окончательное выражение для сопротивления параллельного колебательного контура.

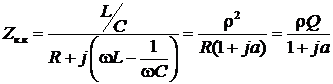Характер сопротивления параллельного колебательного контура зависит от частоты.

1) На НЧ 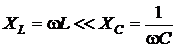– характер индуктивный. Схема замещения состоит из элементов R, L и приведена на рис. 4.28а,. Сопротивление контура Z_к.к(ω = 0) = R_L.

2) На ВЧ 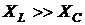сопротивление носит емкостной характер, (рис. 5.28б). Сопротивление контура Z_к.к(ω ®¥) = R_C.

3) На , когда 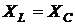, сопротивление контура имеет резистивный характер Z_к.к(ω₀) = ρQ (рис. 4.28в), где ω₀= (LC)^1/2 – резонансная частота.

а б в
Рис. 4.28

Отметим свойства параллельного контура на резонансной частоте.

1) Сопротивление контура имеет резистивный характер, и его модуль имеет максимальное значение по сравнению с сопротивлением на других частотах.

2) Ток и напряжение совпадают по фазе.

3) 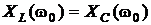– сопротивление реактивных элементов одинаково и равно .

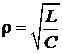4) Амплитуда тока через реактивные элементы в Q раз превышает ток во внешней цепи: 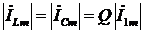, поэтому резонанс в параллельном контуре называется резонансом токов. Это вытекает из следующего:

; .

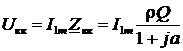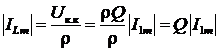5) Токи через реактивные элементы сдвинуты по фазе на 180°.

Построим графики АЧХ и ФЧХ входного сопротивления параллельного контура, которые определяются выражениями:

АЧХ: 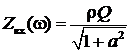; ФЧХ: .

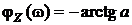Построенные графики приведены на рис. 4.29.

Резонансная характеристика параллельного колебательного контура

Она представляет собой зависимость от частоты отношения комплексной амплитуды напряжения на контуре к амплитуде напряжения на резонансной частоте : .

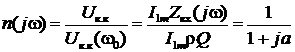Вид резонансной характеристики для последовательного и параллельного контуров одинаков, это их и объединяет. По характеру зависимости сопротивления от частоты они обладают противоположными свойствами (см. рис. 4.29).

Влияние сопротивлений источника сигнала и нагрузки на добротность параллельного колебательного контура

Схема замещения контура с учетом этих добавочных элементов приведена на рис. 4.30.

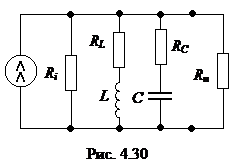Добротность контура с учетом паразитных элементов называется эквивалентной и определяется выражением

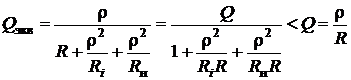Для того чтобы 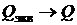, необходимо:

1) , т.е. контур питать от источника тока.

2) 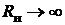, т.е. контур по выходу должен работать в режиме холостого хода.

4.3.3. Связанные колебательные контуры

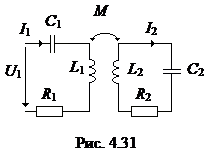Совокупность двух или более колебательных контуров, между которыми существует электрическая и магнитная связь, а энергия из одного контура может передаваться в другой, называется связанными колебательными контурами. Рассмотрим в качестве примера двухконтурную схему с трансформаторной связью (рис. 4.31).

Количественно степень связи между контурами оценивается с помощью коэффициента связи , .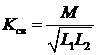

Составим и преобразуем уравнения для рассматриваемой схемы:

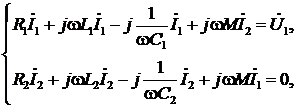
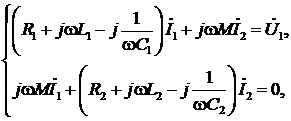
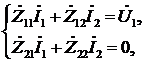
где Z₁₁, Z₂₂ – собственные комплексные сопротивления первого и второго контуров, Z₁₂=Z₂₁=Z_св– общее комплексное сопротивление первого и второго контуров, сопротивление связи.

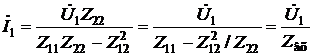Исследуем подробнее входное сопротивление

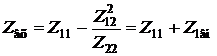где Z_1вн – комплексное сопротивление, вносимое из второго контура в первый,

Таким образом, активные и реактивные сопротивления определяются выражениями:

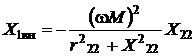Из системы уравнений найдем ток второго контура 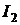с учетом того, что ,

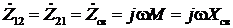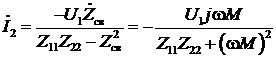Это выражение можно записать в виде

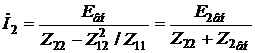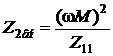
где – ЭДС, вносимая во второй контур, Z_2вн – вносимое сопротивление:

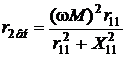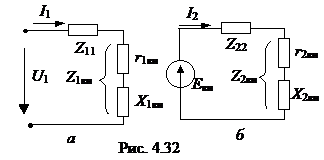
Схемы замещения первого и второго контура приведены на рис. 4.32.

Из приведенных выражений видно, что активные составляющие вносимых сопротивлений всегда положительны, а знаки реактивных составляющих вносимых сопротивлений противоположны знакам реактивных составляющих собственных сопротивлений вторичного и первичного контуров X₁₁ и X₂₂. Если, например, на какой-то частоте внешнего воздействия Z₁₁ имеет резистивно-емкостной характер, вносимое во вторичный контур Z_2вн будет иметь резистивно-индуктивный характер.

Резонанс в связанных колебательных контурах

При настройке связанных колебательных контуров добиваются наибольшего значения тока I₂ во вторичном контуре.

Настройку контуров можно вести как за счет изменения параметров реактивных элементов входящих в один или в разные контуры, так и за счет совместного изменения параметров реактивных элементов контуров и параметров элементов связи.

Есть несколько способов настройки связанных контуров.

1. Настройка на первый частный резонансосуществляется путем изменения параметров реактивных элементов, входящих только в первый контур (Z₂₂, Z₁₂ не изменяются), добиваясь равенства нулю суммы реактивной составляющей собственного сопротивления первичного контура и реактивной составляющей сопротивления, вносимого в первый контур:

X₁₁+ X_1вн=0

Этот способ соответствует настройке на резонансную частоту контура, эквивалентного первичному. Входное сопротивление такого контура относительно зажимов, к которому подключен источник энергии, имеет чисто резистивный характер и ток первичного контура максимален I₁_max. Ток второго контура при этом также максимален, поскольку он прямо пропорционален I₁_max:

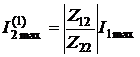
2. Настройку на второй частный резонансосуществляют путем изменения параметров реактивных элементов, входящих только во второй контур (Z₁₁, Z₁₂ не изменяются), добиваясь равенства нулю суммы реактивной составляющей собственного сопротивления второго контура и реактивной составляющей сопротивления, вносимого во второй контур:

X₂₂+ X_2вн=0

Ток второго контура при этом также достигает другого максимального значения .

3. Настройка на индивидуальный резонансосуществляется путем изменения параметров реактивных элементов, входящих в оба контура так, чтобы обеспечить равенство нулю мнимой составляющей каждого из контуров при разомкнутом другом контуре:

X₁₁ = X₂₂ = 0

При этом обеспечивается равенство нулю мнимых составляющих сопротивлений, вносимых в каждый из контуров: X_1вн = X_2вн = 0. Таким образом, при настройке на индивидуальный резонанс одновременно выполняются условия настройки на первый и второй частные резонансы.

Когда оба контура настроены 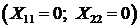, то 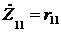, Z₂₂=r₂₂ и тогда модуль тока во втором контуре

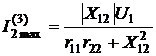Рассмотренные способы позволяют получить максимальное значение тока вторичного контура при некотором заданном значении сопротивления связи, однако не позволяют достигнуть наибольшего возможного (максимум максиморум) значения тока I₂.

4. Наибольший практический интерес представляет настройка на полный резонанс, которая проводится в два этапа: на первом этапе связанные контуры настраиваются на индивидуальный резонанс, а затем выбирают оптимальное сопротивление связи между ними.

Наибольшее возможное значение 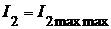будет иметь место при некотором значении сопротивления связи, которое называется оптимальным.

Приравняв нулю производную

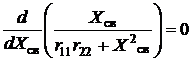найдем оптимальное сопротивление связи 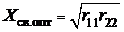, тогда .

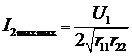Когда оба контура настроены по отдельности, а затем достигнута оптимальная связь, говорят, что связанные контуры настроены в полный резонанс.

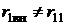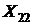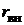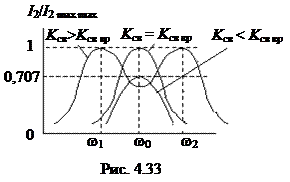
Если после настройки системы в полный резонанс усилить связь, то возрастут вносимые сопротивления. Теперь уже сопротивление , и во втором контуре не выделится наибольшая мощность. Однако можно вновь достичь выделения наибольшей мощности, если несколько расстроить вторичный контур. В этом случае возрастает реактивное сопротивление , что уменьшает вносимое активное сопротивление , и вновь можно добиться равенства 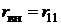, но уже при некоторых частотах, больших или меньших резонансной. Эти частоты называют частотами связи ( и 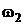) (рис. 4.33).

При полном резонансе оптимальный коэффициент связи

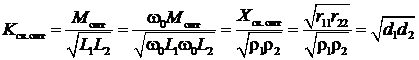где d₁ и d₂ – затухания контуров. Если связанные контуры имеют одинаковые параметры, то d₁ = d₂ и .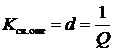

При одинаковых контурах оптимальный (критический) коэффициент связи численно равен затуханию любого из связанных контуров.

4.5. ОПЕРАТОРНЫЕ ФУНКЦИИ ЦЕПИ

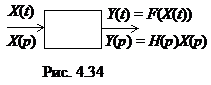Частотными функциями (характеристиками) цепи удобно пользоваться, когда входные сигналы являются гармоническими или представляются их суммой. В тех случаях, когда это не выполняется, удобнее пользоваться операторным представлением сигналов, а характеристики цепей представлять их операторными функциями.

Операторная функция цепи Н(р) есть отношение операторного представления отклика цепи к операторному представлению воздействия при нулевых начальных условиях

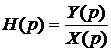, где .

Операторную функцию цепи можно получить из комплексной частотной функции (характеристики), заменив мнимую частоту jw комплексной частотой p: Н(р) = Н(jω)|_j_{ω =}_p. При этом частотную функцию нельзя подвергать каким либо преобразованиям, при которых мнимые единицы j перемножаются или сокращаются.

Названия операторных функций аналогичны названиям частотных характеристик, например

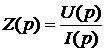– операторное сопротивление двухполюсника.

Для расчета операторной функций цепи необходимо от исходной схемы электрической цепи перейти к операторной схеме замещения, при этом сопротивление, емкость и индуктивность замещаются на операторные сопротивления, как показано на рис. 5.37.

Z_R = R

Z(p)_С =

Z(p)_L = pL

Z(p)

I(p)

U(p)

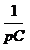
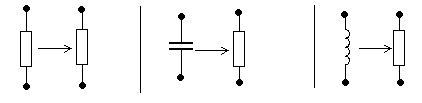
Рис. 4.35 Рис. 4.36

В общем случае операторная функция, как и частотная, цепей с сосредоточенными параметрами представляется отношением двух полиномов

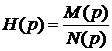Корни числителя называются нулями опер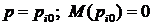аторной функции .

Корни знаменателя называются полюсами операторной функции. .

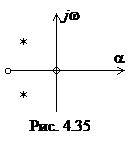
Нули и полюсы изображают точками на комплексной плоскости (рис. 5.21). Такой график называют картой нулей и полюсов. Свойства операторной функции оценивают по расположению нулей и полюсов на комплексной плоскости.

Контрольные вопросы

1. В чем заключается различие между откликом и воздействием?

2. Дать определение входным, выходным и передаточным параметрам четырехполюсника.

3. Как определяется частотный коэффициент передачи линейной цепи?

4. Дать понятия о годографе.

5. В чем заключается сущность амплитудного и фазового резонанса?

6. Каков фазовый сдвиг между входными напряжением и током на резонансной частоте на входе последовательного колебательного контура?

7. Как изменится добротность последовательного колебательного контура при подключении резистора параллельно с конденсатором контура?

8. Как изменится добротность последовательного колебательного контура при подключении резистора последовательно с элементами контура?

9. В каком колебательном контуре (узкополосной или широкополосной цепи) медленнее затухают собственные колебания?

10. Как называются резонансы в последовательном и параллельном колебательных контурах?

Дата добавления: 2018-05-12; просмотров: 10607; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!