Метод деления интервала пополам

 

Постановка задачи

 

Требуется найти безусловный минимум функции f(x) одной переменной т.е. такую точку , что .

 

Стратегия поиска

Метод относится к последовательным стратегиям и позволяет исключить из дальнейшего рассмотрения на каждой итерации в точности половину теку­щего интервала неопределенности. Задается начальный интервал не­определенности, а алгоритм уменьшения интервала, являясь, как и в общем слу­чае, "гарантирующим" (см. рис. 1.2), основан на анализе величин функции в трех точках, равномерно распределенных на текущем интервале (делящих его на че­тыре равные части). Условия окончания процесса поиска стандартные: поиск за­канчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.

 

Алгоритм

 

Шаг 1. Задать начальный интервал неопределенности L₀ = [a₀, b₀] и l > 0  требуемую точность.

Шаг 2. Положить к = 0.

Шаг 3. Вычислить среднюю точку , , .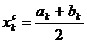

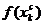Шаг 4. Вычислить точки: 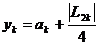,  и f(y_k), f(z_k). Заметим, что точки делят интервал [a_k, b_k] на четыре равные части.

Шаг 5. Сравнить значения  и :

а) если  < , исключить интервал , положив , . Средней точкой нового интервала становится точка y_k: . (рис. 1.4, а). Перейти к шагу 7;

б) если  ≥ , перейти к шагу 6.

Шаг 6. Сравнить  c :

а) если  < , исключить интервал , положив , . Средней точкой нового интервала становится точка z_k: . (рис. 1.4, б). Перейти к шагу 7;

б) если  ≥  исключить интервалы и , положив , . Средней точкой нового интервала останется : . (рис. 1.4, в).

 

Шаг 7. Вычислить  и проверить условие окончания:

а) если 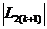 ≤ l, процесс поиска завершается и . В качестве приближенного решения можно взять середину последнего интервала: ,

б) если 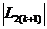 > l, то положить k = k + 1 и перейти к шагу 4.

 

 

Сходимость

 

Для метода деления интервала пополам характеристика относительного уменьшения начального интервала неопределенности находится по формуле , где N – количество вычислений функции.

 

Замечания 1.3:

1.Средняя точка последовательно получаемых интервалов всегда совпадает с одной из трех пробных точек, найденных на предыдущей итерации. Следова­тельно, на каждой итерации требуются два новых вычисления функции.

2.Если задана величина R(N), то требуемое для достижения желаемой точности количество вычислений функции находится как наименьшее целое, удовлетворяющее условию .

3.Текущие интервалы имеют четные номера L₀,L₂,L₄,..., где индекс ука­зывает на сделанное количество вычислений функции.

 

Метод дихотомии

 

Постановка задачи

 

Требуется найти безусловный минимум функции f(x) одной переменной т.е. такую точку , что .

 

Стратегия поиска

Метод относится к последовательным стратегиям. Задается начальный ин­тервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках (см. рис. 1.2). Для их нахождения текущий ин­тервал неопределенности делится пополам и в обе стороны от середины откла­дывается по 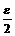, где  – малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего ин­тервала неопределенности оказывается меньше установленной величины.

 

Алгоритм

 

Шаг 1. Задать начальный интервал неопределенности L₀ = [a₀, b₀],
 > 0 – малое положительное числои l > 0 – точность.

Шаг 2. Положить k = 0.

Шаг 3. Вычислить , f(y_k), ,  f(z_k).

Шаг 4.Сравнить f(y_k) и  f(z_k).

а) если f(y_k) ≤  f(z_k), положить a_k+1 = a_k, b_k+1 = z_k (рис. 1.5, а) и перейти к шагу 5.

б) если f(y_k) >  f(z_k), положить a_k+1 = y_k, b_k+1 = b_k (рис. 1.5, б).

Шаг 5.Вычислить  и проверить условие окончания:

а) если 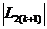 ≤ l, процесс поиска завершается и . В качестве приближенного решения можно взять середину последнего интервала: ,

б) если 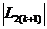 > l, то положить k = k + 1 и перейти к шагу 3.

 

Сходимость

 

Для метода дихотомии характеристика относительного уменьшения на­чального интервала неопределенности находится по формуле ,
где N – количество вычислений функции.

 

Замечания 1.4:

1. Текущие интервалы имеют четные номера L₀,L₂,L₄,..., где индекс ука­зывает на сделанное количество вычислений функции, как и в ме­тоде деления интервала пополам.

2. Эффективность методов дихотомии и деления интервала пополам при малых можно считать одинаковой.

 

Метод золотого сечения

 

Постановка задачи

 

Требуется найти безусловный минимум функции f(x) одной переменной т.е. такую точку , что .

Для построения конкретного метода одномерной минимизации, работаю­щего по принципу последовательного сокращения интервала неопределенности, следует задать правило выбора на каждом шаге двух внутренних точек. Желательно, чтобы одна из них всегда использовалась в качестве внутренней и для следующего интервала. Тогда число вычислений функции сократится вдвое и одна итерация потребует расчета только одного нового значения функции. В ме­тоде золотого сечения в качестве двух внутренних точек выбираются точки золо­того сечения.

 

Определение:Точка производит "золотое сечение" отрезка, если отноше­ние длины всего отрезка к большей части равно отношению большей части к меньшей.

На отрезке [a₀, b₀]имеются две симметричные относительно его концов точки у₀ и z₀:

Кроме того, точка у₀ производит золотое сечение отрезка [a₀, z₀], a точка z₀ – отрезка [y₀,b₀]:

 

 

Стратегия поиска

Метод относится к последовательным стратегиям. Задается начальный ин­тервал неопределенности и требуемая точность. Алгоритм уменьшения интер­вала опирается на анализ значений функции в двух точках (см. рис. 1.2). В каче­стве точек вычисления функции выбираются точки золотого сечения. Тогда с учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала не­определенности оказывается меньше установленной величины.

 

Алгоритм

 

Шаг 1. Задать начальный интервал неопределенности L₀ = [a₀, b₀]
 и l > 0 – точность.

Шаг 2. Положить k = 0.

Шаг 3. Вычислить , .

Шаг 4.Вычислить f(y_k) и  f(z_k).

Шаг 5.Сравнить f(y_k) и  f(z_k).

а) если f(y_k) ≤  f(z_k), положить a_k+1 = a_k, b_k+1 = z_k и y_k+1 = a_k+1+b_k+1-z_k,
z_k+1 = y_k (рис. 1.6, а) и перейти к шагу 6.

б) если f(y_k) >  f(z_k), положить a_k+1 = y_k, b_k+1 = b_k и y_k+1 = z_k,
z_k+1 = a_k+1+b_k+1- z_k (рис. 1.6, б).

 

Шаг 6.Вычислить  и проверить условие окончания:

 

а) если  ≤ l, процесс поиска завершается и . В качестве приближенного решения можно взять середину последнего интервала: ,

 

б) если  > l, то положить k = k + 1 и перейти к шагу 4.

 

Сходимость

 

Для метода золотого сечения характеристика относительного уменьшения начального интервала неопределенности находится по формуле 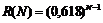, где N - количество вычислений функции.

 

Замечания 1.5.

 

1.Текущие интервалы неопределенности имеют следующий вид: L₀,L₂,L₃, L₄,...,. Они отражают тот факт, что на первой итерации производится два вычисления функции, а на последующих – по одному.

 

2.Сокращение длины интервала неопределенности постоянно:

 

3.Если задана величина R(N), то требуемое для достижения желаемой точности количество вычислений функции находится как наименьшее целое число, удовлетворяющее условию

---

Дата добавления: 2018-04-15; просмотров: 494; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!