Расчет составных балок на постоянную нагрузку
ГЛАВА 2. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК НА СИЛОВУЮ НАГРУЗКУ
Основные понятия
Балками называются конструкции, назначение которых – перекры-вать один либо несколько пролетов. При действии вертикальной нагрузки балки работают на изгиб. Общепринято, что изгибаемые элементы назы-
вают балочными элементами.
Рассмотрим виды статически определимых балок, представляющих собой один диск, присоединенный к «земле» тремя опорными связями.
| а) | а) | M1 | F | ||||
| l | l | ||||||
| б) | б) | F | |||||
| l | M 2 | ||||||
| l | |||||||
| в) | в) | F1 M 3 | F | M 5 F2 | |||
| a | l | b | a | M 4 | |||
| l | b |
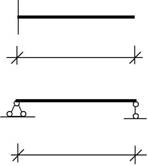


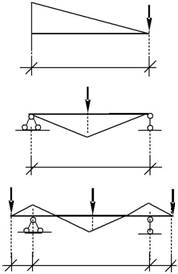
Рис. 2.1 Схемы балок:
а)жестко защемленная консоль; б)однопролетная балка; в)опорно-консольная балка.
Рис. 2.2. Эпюры моментов:
а)для жестко защемленной консоли б)для однопролетной балки; в)для опорно-консольной балки.
Исследуем эпюры моментов, построенные в каждой балке от дейст-вия сосредоточенных сил на рис. 2.2.
1. В схеме а) наибольший(расчетный)момент M1 =F⋅l от силы F воз-никает в сечении, примыкающем к жесткой заделке.
2. В однопролетной балке (схема б) расчетный момент M2 возникает
в точке приложения сосредоточенной силы F. Если сила приложена посе-
редине пролета, этот момент будет равен F⋅l/4.
3. В схеме в) нагрузка на консолях создает моменты сечениях на опо-рах (M3, M5), уменьшая при этом пролетный момент (M4< M2).
4. Назначим числовые значения размерам и силам: a = 1 м; b = 1,5 м;
l = 6м, F = 12кН; F1= 6кН; F2 = 2кН.В схемах б) и в) силу F приложимв середине пролета. Сравним значения расчетных моментов в балках:
M1 =72кНм; M2=18кНм; M3 = 6кНм; M4=13,5кНм; M5 =3кНм.
Таким образом, расчетные моменты в схеме в) оказались наименьшими.
24
2.2. Расчёт многопролётных составных балок
Для перекрытия нескольких пролётов используются многопролёт-ные балки.Если балка при этом представляет собой один диск (рис. 2.3, а),она является статически неопределимой, так как имеет более 3-х опорных связей. Такая балка называется неразрезной.
а)
б)
в)
г)
Эп. M
д) 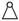
Эп. M
е)
Эп. M
а)
| Число лишних | связей | неразрезной | |
| балки равно С0 –3 . Именно столько | |||
| шарниров необходимо врезать в балку, | |||
| чтобы она стала статически определи- | |||
| мой. Разрез шарнирами делается либо | |||
| на опорах (рис. 2.3, б), тогда балка на- | |||
| зывается разрезной, либо | в пролётах | ||
| (рис. 2.3, в), тогда балка называется | |||
| составной,так как состоит из не- | |||
| q | скольких дисков. | ||
| Таким образом, в статически оп- | |||
| ределимой составной балке соотноше- | |||
| M0max | ние шарниров и опорных связей долж- | ||
| но быть следующим: | |||
| Ш= С0 – 3 | |||
| На рис. 2.3, г для каждой схемы балок | |||
| M0max | показаны эпюры моментов от дейст- | ||
| вия равномерно распределённой на- | |||
| грузки. Распределение моментов на | |||
| рис. 2.3, г, е считается более опти- | |||
| мальным, так как максимальные про- | |||
| 0 | летные моменты здесь меньше, за счет | ||
| M max Mmax | возникновения | моментов | в опорных |
| сечениях. | |||
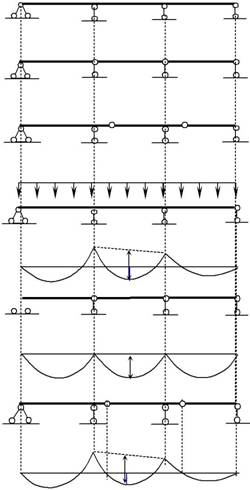
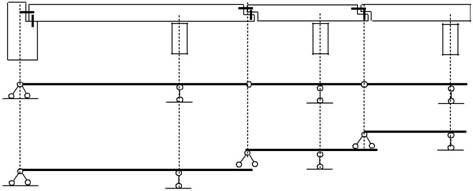
| Рис. 2.3 | На рис. 2.4, а показано, как вы- | ||
| глядит составная балка «в теле». | |||
| б) А | B | C | D |
| C | D |
B
в) А
Рис. 2.4
25
Для расчета составных балок удобно использовать рабочую (по-этажную) схему.Рассмотрим построение поэтажной схемы на примеребалки, изображённой на рис. 2.4, б.
Диск A-B имеет три связи с землёй. Такой диск считается главным. Шарнир В имеет две внутренних связи и может быть представлен как шар-нирно-неподвижная опора, с помощью которой диск B-C опирается на диск A-B. Таким же образом диск C-D опирается на диск B-C. Диски B-C и C-D называют второстепенными.Второстепенные диски могут быть от-брошены без нарушения неизменяемости системы . Если поэтажная схема составлена верно, то каждая простая балка в этой схеме имеет три опор-
ных связи (рис. 2.4, в).
Покажем другие схемы составных балок.
Случай расположения двух шарниров в одном пролёте (рис. 2.5).В
этом случае диск B-C поднимается над левым и правым диском и является второстепенным. Диски A-B и C-D являются главными. Горизонтальная связь с опоры С переносится на опору правого главного диска C-D.
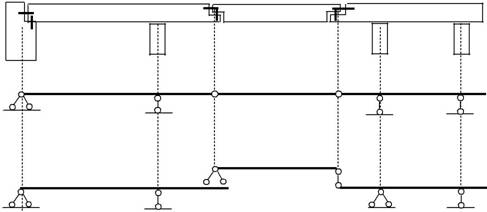
А B C D
| B | C | D | |
| А | |||
| Рис. 2.5 |
Случай расположения шарниров через пролет (рис. 2.6).ДискиA-B
и C-D в этом случае становятся второстепенными, а диск B-С главным.
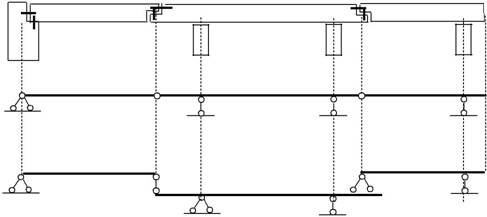
А B C D
А B C D
Рис. 2.6
26
Расчет составных балок на постоянную нагрузку
Если на балку действует вертикальная нагрузка, она испытывает только деформации изгиба. Следовательно, в сечениях балки возникают только два внутренних усилия − изгибающий момент М и поперечная сила Q.Таким образом,расчёт на постоянную нагрузку предполагает построе-ние эпюр M и Q и определение по этим эпюрам экстремальных (расчет-ных) значений.
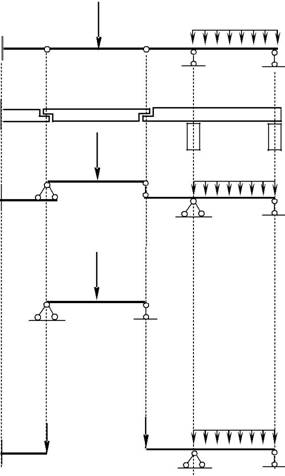
Если поэтажная схема балки построена , расчет производится сверху вниз. На рис. 2.7приведён пример передачи нагрузки с второстепенногодиска B-C на главные диски A-B и C-D.
Второстепенный диск, расположенный выше остальных, работает только на местную нагрузку (рис. 2.7, г). При расчёте нижележащих дис-ков необходимо учитывать давление, передаваемое с верхних дисков. Это давление моделируется сосредоточенной силой, численно равной реакции связи, соединяющей эти диски, но противоположно направленной (рис. 2.7, д). Таким образом, каждая простая балка может быть рассчитана неза-висимо.
| F | q | ||||
| а) | AB | C | D | ||
б)
F
q
в)
F
| г) | B | C | |
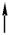 VB
VB 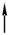 VC
VC
| VB | VC | q | ||||
| д) | A | B | C | D | ||
Рис. 2.7
27
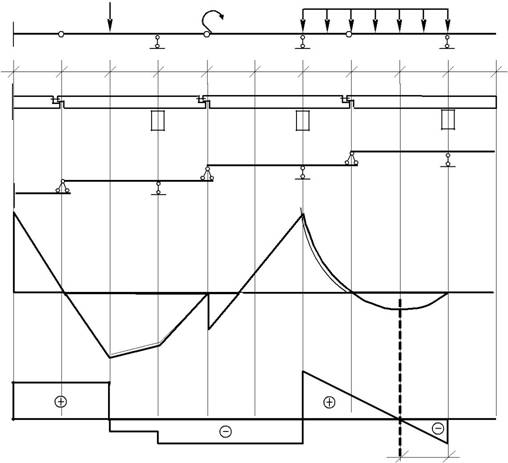
Пример 2.1. Дана3-х пролетная составная балка,загруженная силовой на-грузкой (рис. 2.8). Требуется построить эпюры M и Q .
| F=16кН | M=24кНм | q=2кН/м | |
| 4 м4 м | 4 м4 м4 м4 м 4 м | 4 м4 м4 м | |
| G | L | R Поэтажная | |||||
| B | C | D | E | схема балки | |||
| A | |||||||
| 50 | 48 | ||||||
| 12 | M | ||||||
| (кНм) | |||||||
| 16 | |||||||
| 12,5 | 50 | 36 | 24 | 16 | Q | ||
| 12,5 | |||||||
| 8 | (кН) | ||||||
| 3,5 | 9 | 9 | 4 м | 8 | |||
Рис. 2.8
Решение
1. Показываем поэтажную схему балки.
2. Каждый диск рассчитываем отдельно, как простую балку (алго-ритм построения эпюр в простых балках по характерным точкам подробно рассмотрен в приложении В). Расчет начинаем с верхнего диска G-L-R.
| q=2кН/м | Диск G-L-R (рис. 2.9) | |||||||
| G | O | L | R | ∑M L =0; −VG ⋅8 + 2 ⋅8 ⋅4 =0; VG=8 кН; | ||||
| VG | 4 м | VL | ∑MG =0; | VL ⋅8−2⋅8⋅4=0; VL=8кН. | ||||
| 4 м | 4 м | УчастокL-R. ML-R=MR-L=0 ; | QL-R=0. | |||||
| M (кНм) | ||||||||
| 16 | Участок G-L. | MG-L=ML-G=0 . | ||||||
| 8 | Q (кН) | M 0=8⋅4− | 2 ⋅42 | =16 кНм | ||||
| 8 | 2 | |||||||
| QL-G=8кН; QG-L= – 8кН. | ||||||||
| Рис. 2.9 | ||||||||
| 28 | ||||||||


| M=24кНм | q=2кН/м VG=8кН | |||||
| D | E | G | ||||
| VD | 8 м | VE | 4 м | |||
| 48 | ||||||
| M | ||||||
| 24 | (кНм) | |||||
| 16 | ||||||
| 8 Q (кН) | ||||||
| 9 | ||||||
| Рис. 2.10 | ||||||
| F=16кН | VD=9кН | |||||
| B | P | C | D | |||
| VB 4м | 4 м | 4 м | ||||
| VC | M | |||||
| (кНм) | ||||||
| 12,5 | 50 | 36 | ||||
| Q (кН) | ||||||
| 3,5 | 9 | |||||
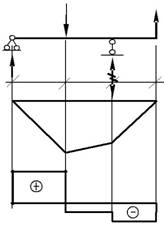 Рис. 2.11
Рис. 2.11
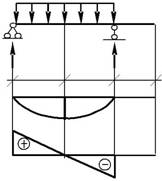
Диск D-E-G (рис. 2.10).
∑ M E =0;−VD ⋅8−24−2⋅4⋅2−8⋅4=0;
VD = –9кН
∑ M D =0; VE ⋅8−24−2⋅4⋅10−8⋅12=0; VЕ
= 25 кН
| Проверка: | ∑Y =0; | −VD +VE −q⋅4−VE = | ||
| =–9+25–2⋅4-8=0 (выполняется). | ||||
| Участок E-G. M GE | = 0 ; | |||
| M E−G = −8⋅ | 4 − | 2 ⋅42 | = −48 кНм; | |
| 2 | ||||
| QG-E=8кН; | QE−G =8+2⋅4=16кН. | |||
Участок D-E. MD-Е = M=24кНм;
ME-D = ME-G = – 48кНм; QD-E = – 9кН.Диск В-C-D (рис. 2.11).
∑ M С =0;−VB ⋅8+9⋅4+16⋅4=0;
VB = 12,5кН;
∑ M B =0; VC ⋅8−16⋅4+9⋅12=0;
VC = – 5,5кН.
Проверка: ∑Y = 0; VB −VC − F +VD =
=12,5–5,5 –16+9 =0 (выполняется).
Участок C-D: MD-C = 0;
MC-D = 9⋅4=36кНм; QC-D = – 9кН.
Участок B-P: MB-P = 0;
MP-B = VB⋅4=12,5⋅4= 50кНм; QB-P = VB = 12, 5кН.
| A | B VB=12,5кН | |
| 4 м | M | |
| 50 | (кНм) | |
| 12,5 | Q | |
| (кН ) |
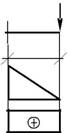
Диск A-B (рис. 2.12).
MB-A = 0; MA-B = – 50кНм; QA-B = 12,5кН.
Рис. 2.12
3. Объединяем построенные эпюры в один график, и строим эпюры для составной балкой (рис. 2.8.)
29
Задания для закрепления темы
(для решения рекомендуется обратиться к материалу, рассмотренному в приложениях Б и В)
1. Из какого условия подбираются уравнения статики для определе-ния опорной реакции в статически определимых системах?
2. Дана система взаимно уравновешенных векторов (рис. 2.13). Век-тора F1 и F2 известны. Подберите уравнение статики для определения век-
тора V3.
F1 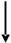 V1 F2
V1 F2 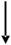
 V2
V2

V3
Рис. 2.13

3. Покажите ось, проекция вектора V1 на которую будет нулевой.
4. Для балки, изображенной на рис. 2.14, запишите по пунктам алго-ритм определения момента в точке O. Определите Mo через внешний мо-мент M и расстояние a. Объясните правило знаков.
| O | М | |||
| а | 2a | a | a | Рис. 2.14 |
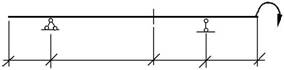
5. Для этой же балки запишите по пунктам алгоритм определения поперечной силы в точке O через M и a. Объясните правило знаков.
6. Покажите деформированную схему балки на рис. 2.14.
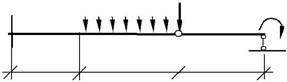
7. 8. Для балки на рис. 2.15 постройте эпюры M и Q . Определите ре-акции, которые для этого необходимы.
| q=1кН/м | F=10кН М=12кНм | ||||||||
| Рис. 2.15 | |||||||||
| 2 м | 6 м | ||||||||
| 3 м | |||||||||
|
|
|
|
| ||||||
Дата добавления: 2018-04-04; просмотров: 487; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
