Метод интегрируемых комбинаций
Метод заключается в том, что посредством арифметических операций из уравнений системы (22.73) получают легко интегрируемые уравнения относительно новой неизвестной функции.
Пример 1. Решить систему:
1) 
2) 
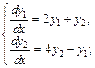3) 
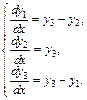
Решение. 1) Используем метод исключения. Дифференцируем первое уравнение системы по x:
Подставив в полученное уравнение из второго уравнения системы выражение вместо 
имеем:
или
(22.74)
Последнее уравнение – линейное неоднородное дифференциальное уравнение 2-гопорядка со специальной правой частью. Его соответствующее однородное уравнение:
Характеристическое уравнение последнего:
корни которого 
Тогда общее решение однородного уравнения:
Ищем частное решение полученного неоднородного уравнения (22.74) в виде
где A, B – неопределенные коэффициенты.
Вычисляем производные:
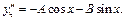
Подставляем их в уравнение (22.74), группируем относительно sin x и cos x, приравниваем коэффициенты.
Получаем систему 
из которой находим 
Общее решение дифференциального уравнения 2-гопорядка:
(22.75)
Возвращаемся к первому уравнению заданной системы, из которого выражаем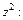 
Подставляя в это уравнение продифференцированное общее решение (22.75), получим:
(22.76)
Функции (22.75) и (22.76) составляют общее решение заданной системы.
2) Применим метод исключения. Выразим из первого уравнения системы 
Отсюда, дифференцируя по x, получим:
Подставим правую часть полученного равенства вместо 
во второе уравнение системы:
|
|
|
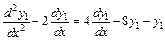или
Получили однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Его характеристическое уравнение: 
решая которое, находим: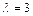 
– корень кратности 2.
Тогда
Продифференцируем функцию 
Возвращаясь к первому уравнению системы, имеем:
Упрощаем: 
Таким образом, получаем общее решение заданной системы:
3) Используем метод исключения. Дифференцируем первое уравнение системы:
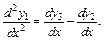
Подставив в него выражения для 
и из 2-го и 3-го уравнений системы, получим линейное однородное дифференциальное уравнение 2-го порядка: 
Его характеристическое уравнение имеет вид: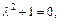 
корни которого 
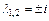– простые комплексно-сопряженные. Тогда общим решением однородного дифференциального уравнения будет:
Из третьего уравнения системы получаем:
Подставим в него найденное выражение для 
получим линейное неоднородное дифференциальное уравнение 1-го порядка:
(22.77)
Решим его методом Эйлера. Характеристическое уравнение соответствующего однородного 
корень которого 
Тогда общее решение соответствующего однородного:
Частное решение неоднородного дифференциального уравнения ищем в виде
где A, B – неопределенные коэффициенты.
|
|
|
Вычисляем 
и подставляем в неоднородное уравнение (22.77).
Для определения A и B приходим к системе
из которой находим 
Тогда получаем:
Из первого уравнения заданной системы выразим
Подставим в это равенство найденные 
и 
получим:
Таким образом, получено решение заданной системы дифференциальных уравнений:
Пример 2. Методом интегрируемых комбинаций решить систему
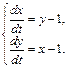
Решение. Воспользуемся методом интегрируемых комбинаций. Сложив оба уравнения системы, получим:
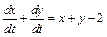или
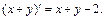
Обозначим 
где 
получим: 
– уравнение с разделяющимися переменными. Запишем его в виде
или
Отсюда находим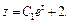 
Возвращаемся к старым переменным:
Выразим теперь y через x:
Продифференцируем это равенство и подставим вместо 
во 2-е уравнение системы:
После подстановки:
или 
– это линейное уравнение 1-гопорядка. Решим его методом Бернулли.
Пусть 
тогда 
Отсюда 
тогда
Это и есть общее решение исходной системы.
Дата добавления: 2015-12-17; просмотров: 50; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!