Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: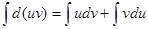 
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
или 
;
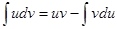Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Полученная формула называется формулой интегрирования по частям. По частям берутся интегралы вида:
1) 
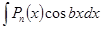
В этих интегралах в качестве u всегда берется 
Пример.
2) 
3) 
Здесь за u всегда принимают обратную тригонометрическую функцию.
4) 
За u принимают lnx.
Пример:
По частям берутся также интегралы вида:
и 
Двукратным применением формулы интегрирования по частям эти интегралы приводятся сами к себе (т.н. интегралы возврата). Получается алгебраическое уравнение относительно искомого интеграла.
Пример: 
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Дата добавления: 2015-12-16; просмотров: 18; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!