Производные и дифференциалы высших порядков
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ. ПРАВИЛА ЛОПИТАЛЯ
План
1. Производные и дифференциалы высших порядков.
- Теоремы Ферма, Ролля и Лагранжа. Теорема Коши.
- Правила Лопиталя.
Производные и дифференциалы высших порядков
Опр. Пусть функция 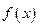 , определенная на интервале
, определенная на интервале 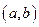 , в каждой точке
, в каждой точке 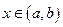 имеет производную
имеет производную 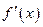 и пусть
и пусть 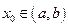 , Производная функции
, Производная функции 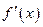 в точке
в точке 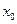 называется второй производной функции
называется второй производной функции 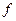 и обозначается
и обозначается  или
или  .
.
Таким образом,
 или
или  . (1)
. (1)
Аналогично определяется производная  любого порядка
любого порядка 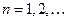 : если существует производная
: если существует производная  порядка
порядка 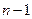 , то
, то  .
.
При этом под производной нулевого порядка подразумевается сама функция  .
.
Учитывая общее определение производной, представим производную 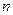 -го порядка в виде предела:
-го порядка в виде предела:
 ,
, 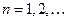 . (2)
. (2)
Если функция 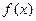 имеет в точке
имеет в точке 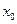 производную порядка
производную порядка 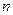 , т.е. что существует
, т.е. что существует  , то в силу определения производной существуют все производные порядка
, то в силу определения производной существуют все производные порядка  для функции
для функции 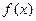 и сама эта функция определена в некоторой окрестности точки
и сама эта функция определена в некоторой окрестности точки 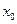 .
.
Опр. Функция 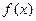 называется
называется 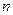 раз непрерывно дифференцируемой на некотором промежутке, если на этом промежутке существует производная
раз непрерывно дифференцируемой на некотором промежутке, если на этом промежутке существует производная 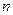 -го порядка
-го порядка  функции
функции 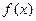 и эта производная непрерывна.
и эта производная непрерывна.
В качестве примера найдем производные функции  . Используя таблицу производных и определение для производной
. Используя таблицу производных и определение для производной 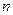 -го порядка, получаем
-го порядка, получаем
 ,
,  ,
,  ,
,  .
.
Другой пример связан с функцией  . Ее первая производная равна
. Ее первая производная равна  , а последующие имеют вид
, а последующие имеют вид
|
|
|
 ,
,  ,
,  ,
,
и так далее в том же порядке.
Учитывая формулы приведения:  , получаем:
, получаем:
 ,
,  и т.д.
и т.д.
Тогда для любого 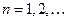 справедливо равенство
справедливо равенство  .
.
Дата добавления: 2016-01-06; просмотров: 15; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
