Интегральное преобразование Фурье.

Элементы теории сигналов и систем.

Классификация сигналов.

Сигналы классифицируются по следующим признакам :

1)

одномерные;

многомерные;(количество переменных больше 2х)

2)

Основанные на возможности или не возможности точного предсказания значения сигнала в любой точке пространственных координат.

V

V

В 1-ом случае сигнал детерминированный, а во 2-м – случайный сигнал описывается случайной функцией .Случайно функцию времени называют случайным процессом.

 

 

а)детерминированная функция,                                   б)случайная

       (периодичная)

Дискретизация сигнала заключается в замене непрерывных значений дискретными значениями и может осуществляться во времени, по уровню и во времени и уровню.

 

 

 

 

Преобразование Фурье непрерывных сигналов.

Разложение периодических сигналов в ряд Фурье.

Сигналы (t) называется периодичным, если x(t) = X(t+nT),

где

n = 1,2…;

T-период сигнала;

Примером периодичности сигнала является гармонические колебания, которые описываются следующим образом:

x(t) = A*cos(ωt- φ);

A – амплитуда сигнала;

ω – круговая частота

φ- начальная фаза сигнала

t – период

ω = 2πf; f = ; T = ;

Сложение гармоник сигналов может быть представлено кратными частотами ω, 2 ω, образующих сигнал вида:

x(t) =  + +…;

Тогда, суммарный сигнал будет периодический и будет определяться следующим уравнением:

X(t) =                                                                                         (1)

ω₁ – круговая частота 1-ой гармоники

В теории сигналов доказано, что периодический сигнал X(t) сложной формы, может быть разложен на элементарные гармонические колебания с амплитудой А_к с частотой kω₁t и сдвигом(начальным) по фазе φ_k.

Разложим периодический сигнал:

A_k*cos(kω₁t – φ_k)=A_k*cos(kω₁t)*cos φ_k + A_k *sin(kω₁t)*sin φ_k;

Подставим

A_k*cos φ_k = a_k;

A_k sin φ_k = b_k;

Тогда, выражение (1) записанное с учётом нулевой гармоники, примет вид:

X(t) =  + ,                                                                              (2)

где - нулевая гармоника;

Выражение (2) это разложение периодического сигнала в ряд Фурье.

Коэффициенты ряда Фурье определяются следующим образом:

a₀ = * ;

a_k = * ;

b_k = * ;

A_k =

Если x(t) – чётная функция на интервале [-T/2;T2], тогда

-> чётная функция, тогда

 -> не чётная функция.

Тогда в этом случае коэффициент b_k ряда Фурье равен 0.

Если x(t) – не чётная функция, то все наоборот, и а_k = 0;

Совокупность А_к и φ_k разложенные периодические функции(1) представляют амплитудные и фазовые периоды сигналов функции вида:

cosω₁t, sinω₁t, cos2ω₁t, sin2ω₁t, …, coskω₁t, sinkω₁t

Сумма функции, которая используется в разложении (2) обладает свойством заключающемся в том, что интеграл произведений любых 2-х функций на периоде T = 0 :

;

;

;

;

p – действительное число

l – натуральное число.

Представление в полной записи называется ортогональностью, а разложение (2) X(t) по ортогональному базису функции выражения (1).

 

Интегральное преобразование Фурье.

На практике часто используется непериодические сигналы, по этому обобщим ряд Фурье на случай непериодического сигнала и рассмотрим сигнал X_p(t), который представляет собой периодического последовательность импульсов X(t), следующих с периодом T.

X_p(t) = .

Функция X(t) описывает один импульс, коэффициенты ряда Фурье на интервале [-T/2;T/2] равны:

Сk =  *                                                                                        (3)

Учитывая, что сигнал на данном интервале может быть представлен одним импульсомX(t), тогда за пределами указанного интервала X(t) = 0 и тогда уравнение (3) может быть записано ввиде:

Сk = *                                                                                            (4)

Из уравнения (4) следует при T=const, коэффициенты C_k зависят только от интервала и тогда:

X(k,w₁)=                                                                                            (5)

Комплексная функция частоты X(k,ω₁)– спектральная характеристика единичного импульса.

Из уравнения (4) и (5) можно записать следующее:

C_k= ;

Пределы интегрирования в уравнении (5) являются бесконечными, что следует понимать как разложение в ряд одноименного импульса на интервале [ -∞;+∞ ]и тогда сигнал X(t) можно записать следующим образом, считая, что Tà∞ :

X(t) = ;

Так как T = , то

X(t) =                                                                       (6)

Так как при Tà∞ , частота первой гармоники ω₁ = она становится бесконечно малой величиной

Приращение частоты ω₁при переходе к соседней гармонике соответствует дифференциалу ω. Под знаком ∑ в уравнение (6) частотные гармоники принимают дискретные значения, то, как Tà∞, то частоты гармоник становятся бесконечно близкими.

Введём обозначение W = k*ω_1.

В этом случае в выражении (6) операция суммирования переходит в операцию интегрирования и тогда (5) и (6) имею следующий вид:

X(ω) =                                                                                                        (7)

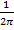X(t) =  *                                                                                               (8)

Формулы (7) и (8) представляют собой непериодический сигнал X(t) на интервале [ -∞;+∞ ]. Соответственно в частотной и временной областях данной формулы называется (7) – прямое и (8) – обратное преобразование Фурье.

Функции X(ω) характеризуют спектральный состав сигнала X(t) и называются спектральной плоскостью сигнала X(t), то есть, если с помощью ряда Фурье можно разложить периодические сигналы на бесконечное число гармоник с частотами, принимающими дискретное значение. То интегральное преобразование Фурье позволяет получить непериодический сигнал в виде бесконечного числа гармоник, частоты которых бесконечно близки.

---

Дата добавления: 2023-01-08; просмотров: 24; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!