Вычисление неопределенных интегралов.
⇐ ПредыдущаяСтр 2 из 2
| Функция f(x) | Первообразная F(x) | Пример |
| 0 | С | |
| 1 | х + С |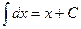 
|
| k – (число) | kx + C |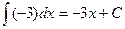 
|
| 
| 
|
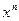
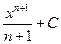
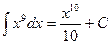
| x |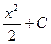 
| |
| 
| 
|
| 
| 
|
| 
| |
| 
| |
| 
| |
| 
| |
| 
| 
|
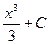
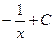
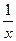
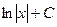
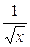
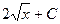
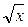
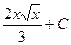
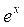
| sin x | - cos x +C | |
| cos x | sin x+C | |
| tg x +C |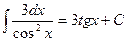 
|
| - ctg x+C |
Свойства неопределенных интегралов.
1. 
. Интегрирование и дифференцирование – взаимно обратные действия.
2. 
. Постоянный множитель можно вынести за знак интеграла.
3. 
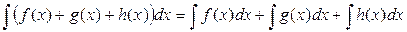. Интеграл суммы нескольких функций равен сумме интегралов этих функций.
4. 
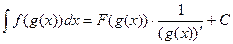. Интеграл сложной функции равен первообразной внешней функции, умноженной на выражение, обратное производной внутренней функции.
5. Интегрирование по частям: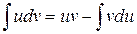 
.
Дата добавления: 2021-07-19; просмотров: 73; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!