Тригонометрические функции некоторых углов.

Требования к оформлению контрольной работы

По математике.

 

1. Контрольную работу следует выполнять в ученических тетрадях в клетку. На обложке тетради необходимо указать: название учебного заведения, название (номер) специальности; название и вариант контрольной работы; фамилию, имя, отчество и личный шифр студента.

 

2. На каждой странице необходимо оставить поля размером не менее 3-х см для оценки решения задач и методических указаний проверяющего работу.

 

3. Условия задач переписывать следует полностью.

 

4. Задачи в контрольной работе следует располагать по порядку и сопровождать их подробным решением.

 

5. В случае оформления контрольной работы в тетради необходимо использовать только ручку с черными или синими чернилами для описания решения задач, а графики должны выполняться с помощью линейки и карандаша.

 

6. Зачтенная контрольная работа является допуском к зачету.

 

7. Вариант контрольной работы выбирается в соответствии с последней цифрой номера зачетной книжки студента (если последняя цифра 0, то номер варианта 10) или по указанию преподавателя в соответствии с порядковым номером в журнале.

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 1

 

1. Даны матрицы: А = 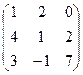     и В = 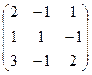 . Найти матрицу С = А^т · (В + 2А).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
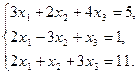
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
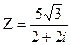4. Вычислить производную y ¢(х), если. y(х) = ln( sin2 x).

 

1. Вычислить неопределенный интеграл: .

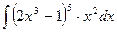6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

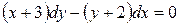, если у = 3 при х = 2.

 

 

______________________________________________________________________

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 2

1. Даны матрицы: А = 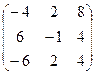  и В = 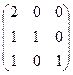. Найти матрицу С = (А – 2В) · А^т.
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
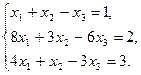
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
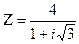4. Вычислить производную y ¢(х), если .

 

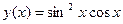1. Вычислить неопределенный интеграл: .

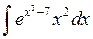6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

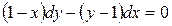,  если у = 3 при х = 2.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 3

1. Даны матрицы: А = 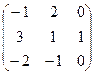    и В = 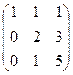. Найти матрицу Р = В × А + 3А^т .
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
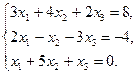
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
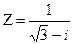4. Вычислить производную y ¢(х), если .

 

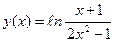1. Вычислить неопределенный интеграл: .

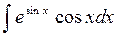6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

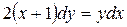, если у = 2 при х = 1.

 

_________________________________________________________________________

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 4

1. Даны матрицы: А = 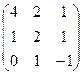    и В = 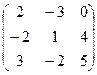. Найти матрицу Р = В^т · (2А – В).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
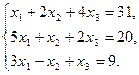
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
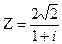4. Вычислить производную y ¢(х), если .

 

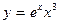1. Вычислить неопределенный интеграл: .

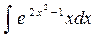6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

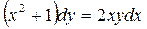  , если у = 2 при х = 1.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 5

1. Даны матрицы: А = 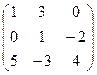    и В = 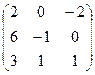. Найти матрицу Т = А × В + 2А^т;
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
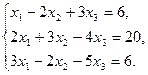
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
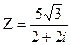4. Вычислить производную y ¢(х), если .

 

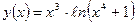1. Вычислить неопределенный интеграл: .

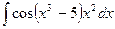6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

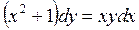, если у = 2 при х = .

 

__________________________________________________________________________

 

 

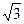Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 6

1. Даны матрицы: А = 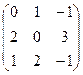     и В = 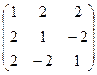. Найти матрицу М = А^т · (2А + В).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формула Крамера и методом Гаусса:  
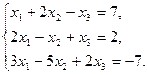
3. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
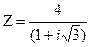4. Вычислить производную y ¢(х), если  .

 

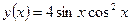1. Вычислить неопределенный интеграл: .

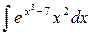6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

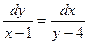  , если у = 4 при х = 0.

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 7

1. Даны матрицы: А = 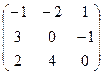 и В = 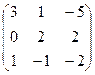. Найти матрицу К = В · А + (В^т - А^т).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формул Крамера и методом Гаусса:
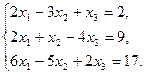
3. Записать число в трех формах: алгебраической, тригонометрической и показательной:
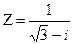
4. Вычислить производную y ¢(х), если .

 

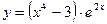1. Вычислить неопределенный интеграл: .

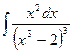6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

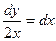  , если у = 6 при х = 1.

 __________________________________________________________________________

 

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 8

1. Даны матрицы: А = 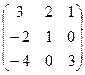    и В = 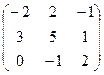. Найти матрицу М = А · В – 2А^т.
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:

 

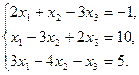
1. Записать число в трех формах: алгебраической, тригонометрической и показательной: .
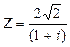2. Вычислить производную y ¢(х), если .

 

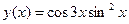1. Вычислить неопределенный интеграл: .

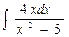6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 

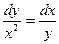  , если у = 2 при х = 0.

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 9

1. Даны матрицы: А = 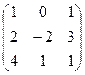 и В = 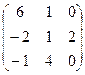. Найти матрицу С = А · В + (А^т – В).
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:
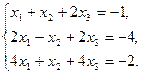
3.  Записать число в трех формах: алгебраической, тригонометрической и показательной: .
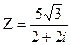4. Вычислить производную y ¢(х), если .

 

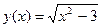1. Вычислить неопределенный интеграл: .

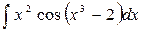6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 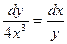  , если у = 1 при х = 0.

 

_____________________________________________________________________

 

 

Контрольная работа

по учебной дисциплине: «Математика»

для всех специальностей заочной формы обучения

 

Вариант 10

1. Даны матрицы: А = 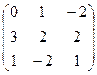   и В = 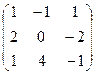. Найти матрицу К = 3В^т - А · В.
2. Дана система линейных уравнений. Решить ее двумя способами: при помощи формулам Крамера и методом Гаусса:
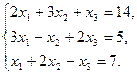
3.  Записать число в трех формах: алгебраической, тригонометрической и показательной: .
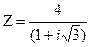4. Вычислить производную y ¢(х) ,  если .
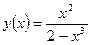5. Вычислить неопределенный интеграл: .

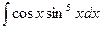6. Найти частное решение дифференциального уравнения с разделяющимися переменными: 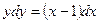  , если у = 4 при х = 0.

СПРАВОЧНЫЙ  МАТЕРИАЛ

Таблица производных

Функция	Производная
С	0
х	1
k x	k
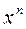
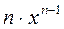
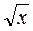
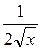
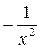
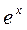
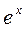
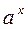
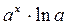
lnx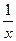
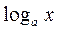
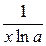
sinx	cosx
cosx	-sinx
tgx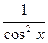
ctgx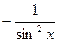

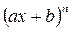
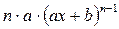
Правила дифференцирования

1.

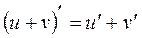
2.

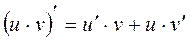
3.

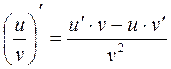
4. 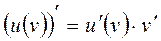      - сложная функция

 

 

Тригонометрические функции некоторых углов.

 

		I четверть				II четверть				III четверть				IV четверть
град	0°	30°	45°	60°	90°	120°	135°	150°	180°	210°	225°	240°	270°	300°	315°	330°	360°
рад	0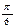
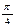
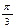
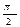
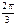
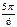
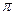
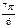
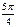
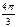
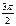
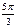
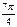
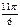
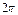
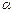
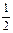
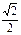
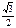
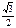
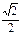
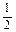
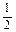
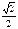
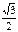
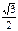
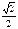
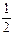
sin	0				1				0	-	-	-	-1	-	-	-	0
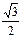
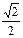
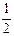
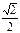
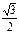
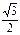
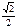
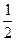
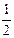
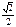
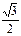
сos α	1				0	-	-	-	-1	-	-	-	0				1
tg α	0		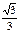1		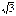нет		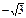-1	-	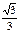0		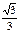1		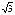нет		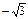-1	-	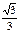0
сtg α	нет		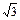1		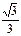0	-	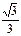-1		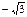нет		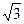1		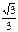0	-	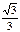-1		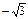нет

 

 

Помните, что:       ;            !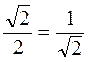

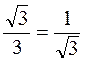Таблица первообразных.

---

Дата добавления: 2021-07-19; просмотров: 41; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!