Задания для самостоятельного решения:
И.С. Кравчук
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ В ПРИКЛАДНЫХ ПРИМЕРАХ И ЗАДАЧАХ
Учебно-методическое пособие
МОСКВА – 2017
УДК подходят: 519.852.61, 519.852.33
Рецензенты: А.А. Рогов, Е.В. Швед
В соответствии с учебной программой подготовки бакалавров технической специальности «Управление качеством» в учебно-методическое пособие включены задачи по основному разделу общего курса основ исследования операций – линейному программированию, в частности, подробно разобраны графический метод решения задач, симплекс-метод, метод искусственного базиса и транспортная задача.
Во всех разделах приведены краткие теоретические сведения и подробно разобраны примеры решения задач соответствующего типа.
Учебно-методическое пособие предназначено для студентов технических и экономических специальностей.
Оглавление
Введение. 4
1. Линейное программирование. 6
2. Графический метод решения задач линейного программирования. 8
2.1. Задания для самостоятельного решения: 14
3. Графический метод решения задач с несколькими переменными. 18
3.1. Задания для самостоятельного решения. 25
4. Симплекс-метод решения задач линейного программирования. 27
4.1. Задача линейного программирования в канонической форме. 27
4.2. Задача линейного программирования без начального базиса. 31
4.3. Задача линейного программирования с неограниченной целевой функцией. 35
|
|
|
4.4. Задача линейного программирования с двумя оптимальными решениями. 39
4.5. Задача линейного программирования с тремя оптимальными решениями. 41
4.6. Задачи для самостоятельного решения. 44
5. Метод искусственного базиса (М-метод) 48
5.1. Задача линейного программирования в канонической форме. 48
5.2. Задача линейного программирования в стандартном виде. 51
5.3. Задача линейного программирования с неограниченной целевой функцией. 54
5.4. Задача линейного программирования с двумя оптимальными решениями. 56
5.5. Задача линейного программирования с тремя оптимальными решениями. 58
5.6. Задача линейного программирования с несовместной системой ограничений. 60
5.7. Задания для самостоятельного решения. 62
6. Транспортная задача линейного программирования. 65
6.1. Транспортная задача с правильным балансом.. 67
6.2. Транспортная задача с неправильным балансом.. 78
6.3. Транспортная задача с ограничениями на пропускную способность. 85
6.4. Транспортная задача по критерию минимума времени. 91
6.5. Задания для самостоятельного решения. 96
Аттестационные задания по линейному программированию.. 103
Приложение 1. 122
Приложение 2. 124
|
|
|
Список литературы: 127
Введение
Математическим моделированием называется раздел математики, занимающийся методами решения различных задач, связанных с построением адекватных математических моделей и нахождением экстремумов функций при наличии ограничений на переменные. Математическое моделирование имеет ряд разделов: линейное, нелинейное, динамическое, выпуклое, стохастическое программирование и т.д.
Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднён по тем или иным причинам. Современная математика дает исключительно мощные и универсальные средства исследования. При построении математической модели изучаемого объекта или явления выделяют те его особенности, черты и детали, которые с одной стороны содержат более или менее полную информацию об объекте, а с другой допускают математическую формализацию. Математическая формализация означает, что особенностям и деталям объекта можно поставить в соответствие подходящие адекватные математические понятия: числа, функции, матрицы и так далее. Тогда связи и отношения, обнаруженные и предполагаемые в изучаемом объекте между отдельными его деталями и составными частями можно записать с помощью математических отношений: равенств, неравенств, уравнений. В результате получается математическое описание изучаемого процесса или явление, то есть его математическая модель.
|
|
|
Методами математического моделирования решаются следующие типовые задачи:
1) Задачи распределения ресурсов – возникают, когда существует определённый набор работ или операций, а имеющихся в наличии ресурсов для выполнения каждой из них наилучшим образом не хватает;
2) Задачи о планировании производства – возникают, когда необходимо определить такие объёмы выпуска продукции, чтобы получить максимальную прибыль;
3) Задачи управления запасами – заключаются в минимизации суммы ожидаемых затрат, связанных с хранением увеличивающихся запасов; и потерь, обусловленных их отсутствием в случае необходимости;
4) Задачи организации обслуживания оборудования – к ним относятся задачи назначения времени проведения проверок исправности оборудования, проведения профилактического обслуживания, выбора оптимального количества запасных частей;
5) Задачи массового обслуживания – рассматривают вопросы образования и функционирования очередей. Под очередью подразумевается линейная цепочка выстроившихся объектов (заявок), которые ожидают поступления в обслуживающее устройство (канал);
|
|
|
6) Задачи анализа рисков – прогнозируют вероятности возникновения рисков, связанных с инвестициями. Основные проблемы – измерение риска и определение допустимого уровня риска;
7) Транспортные задачи – связаны с составлением оптимального плана грузоперевозок с целью уменьшения затрат;
8) Задачи покрытия – возникают при планировании размещения объектов инфраструктуры с покрытием определённых зон;
9) Игровые задачи – связаны с поиском компромисса и выбором оптимальных стратегий игры в условиях конфликтных ситуаций и др.[1]
В настоящем учебно-методическом пособии рассматривается один из разделов математического моделирования – линейное программирование. Отличие методов линейного программирования от известных методов математического программирования обусловлено своеобразием целевых функций и областей их определения. Данный раздел математики получил название программирование в связи с тем, что в результате решения рассматриваемых задач составляется программа – алгоритм решения задач.
1. Линейное программирование
Линейное программирование представляет собой раздел математики, изучающий методы нахождения экстремальных значений линейных функций в некотором п-мерном пространстве. Основой для решения задач линейного программирования являются математические модели.
Математической моделью задачи линейного программирования называется совокупность соотношений, описывающих какой-либо процесс. Для составления математической модели необходимо:
1) Выбрать переменные задачи;
2) Составить систему ограничений для них;
3) Задать целевую функцию.[2]
Математическая модель (1.1) в общем виде выглядит следующим образом:
(1.1)
где 
– целевая функция – функция переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти;
– переменные задачи – это величины, которые характеризуют процесс. Обычно они записываются в виде вектора-строки 
;
Система ограничений – это совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических (технических) условий;
Опорным планом (допустимым решением) называется любой п-мерный вектор 
, удовлетворяющий системе ограничений и условиям неотрицательности, т.к. экономические задачи работают с физическими величинами. Множество всех допустимых решений задачи образует область (многоугольник) допустимых решений;
Оптимальным решением задачи называется такой опорный план, при котором целевая функция достигает экстремума.
Построение математической модели для задачи использования ресурсов:
Для изготовления п видов продукции используется т видов ресурсов (сырья). Известны: 
– запасы каждого i-го вида ресурса; 
- затраты каждого i-го вида ресурса на производство единицы объёма j-го вида продукции. Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы.
Введём вектор переменных задачи 
, где 
- объём производства j-го вида продукции. Затраты i-го вида ресурса на изготовление данного объёма xj продукции равны 
, поэтому ограничение на использование этого ресурса на производство всех видов продукции имеет вид: 
Прибыль от реализации j-го вида продукции равна 
и математическая модель данной задачи (1.2) имеет вид[1]:
(1.2)
ПРИМЕР № 1: При производстве двух видов продукции используется три вида сырья. Требуется составить план выпуска продукции (математическую модель), обеспечивающий максимальную прибыль. Исходные данные приведены в табл. 1.1:
Таблица 1.1
| Запасы сырья, ед. | Расход сырья на единицу продукции | |
| Продукция № 1 | Продукция № 2 | |
| 10 | 2 | 1 |
| 15 | 1 | 0,5 |
| 30 | 4 | 3 |
| Прибыль, у.е. | 70 | 90 |
Математическая модель данной задачи будет следующей:
ПРИМЕР № 2: Вагоностроительному заводу требуется сталь с содержанием углерода не более 1,3% и с долей легирующих элементов не более 8%. Завод закупает три сорта стали А, В, С с известным содержанием примесей. В какой пропорции нужно переплавить исходные продукты А, В, С чтобы сталь удовлетворяла ограничениям на содержание примесей и имела минимальную стоимость? Содержание примесей и цена исходных продуктов приведены в таблице (табл. 1.2):
Таблица 1.2
| Цена 1 т, у.е. | Содержание, % | Марка стали | |
| Углерод | Легир. элементы | ||
| 1200 | 1,2 | 4 | А |
| 1350 | 1,5 | 5 | В |
| 1700 | 2,1 | 13 | С |
Математическая модель данной задачи будет выглядеть следующим образом:
2. Графический метод решения задач линейного программирования
Этот метод используется для решения задач с двумя переменными и некоторых задач с большим количеством переменных при выполнении определённых условий. Он основывается на возможности графического изображения области допустимых решений задачи и нахождении среди них оптимального решения. Алгоритм графического метода решения включает в себя следующие основные этапы:
1) Построение множества (области) допустимых решений, которое основывается на том факте, что уравнение вида 
является уравнением прямой линии на плоскости и разделяет её на две полуплоскости: верхнюю (если знак неравенства «≥») и нижнюю (если знак неравенства «≤»). Множество допустимых решений – это замкнутый или открытый многоугольник. Если область допустимых решений является пустым множеством (в случае противоречивости неравенств системы ограничений), то задача не имеет решения ввиду несовместности системы ограничений.
2) Построение линии уровня (опорной прямой) для целевой функции и вектора нормали 
. Линией уровня называется прямая, в точках которой целевая функция 
постоянна. Уравнение линии уровня имеет вид: 
Опорной прямой называется линия уровня, относительно которой многоугольник решений находится в одной из полуплоскостей и которая имеет хотя бы одну общую точку с ним. Если многоугольник решений замкнут, то независимо от вида целевой функции имеется две опорных прямых. Если же область допустимых решений не замкнута, то в зависимости от направления нормали линий уровня, она может иметь как две, так и одну опорную прямую.
3) Нахождение экстремального значения целевой функции, которое базируется на том факте, что вектор нормали указывает направление возрастания целевой функции (соответственно, противоположный вектор указывает направление убывания функции). Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать в направлении их нормали, и убывают при перемещении линии уровня в противоположном направлении. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
4) Если задача имеет оптимальное решение, то для его нахождения совместно решаются уравнения прямых, ограничивающих многоугольник решений и пересекающихся с опорной прямой: 
Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением в этом случае является любая точка на прямой, соединяющей эти угловые точки.[1]
5) После нахождения оптимальных решений вычисляется значение целевой функции при этих решениях.
ПРИМЕР № 1: Найти экстремум целевой функции
при заданной системе ограничений:
Алгоритм решения задачи графическим методом:
1) Выражаем 
через 
в системе ограничений и нумеруем неравенства:
2) Строим графики системы ограничений и находим многоугольник решений (рис. 2.1).
3) Строим вектор нормали 
по коэффициентам переменных из целевой функции.
4) Строим опорную прямую (линию нулевого уровня) перпендикулярно вектору нормали.
5) Для нахождения максимума целевой функции двигаем опорную прямую по направлению вектора нормали до последней точки пересечения с многоугольником решений. Для нахождения минимума – двигаем опорную прямую в противоположном направлении (против стрелки) вектора нормали.
6) Находим координаты этой точки, приравнивая пересекающиеся в ней прямые №2 и №4. Это и будет оптимальным решением задачи:
Рисунок 2.1. Многоугольник решений.
7) Подставляем найденное оптимальное решение в целевую функцию: 
.
8) Ответ: 
ПРИМЕР № 2: Найти экстремум целевой функции при заданной системе ограничений: 
Решение
1) Выражаем через 
в системе ограничений:
2) Строим графики системы ограничений (рис. 2.2):
Рисунок 2.2. Графики системы ограничений.
3) Ответ: задача не имеет решения, т.к. система ограничений несовместна.
ПРИМЕР № 3: Из Москвы в Санкт-Петербург ежедневно отправляются скорые и пассажирские поезда. Наличный парк вагонов разных типов, из которых можно комплектовать данные поезда, и количества пассажиров, вмещающихся в каждом типе вагонов, приведены в таблице (табл. 2.1):
Таблица 2.1
| Тип вагона | Кол-во вагонов в поезде, шт | Кол-во мест в вагоне | Кол-во вагонов в парке | |
| скором | пасс. | |||
| Багажный | 1 | 1 | - | 12 |
| Почтовый | 1 | - | - | 8 |
| Плацкартный | 5 | 8 | 58 | 81 |
| Купейный | 6 | 4 | 40 | 70 |
| Спальный | 3 | 1 | 32 | 26 |
Требуется определить количества скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.[1]
Решение:
1) Определяем максимальные количества перевозимых пассажиров в скором и пассажирском поездах:
2) Составляем математическую модель задачи:
3) Выражаем через в системе ограничений и нумеруем каждое неравенство:
4) Строим графики системы ограничений и находим многоугольник решений задачи (рис. 2.3).
5) Наносим на график вектор нормали 
и перпендикулярную ему линию уровня L. Так как задача решается на поиск максимума целевой функции, двигаем линию уровня по направлению вектора нормали до последней точки (точек) пересечения с многоугольником решений. Этими точками, подозреваемыми на экстремум, являются точки 
, лежащие, соответственно, на пересечениях прямых (1)-(3) и (1)-(5).
Рисунок 2.3. Многоугольник решений задачи.
6) Находим координаты точек, подозреваемых на экстремум, приравнивая уравнения пересекающихся в них прямых:
Для точки 
:
Для точки 
:
7) Вычисляем значения целевой функции для решений , и сравниваем их:
Как видно из сравнения, 7722>7662 ⇒ 
, следовательно, 
является оптимальным решением данной задачи.
Ответ: 
.
Задания для самостоятельного решения:
1) На прядильно-ткацком комбинате для производства двух новых видов пряжи используется три типа сырья: шерсть, акрил и хлопок. В табл. 2.1.1 указаны нормы расхода сырья, его общее количество и прибыль от реализации 1 тонны пряжи каждого вида. Требуется составить такой план производства пряжи, чтобы суммарная прибыль была максимальной.[5]
Таблица 2.1.1
| Тип сырья | Нормы расхода сырья на 1 тонну пряжи, т | Количество сырья на складе, т | |
| Вид 1 | Вид 2 | ||
| Шерсть | 0,5 | 0,2 | 600 |
| Акрил | 0,1 | 0,6 | 620 |
| Хлопок | 0,4 | 0,2 | 500 |
| Прибыль, у.е. | 1100 | 900 | |
Математическая модель задачи имеет вид:
Ответ: Максимальное значение прибыли составит 1690000 у.е. при выпуске пряжи 1-го вида в количестве 800 т, пряжи 2-го вида в количестве 900 т., т.е. 
2) Нефтеперерабатывающий завод может использовать две различные технологии перегонки нефти для производства бензина, керосина и дизельного топлива. Стоимость 1 тонны сырой нефти составляет 22000 у.е. В табл. 2.1.2 приведены данные, показывающие выход продукции, отходы, издержки производства и загрузку оборудования в расчёте на 1 т переработанной нефти, а также стоимость 1 т готовой продукции и объём заказа от дилера (который необходимо обеспечить). Ресурс оборудования составляет 92 машино-часа в сутки. Все отходы должны пройти через очистные сооружения, производительность которых составляет 130 т в сутки. Требуется составить производственный план, обеспечивающий максимальную прибыль, причём без перепроизводства керосина.[5]
Таблица 2.1.2
| Наименование продукции | Выход готовой продукции, т | Стоимость 1 тонны готового продукта, у.е. | Объём заказа от дилера, т | |
| Технология 1 | Технология 2 | |||
| Бензин | 0,6 | 0,3 | 30000 | 200 |
| Керосин | 0,1 | 0,3 | 40000 | 50 |
| Дизельное топливо | 0,2 | 0,3 | 35000 | 50 |
| Отходы | 0,1 | 0,1 | - | - |
| Издержки производства, у.е. | 3000 | 2000 | - | - |
| Загрузка оборудования, маш.-ч. | 0,2 | 0,1 | - | - |
Математическая модель задачи имеет вид:
Ответ: 
, где, соответственно, 452 и 16 тонн переработанной нефти по обеим технологиям.
3) Перед проектировщиками автомобиля поставлена задача сконструировать самый дешёвый кузов, используя листовой металл, стекло и пластик. Общая поверхность кузова (вместе с дверьми и окнами) должна составить 14 м2, из них не менее 4 м2 и не более 5 м2 следует отвести под стекло. Общая масса кузова не должна превышать 150 кг. Основные характеристики материалов приведены в табл. 2.1.3.
Сколько металла, стекла и пластика должен использовать наилучший проект?[5]
Таблица 2.1.3
| Характеристики | Материалы | ||
| Металл | Стекло | Пластик | |
| Стоимость 1 м2, у.е. | 25 | 20 | 40 |
| Масса 1 м2, кг | 15 | 9 | 3 |
Математическая модель задачи имеет вид:
Ответ: Наилучший проект должен использовать в конструкции 6,5 м2 металла, 5 м2 стекла и 2,5 м2 пластика. При этом его стоимость будет равна 362,5 у.е., т.е 
4) Чайная компания выпускает чай двух сортов – «Традиционный» и «Отборный», смешивая три ингредиента: индийский, китайский и цейлонский чаи. В табл. 2.1.4 приведены технологические нормы расхода ингредиентов, объёмы запасов каждого ингредиента и прибыль от реализации 1 кг чая каждого сорта. Требуется составить оптимальный план расфасовки ингредиентов с целью максимизации суммарной прибыли.[5]
Таблица 2.1.4
| Ингредиенты | Нормы расхода, кг | Объёмы запасов, кг | |
| Традиционный | Отборный | ||
| Индийский чай | 0,5 | 0,2 | 600 |
| Китайский чай | 0,2 | 0,6 | 870 |
| Цейлонский чай | 0,3 | 0,2 | 430 |
| Прибыль, у.е./кг | 3200 | 2900 | |
Математическая модель задачи имеет вид:
Ответ: При заданных условиях чайная компания получит максимальную прибыль в размере 5545000 у.е., если выпустит 600 кг чая «Традиционный» и 1250 кг чая «Отборный», т.е. 
5) 
Ответ: 
6) 
Ответ: 
7) 
Ответ: 
8) 
Ответ: Система ограничений несовместна.
9) 
Ответ: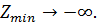 
10) 
Ответ: 
11) 
Ответ: 
12) 
Ответ:
3. Графический метод решения задач с несколькими переменными
Графический метод даёт наглядное решение, но он позволяет работать только с двумя переменными. Поэтому, если в исходной задаче п переменных и она представлена в канонической форме, то сначала нужно её упростить до двух переменных с помощью элементарных преобразований Жордана-Гаусса,
а затем решить графическим методом.
Каноническая форма задачи линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть произвольно изменяющимися. В том случае, когда все ограничения задачи являются уравнениями и все переменные неотрицательны, форму записи задачи линейного программирования называют канонической. Каноническая форма задачи линейного программирования имеет вид (3.1):
(3.1)
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Любая переменная 
, на которую не наложено условие неотрицательности, заменяется разностью двух других неотрицательных переменных: 
Однако при составлении математических моделей задач ограничения в основном формируются в виде системы неравенств, поэтому необходимо уметь переходить от системы неравенств к системе уравнений.[1]
Алгоритм перевода задачи линейного программирования в каноническую форму рассмотрим на следующем примере.
ПРИМЕР № 1: Перевести задачу линейного программирования в каноническую форму записи: 
Для перехода от неравенств к уравнениям нужно ввести в систему ограничений дополнительные переменные, причём:
1) В неравенство вида 
нужно добавлять дополнительную переменную 
(т.е. вводить её в систему ограничений с коэффициентом «+1»);
2) Из неравенства вида 
нужно вычитать дополнительную переменную (т.е. вводить её в систему ограничений с коэффициентом «–1»).
3) В целевую функцию дополнительные переменные входят с нулевыми коэффициентами, чтобы не изменять её значение.
Учитывая вышесказанное, переводим задачу в каноническую форму:
Таким образом, каноническая форма данной задачи имеет вид:
Симметричная форма задачи линейного программирования
При решении некоторых задач линейного программирования возникает необходимость перехода от канонической формы к симметричной, в которой за счёт исключения базиса остаются только две переменные. Симметричная форма позволяет упростить исходную задачу с несколькими переменными всего до двух, а затем решить её графическим методом.[1]
ПРИМЕР № 2: Перевести задачу линейного программирования из канонической формы в симметричную:
Записываем систему ограничений задачи в виде расширенной матрицы и выносим коэффициенты целевой функции отдельной строкой. Далее методом Жордана-Гаусса приводим систему ограничений к разрешённому виду (табл. 3.1).
В результате преобразований каноническая форма задачи принимает следующий вид:
Таблица 3.1
Далее в строке целевой функции число (–9) переносим в левую часть, меняя знак, а из системы ограничений исключаем базисные переменные x 2 и x 3, таким образом меняя уравнения на неравенства:
Это и есть симметричная форма данной задачи линейного программирования, упрощённая до двух переменных.
ПРИМЕР № 3: Решить задачу линейного программирования графическим методом: 
Алгоритм решения задач графическим методом с п переменными:
1) Приводим задачу к симметричному виду (табл. 3.2):
2) В результате преобразований каноническая форма задачи примет следующий вид:
Таблица 3.2
3) Полученный базис, состоящий из векторов 
необходимо исключить из системы ограничений и, таким образом, привести её к симметричной форме с двумя переменными: 
4) Далее можно решать задачу обычным графическим методом для двух переменных:
Вектор нормали имеет координаты: 
5) Строим графики системы ограничений задачи (рис. 3.1):
Рисунок 3.1. Графики системы ограничений
Целевая функция не ограничена, т.к. многоугольник решений не замкнут, и линия уровня уходит в бесконечность.
Ответ: 
ПРИМЕР № 4: Решить задачу линейного программирования графическим методом:
Решение:
1) Приводим задачу к симметричному виду (табл. 3.3):
2) В результате преобразований каноническая форма задачи принимает следующий вид:
3) Симметричная форма записи данной задачи (после исключения базиса) имеет вид:
Таблица 3.3
4) Далее решаем задачу графическим методом для двух переменных. Выражаем переменную х2 через х1, находим координаты вектора нормали и строим графики системы ограничений (рис. 3.2):
Рисунок 3.2. Графики системы ограничений.
5) Точки, подозреваемые на экстремум – точки 
, лежащие, соответственно, на пересечениях прямых (2)-(3) и (1)-(2).Находим координаты этих точек, приравнивая уравнения пересекающихся в них прямых:
Для точки :
Для точки :
6) Вычисляем значения целевой функции для решений , и сравниваем их:
Как видно из сравнения, 60=60 ⇒ 
, следовательно, 
7) Далее подставляем оптимальные решения этой вспомогательной задачи в систему ограничений преобразованной канонической формы для того, чтобы перейти к оптимальному решению исходной задачи, состоящему из четырёх переменных.
Для решения :
Для решения :
Ответ: 
.
Дата добавления: 2020-11-15; просмотров: 287; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!