ТЕОРЕМА ЛАГРАНЖА ДЛЯ ГРУПП, СЛЕДСТВИЯ ИЗ НЕЁ.
Пусть дана конечная группа порядка n, для определения мультипликативная.
А={ 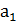 ,
, 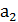 ,…,
,…, 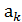 }.
}.
Теорема Лагранжа.
Для любой конечной группы порядок любой её подгруппы является делителем порядка самой группы.
Доказательство:
Наша цель доказать, что n делится нацело k.
Пример, |G|=12, | 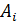 |:1, 2, 3, 4, 6, 12.
|:1, 2, 3, 4, 6, 12.
Запишем левостороннее разложение группы G по подгруппе А.
G= 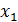 AÈ
AÈ 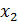 AÈ…È
AÈ…È 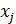 A, j - индекс разложении, то есть количество разложения смежных классов.
A, j - индекс разложении, то есть количество разложения смежных классов.
По свойству 4 смежных классов, любой левый смежный класс состоит из k различных элементов группы G, так как смежных классов j, то всего в разложении будет k-j элементов.
По условию, число элементов в группе равно n, получили равенство n=k-j ⇨ n делится нацело k.
Ч.т.д.
Следствие 1. Порядок любого элемента группы G, где G конечная группа является делителем порядка самой группы.
Доказательство: Действительно, порядок любого элемента группы G совпадает с порядком порожденной им циклической подгруппы по теореме Лагранжа следствие доказано.
Следствие 2. Любая группа простого порядка p является циклической.
Доказательство: Действительно, с помощью каждого элемента группы G можно построить циклическую подгруппу данной группы.
Будет только одна подгруппа первого порядка порожденная нейтральным элементом. Все остальные подгруппы будут иметь порядок Р, так как Р – простое число, а по теореме Лагранжа порядок группы является делителем порядка группы.
Получим, что сама группа совпадает с циклическими подгруппами, следовательно является циклической.
НОРМАЛЬНЫЕ ДЕЛИТЕЛИ ГРУППЫ.КРИТЕРИЙ НОРМАЛЬНОГО ДЕЛИТЕЛЯ.
Пусть дана для определенности мультипликативная группа G и пусть А – произвольно выбранная подгруппа группы G.
Определение 1.
Подгруппа А группы G называется нормальным делителем группы G если, левосторонне разложение группы G по подгруппе А совпадает с правосторонним разложением группы G по подгруппе А.
Если группа G – абелева, то любая её подгруппа является нормальным делителем группы G.
Определение 2.
Подгруппа А группы G называется нормальным делителем группы G, если "xÎG: x⋅A=A⋅x.
Если подгруппа А группы G является нормальным делителем группы G, то "xÎG и "аÎG, $  ,
, 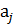 ÎA:
ÎA:
1. x⋅a= 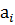 ⋅x;
⋅x;
2. a⋅x=x⋅ 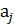 ;
;
Возьмем "аÎG, и пусть "xÎG, элементы вида 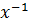 ⋅a⋅x называются сопряженными элементами для элемента а.
⋅a⋅x называются сопряженными элементами для элемента а.
Заметим, что элементы вида x⋅a⋅ 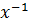 так же будут сопряженными с элементом а.
так же будут сопряженными с элементом а.
x⋅a⋅ 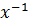 =
= 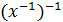 ⋅a⋅x.
⋅a⋅x.
Справедлив критерий нормального делителя:
Подгруппа А группы G будет нормальным делителем группы G тогда и только тогда когда подгруппа А вместе с любым а будет содержать все элементы ему сопряженные.
Доказательство:
I. Необходимость;
Дано: А – нормальный делитель группы G.
Доказать: "аÎА, 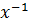 ⋅a⋅xÎА, "xÎG.
⋅a⋅xÎА, "xÎG.
Доказательство:
Так как А – нормальный делитель группы G.
x⋅a=  ⋅x; a⋅x=x⋅
⋅x; a⋅x=x⋅  , где
, где  ,
,  ÎA.
ÎA.
Воспользуемся вторым равенством и умножим обе части на 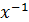 слева.
слева.
Заметим, что 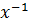 ÎG, так как G – группа, получим:
ÎG, так как G – группа, получим:
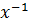 ⋅(a⋅x)=
⋅(a⋅x)= 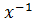 ⋅x⋅
⋅x⋅ 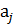 ,
,
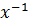 ⋅a⋅x=(
⋅a⋅x=( 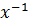 ⋅ x)⋅
⋅ x)⋅  ,
,
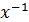 ⋅a⋅x=
⋅a⋅x=  , где
, где  ÎА ⇨
ÎА ⇨ 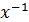 ⋅a⋅xÎА.
⋅a⋅xÎА.
II. Достаточность.
Дано: "аÎА, 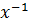 ⋅a⋅xÎА, "xÎG.
⋅a⋅xÎА, "xÎG.
Доказать: А – нормальный делитель группы G.
Доказательство:
Чтобы доказать, что А – нормальный делитель группы G, достаточно доказать выполнимость двух равенств определяющих нормальный делитель.
Так как 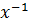 ⋅a⋅xÎА, то обозначим
⋅a⋅xÎА, то обозначим 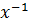 ⋅a⋅x=
⋅a⋅x= 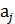 , где
, где 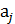 ÎА.
ÎА.
Умножим обе части последнего равенства на xÎG слева:
x⋅( 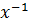 ⋅a⋅x)= x⋅
⋅a⋅x)= x⋅  ,
,
(x⋅ 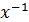 )⋅a⋅x= x⋅
)⋅a⋅x= x⋅  ,
,
a⋅x= x⋅ 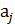 – выполнилось равенство 2.
– выполнилось равенство 2.
Заметим, что 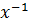 ⋅a⋅x сопряжен с элементом x, "xÎG, то
⋅a⋅x сопряжен с элементом x, "xÎG, то 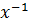 ⋅a⋅xÎА.
⋅a⋅xÎА.
Тогда 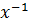 ⋅a⋅x=
⋅a⋅x=  , где
, где  ÎА.
ÎА.
Умножим обе части равенств на x справа: ( 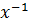 ⋅a⋅x)⋅x=
⋅a⋅x)⋅x= 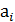 ⋅x,
⋅x,
a⋅x=  ⋅x – выполнилось 1 равенство.
⋅x – выполнилось 1 равенство.
Значит А – нормальный делитель группы G.
Дата добавления: 2018-11-24; просмотров: 315; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
