Производные и дифференциалы высших порядков.
дифференцируема в точке 
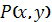следовательно, существует непрерывность.
, 
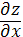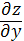каждая из функций также дифференцируема в точке P это значит мы можем найти по 2 частной производной
,
,
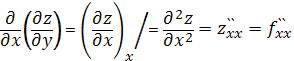
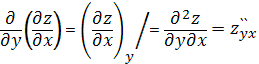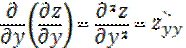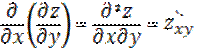
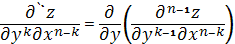
Пример 1. Найти частную производную 2-го порядка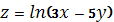 
, 
, 
, 
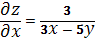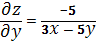
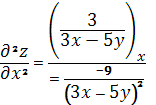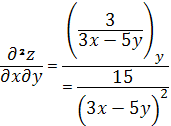
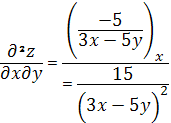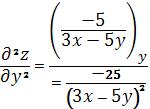
Th. Если имеет в точке P непрерывные смешанные частные производные 2-го порядка, то они равны:
, 
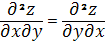
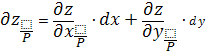
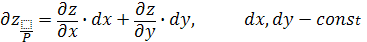
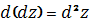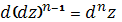
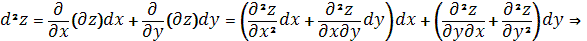
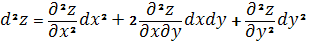
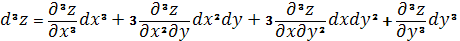
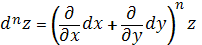
Дата добавления: 2015-12-18; просмотров: 17; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!