Лекция 3. Математические модели сообщений и сигналов. Спектральные представления сигналов

 

Содержание лекции:

- теория ортогональных сигналов. Ортогональные сигналы и обобщенные ряды Фурье. Примеры ортонормированных базисов. Периодические сигналы и ряды Фурье. Ряд Фурье.Спектральная диаграмма периодического сигнала.Комплексная форма ряда Фурье.

 

Цель лекции:

- возможность представлять сигналы посредством обобщенных рядов Фурье. Найти спектральное разложение периодического сигнала

 

Двасигнала и и v называются ортогональными, если их ска­лярное произведение, а значит, и взаимная энергия равны нулю

( u , v )= u ( t ) v { t ) dt =0. (3.1)

Пусть H— гильбертово пространство сигналов с конеч­ным значением энергии (линейное пространство со скалярным произведением, полное в том смысле, что оно содержит в себе все пре­дельные точки любых сходящихся последовательностей век­торов из этого пространства). Эти сигналы определены на отрезке времени [t₁, t₂], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функ­ций { }, ортогональных друг другу и обла­дающих единичными нормами

(ui,uj) = 1, если i=j (3.2)

0, если i j.

Говорят, что при этом в пространстве сигналов задан ортонормированный базис. Разложим произвольный сигнал s ( t ) 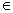H в ряд

s(t)= . (3.3)

Представление (3.3) называется обобщенным рядом Фурье сигнала s ( t ) в выбранном базисе. Коэффициенты данного ряда находят следующим образом. Возьмем базисную функцию и _k произвольным номером k , умножим на нее обе части равенства (1.27) и затем про­интегрируем результаты по времени

. (3.4)

Ввиду ортонормированности базиса в правой части равен­ства (3.4) останется только член суммы с номером i = k , поэтому

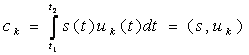. (3.5)

Теперь есть возможность характеризовать сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье с_k.

Ортонормированная система гармонических функций. На отрезке [0,Т] система тригонометрических функций с крат­ными частотами, дополненная постоянным сигналом образует ортонормированный базис.

(3.6)

Ортонормированная система функций Уолша. В последнее время под влиянием методов обработки дискретных сигна­лов большое внимание уделяют ортонормированной системе функций Уолша, которые на отрезке своего существования [-Т/2, Т/2] принимают лишь значения ±1.

Введем безразмерное время и будем обозначать k-ю функцию Уолша, как это принято, символом wal (k, 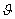). Идею построения этой системы легко усмотреть из рисунка 3.1, на котором изображены графики нескольких первых функций Уолша. Очевидна нормированность функций Уолша при любом значении k: ||wal (k, 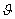)||2=

Рисунок 3.1 - Графики нескольких первых функций Уолша

 

Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно.

Разложение сигнала с конечной энергией, заданного на отрезке времени [-Т/2,Т/2], в обобщенный ряд Фурье по функциям Уолша имеет вид

s ( t )= 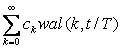. (3.7)

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов для радиотехники обусловлено рядом причин:

а) гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями;

б) техника генерирования гармонических сигналов относительно проста.

Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение этого сигнала. Отдельные гармонические компоненты сигнала образуют его спектр.

Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:

s ( t ) = s ( t ± пТ), п = 1, 2, ... (3.8)

Здесь T - период сигнала.

В электросвязи наибольшее применение находят одиночные импульсы или их периодическая последовательность, форма ко­торых приближается к прямоугольной. Для периодической после­довательности импульсов, кроме перечисленных выше параметров, вводится понятие скважности, определяемой как отношение пе­риода к длительности импульса: S = Tlt _и .

Зададим на отрезке времени [-T/2, T/2] ортонормированный базис (3.6).

Любая функция u_m из этого базиса удовлетворяет условию периодичности (3.8). Поэтому, выполнив ортогональное разложение сигнала s (t) в этом базисе, т. е. вычислив коэффициенты C_m=(s,u_m), получим спектральное разложение

(3.9)

справедливое на всей бесконечности оси времени.

Ряд вида (3.9) называется рядом Фурье данного сигнала. Введем основную частоту ω₁=2π/T последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения, запишем ряд Фурье для периодического сигнала

(3.10)

с коэффициентами

,

, (3.11)

.

Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ω_n = nω₁ (n = 1, 2, 3, ...), кратными основной частоте последовательности. Каждую гармонику можно описать ее амплитудой A_n и начальной фазой φ_n. Для этого коэффициенты ряда Фурье следует записать в виде

a_n=A_ncosφ_n, b_n=A_nsinφ_n так, что

A_n= , tgφ_n=b_n/a_n.

Подставив эти выражения в (3.10), получим другую, эквивалентную форму ряда Фурье

. (3.12)

Спектральная диаграмма периодического сигнала - графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают: а) амплитудные и б) фазовые спектральные диаграммы (см. рисунок 3.2). Здесь по горизонтальной оси в некотором масштабе отложены частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы.

Рисунок 3.2 - Спектральные диаграммы некоторого периодического сигнала

 

Спектральное разложение периодического сигнала можно выполнить, используя систему базисных функций, состоящую из экспонент с мнимыми показателями (3.13)

Легко видеть, что функции этой системы периодичны с периодом Т и ортонормированы на отрезке времени [-Т/2, Т/2], так как

Ряд Фурье произвольного периодического сигнала в дан­ном случае принимает вид

(3.14)

. (3.15)

Выражение (3.14) представляет собой ряд Фурье в комплекс­ной форме.

---

Дата добавления: 2018-09-20; просмотров: 305; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!