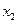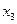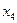Алгоритм решения транспортной задачи
1) Проверить выполнение условия (2.3). Если оно не выполняется, то перейти к соответствующей закрытой матричной модели ТЗ.
2) Построить невырожденный начальный опорный план (метод «минимального элемента», метод «северо-западного угла» или метод Фогеля).
3) Методом потенциалов проверить найденный план на оптимальность.
4) Если план оптимален, то задача решена.
5) Если план оптимален, но не единственен, то можно найти еще один оптимальный план.
6) Если пункты 4) – 5) алгоритма не выполняются, найти новый опорный план и перейти к пункту 3).
Замечание
При решении транспортной задачи с целевой функцией на максимум необходимо перейти к эквивалентной задаче с целевой функцией на минимум. Для этого целевую функцию нужно умножить на «–1» ( 
). Это означает, что все тарифы распределительной таблицы нужно взять с противоположным знаком. Решив задачу, нужно перейти к решению исходной задачи, т.е. полученное значение целевой функции умножить на «–1» ( 
).
Построение опорных планов, а также преобразование их будем производить непосредственно в распределительной таблице. Если в плане перевозок переменная отлична от нуля 
, то ее значение записываем в соответствующую клетку (l , k) и считаем ее занятой или базисной, если же 
, то клетку 
оставляем свободной.
Существует несколько методов построения начального опорного плана – это метод «минимального элемента», метод «северо-западного угла», метод Фогеля и другие.
|
|
|
Нахождение начального опорного плана методом
«минимального элемента»
Данный метод позволяет построить опорный план, который достаточно близок к оптимальному. Он состоит из ряда однотипных шагов, на каждом из которых заполняется максимально возможным значением только одна клетка таблицы, соответствующая минимальному тарифу, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Поставщик исключается из рассмотрения, если его запасы заканчиваются. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от него требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично поступают с потребителем.
Пример 2.2
По данным примера 2.1 найти начальный опорный план методом «минимального элемента».
Решение
Воспользуемся распределительной таблицей закрытой модели ТЗ (табл. 2.3). Наименьшие затраты на перевозку топлива соответствуют маршруту 
, поэтому заполним любую клетку столбца 
, например клетку (1,5) и 
. Таким образом, потребности в топливе потребителя удовлетворены и пятый столбец из рассмотрения исключаем, а в хранилище 
останется 70–10=60 т топлива. Просматриваем оставшиеся клетки таблицы. Наименьшие тарифы имеют клетки (2,4) и (3,3): 
. Заполняем любую из этих клеток, например клетку (2,4) и 
. Столбец 
исключаем, а в хранилище 
при этом останется 90–40=50 т топлива. Просматриваем оставшиеся клетки таблицы. Наименьший тариф имеет клетка (3,3). Заполним ее: 
и исключаем столбец 
, а в хранилище 
осталось 50–40=10 т топлива. Просматриваем оставшиеся клетки таблицы. Наименьший тариф имеет клетка (3,1): 
. Клетку (3,1) заполним 
и исключаем строку , а потребителю 
недостает 50–10=40 т топлива. Далее по величине тарифа заполним клетку (2,2), т.к. 
, при этом 
и исключаем строку 
, а потребителю 
недостает 70–50=20 т топлива. Далее по величине тарифа заполним клетку (1,2), т.к. 
и 
и исключаем столбец 
, а в хранилище осталось 60–20=40 т топлива. Заполним оставшуюся клетку (1,1): 
. Итак, в распределительной таблице найден невырожденный (число занятых клеток k = m + n–1=3+5–1=7) начальный опорный план (табл. 2.4).
|
|
|
Таблица 2.4
|
|
|
| Потребители | Запас топлива, т | ||||||||||
| Хранилища |
|
|
|
|
| ||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 | |||||
| 40 | 20 | 10 | |||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 | |||||
| 50 | 40 | ||||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 | |||||
| 10 | 40 | ||||||||||
| Потребность в топливе, т | 50 | 70 | 40 | 40 | 10 | 210 | |||||
или 
. Значение целевой функции на найденном начальном опорном плане (транспортные издержки для этого плана):
( усл. ден. ед.)
Нахождение начального опорного плана методом
«северо-западного угла»
Согласно данному методу запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.
Заполнение распределительной таблицы ТЗ начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель. При этом нулевые перевозки принято заносить в таблицу только в том случае, когда они попадают в клетку, подлежащую заполнению, т.е. в таблицу заносятся только базисные нули, остальные клетки с нулевыми перевозками остаются пустыми. При построении невырожденного опорного плана число занятых клеток должно быть k = m + n–1.
|
|
|
Необходимо иметь в виду, что метод северо-западного угла не учитывает тарифы перевозок, поэтому опорный план, построенный по данному методу, может быть далек от оптимального.
Пример 2.3
По данным примера 2.1 найти начальный опорный план методом «северо-западного угла».
Решение
Воспользуемся распределительной таблицей закрытой модели ТЗ (табл. 2.3).
Распределяем топливо из первого хранилища. Заполним клетку (1,1) максимально-возможным значением: 
. Таким образом, потребности в топливе потребителя 
удовлетворены и первый столбец из рассмотрения исключается, а в хранилище 
останется 70–50=20 т топлива. Теперь левой верхней (северо-западной) клеткой оставшейся части таблицы является клетка (1,2) и 
. Т.к. в первом хранилище топлива больше нет, то первая строка исключается, а потребителю недостает 70–20=50 т топлива.
Распределяем топливо из второго хранилища. Заполним клетку (2,2): 
. Столбец исключаем, а в хранилище осталось 90–50=40 т топлива. Теперь заполним клетку (2,3): 
и исключаем по своему усмотрению либо второго поставщика, либо третьего потребителя. Пусть исключили третьего потребителя. Тогда в хранилище осталось 40–40=0 т топлива. Теперь заполним клетку (2,4): 
и исключаем вторую строку.
Распределяем топливо из третьего хранилища. Теперь заполним клетку (3,4): 
. Столбец 
исключаем, а в хранилище осталось 50–40=10 т топлива. Незаполненной осталась одна клетка (3,5) и 
. Итак в распределительной таблице записан невырожденный (число занятых клеток k = m + n–1=3+5–1=7) начальный опорный план (табл. 2.5).
Таблица 2.5
| Потребители | Запас топлива, т | ||||||||||
| Хранилища |
|
|
|
|
| ||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 | |||||
| 50 | 20 | ||||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 | |||||
| 50 | 40 | 0 | |||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 | |||||
| 40 | 10 | ||||||||||
| Потребность в топливе, т | 50 | 70 | 40 | 40 | 10 | 210 | |||||
или 
. Значение целевой функции на найденном начальном опорном плане (транспортные издержки для этого плана):
( усл. ден. ед.)
Нахождение начального опорного плана методом Фогеля
Данный метод состоит из ряда однотипных шагов (этапов), на каждом из которых:
· для каждой линии (по строкам и столбцам) определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность (жирным шрифтом);
· в линии с наибольшей разностью заполняется максимально возможным значением клетка, соответствующая минимальному тарифу;
· исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Поставщик исключается из рассмотрения, если его запасы заканчиваются. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от него требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично поступают с потребителем.
Когда в процессе заполнения таблицы, на каком-то этапе незаполненными оказываются только клетки в одной линии, то их необходимо заполнить в порядке увеличения тарифов.
Данный метод позволяет построить опорный план, который достаточно близок к оптимальному, и зачастую может даже оказаться оптимальным.
Пример 2.4
По данным примера 2.1 найти начальный опорный план методом Фогеля.
Решение
Воспользуемся распределительной таблицей закрытой модели ТЗ (табл. 2.3).
На первом этапе максимальная разность «4» принадлежит столбцу 
. Заполняем клетку с минимальным тарифом в этом столбце. Это клетка (2,4) и . Столбец 
исключаем, а в хранилище 
при этом останется 90–40=50 т топлива.
На втором этапе максимальная разность «3» принадлежит строкам 
и 
. Выбираем любую из них, например, строку . Заполняем клетку с минимальным тарифом в этой строке. Это клетка (1,5) и 
. Столбец 
исключаем, а в хранилище 
при этом останется 70–10=60 т топлива.
На третьем этапе максимальная разность «2» принадлежит столбцам 
и . Выбираем любой из них, например, столбец . Заполняем клетку с минимальным тарифом в этом столбце. Это клетка (3,1) и 
. Исключаем по своему усмотрению либо третьего поставщика, либо первого потребителя. Пусть исключили первого потребителя. Тогда в хранилище 
осталось 50–50=0 т топлива.
На четвертом этапе максимальная разность «3» принадлежит строке . Заполняем клетку с минимальным тарифом в этой строке. Это клетка (3,3) и 
. Строку исключаем, а потребителю недостает 40–0=40 т топлива.
На пятом этапе максимальная разность «2» принадлежит строке и столбцу . Выбираем любую из этих линий, например, строку . Заполняем клетку с минимальным тарифом в этой строке. Это клетка (1,5) и 
. Строку исключаем, а потребителю недостает 70–50=20 т топлива.
Т.к. незаполненные клетки остались в одной линии (в строке клетки (1,2) и (1,3)), то заполняем их в порядке увеличения тарифов, т.е. сначала заполним клетку (1,3): 
, затем клетку (1,2) и 
.
Итак, в распределительной таблице найден невырожденный (число занятых клеток k = m + n–1=3+5–1=7) начальный опорный план (табл. 2.6).
Таблица 2.6
|
|
|
|
|
|
|
| Этапы | ||||||||||
|
| 1 | 2 | 3 | 4 | 5 | ||||||||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 | 3 | 3 | 1 | 1 | 1 | ||||||
| 20 | 40 | 10 | |||||||||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 | 1 | 3 | 1 | 2 | 2 | ||||||
| 50 | 40 | ||||||||||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 | 1 | 1 | 1 | 3 | – | ||||||
| 50 | 0 | ||||||||||||||||
|
| 50 | 70 | 40 | 40 | 10 | ||||||||||||
| Э т а п | 1 | 2 | 1 | 2 | 4 | 0 | |||||||||||
| 2 | 2 | 1 | 2 | – | 0 | ||||||||||||
| 3 | 2 | 1 | 2 | – | – | ||||||||||||
| 4 | – | 1 | 2 | – | – | ||||||||||||
| ы | 5 | – | 1 | 2 | – | – | |||||||||||
или 
. Значение целевой функции на найденном начальном опорном плане (транспортные издержки для этого плана):
( усл. ден. ед.)
Проверка на оптимальность невырожденного опорного плана методом потенциалов
1) Каждому поставщику поставим в соответствие потенциал 
, а каждому потребителю потенциал 
.
Тогда каждой занятой клетке будет соответствовать уравнение:
.
Так как всех занятых клеток должно быть m + n–1, то есть на единицу меньше числа потенциалов, то для нахождения 
необходимо решить систему из m + n–1 уравнений 
с m + n неизвестными. Система является линейно-зависимой и, чтобы найти частное решение, одному из потенциалов нужно присвоить произвольное числовое значение, тогда остальные потенциалы определяются однозначно. Для исследования плана на оптимальность для каждой свободной клетки считаем оценки по формуле:
;
а) если все оценки положительны, то найденный опорный план оптимален и единственен 
;
б) если наряду с положительными оценками встречаются и нулевые оценки 
, то найденный опорный план оптимален, но не единственен;
в) если оценка хотя бы одной свободной клетки отрицательна 
, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка с наименьшей оценкой. Например, для клеток 
имеем оценки 
. Здесь наиболее перспективной для загрузки является клетка 
.
Переход к новому опорному плану
План перевозок можно улучшить за счет загрузки свободной клетки с отрицательной оценкой. Для этого для наиболее перспективной для загрузки свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно присваиваются знаки: свободной клетке – плюс, следующей по (или против) часовой стрелке занятой клетке – минус, следующей – снова плюс и т.д. Из значений в клетках цикла помеченных знаком минус выбирается наименьшее количество груза, которое прибавляется к значениям клеток, помеченных знаком плюс и отнимается от значений, помеченных знаком минус.
Цикл пересчета
В общем случае цикл пересчета представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки одной линии (строки или столбца). В цикле всегда четное число клеток, причем только одна свободная, та относительно которой он составлен, остальные клетки цикла загружены. Для любой свободной клетки всегда можно построить единственный цикл.
Пример 2.5
По данным примера 2.1 исходя из начального опорного плана найденного в примере 2.2 решить транспортную задачу (найти оптимальный план перевозок и минимальные затраты на транспортировку всего топлива).
Решение
Воспользуемся распределительной таблицей, в которой найден начальный опорный план методом «минимального элемента» (табл. 2.4 и табл. 2.7).
Таблица 2.7
| Потребители | Запас топлива, т |
| ||||||||||
| Хранилища |
|
|
|
|
| |||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 |
| |||||
| 40 | 20 | 10 | ||||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 |
| |||||
| 50 | 40 | |||||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 |
| |||||
| 10 | 40 | |||||||||||
| Потребность в топливе, т | 50 | 70 | 40 | 40 | 10 | 210 | ||||||
|
|
|
|
|
| ||||||||
Для проверки найденного плана на оптимальность найдем потенциалы строк и столбцов (табл. 2.7), составив для каждой занятой клетки уравнение . При этом получим следующую систему уравнений:
Система является линейно-зависимой, для нахождения одного из частных решений присвоим одному из потенциалов любое числовое значение, например 
, и найдем значения остальных потенциалов:
Потенциалы можно находить непосредственно в распределительной таблице. Нужно присвоить какому-нибудь потенциалу любое числовое значение и по цепочке, используя уравнение , по занятым клеткам найти все остальные потенциалы (в табл. 2.8 указана очередность нахождения потенциалов, приняв ).
Таблица 2.8
| Потребители | Запас топлива, т |
| ||||||||||
| Хранилища |
|
|
|
|
| |||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 | 1)
| |||||
| 40 | – | 20 | + | 10 | ||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 | 6)
| |||||
| 50 | 40 | |||||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 | 5) | |||||
| 10 | + | 40 | – | |||||||||
| Потребность в топливе, т | 50 | 70 | 40 | 40 | 10 | 210 | ||||||
| 2) | 3) | 7) | 8) | 4) | ||||||||
Оценки свободных клеток найдем по формуле :
Так как среди оценок есть отрицательная ( 
), то найденный план не оптимален. Его можно улучшить путем загрузки этой клетки.
Составим цикл пересчета относительно клетки (1,3) и присвоим клеткам цикла знаки «+» и «–». Свободной клетке (1,3) присвоим знак «+», а дальше, по часовой стрелке, следующей клетке цикла (3,3) присвоим знак «–», затем клетке цикла (3,1) присвоим знак «+», далее клетке цикла (1,1) присвоим знак «–» (табл. 2.8).
Из клеток, помеченных знаком «–», выбираем наименьшее количество груза 
. Чтобы получить новый опорный план нужно прибавить значение 
к поставкам в клетках, помеченных знаком «+» и вычесть из поставок в клетках, помеченных знаком «–», нули при этом не записываются (табл. 2.9). Т.к. значение оказалось в двух клетках цикла (клети (1,1) и (3,3) табл. 2.8), то чтобы новый опорный план оказался невырожденным необходимо в одной из этих клеток поставить базисный ноль и считать ее занятой (табл. 2.9).
Таблица 2.9
| Потребители | Запас топлива, т |
| ||||||||||
| Хранилища |
|
|
|
|
| |||||||
|
| 5 | 4 | 3 | 6 | 0 | 70 |
| |||||
| 0 | 20 | 40 | 10 | |||||||||
|
| 4 | 3 | 5 | 1 | 0 | 90 |
| |||||
| 50 | 40 | |||||||||||
|
| 2 | 4 | 1 | 5 | 0 | 50 |
| |||||
| 50 | ||||||||||||
| Потребность в топливе, т | 50 | 70 | 40 | 40 | 10 | 210 | ||||||
|
|
|
|
|
| ||||||||
Проверим найденный план на оптимальность. Потенциалы строк и столбцов найдены непосредственно в распределительной таблице (табл. 2.9).
Найдем оценки свободных клеток:
Т.к. все оценки неотрицательны, то найденный опорный план является оптимальным, а т.к. есть нулевая оценка ( 
), то не единственен.
Итак, получен оптимальный план:
.
Транспортные издержки для этого плана:
(усл. ден. ед.).
Итак, по оптимальному плану, необходимо из хранилища А1 потребителю B2 доставить 20 т топлива, потребителю B3 – 40 т топлива; из хранилища А2 потребителю В2 доставить 50 т топлива, а потребителю В4 – 40 т топлива; из хранилища А3 доставить 50 т топлива потребителю В1.
При этом затраты на транспортировку будут минимальными и составят 490 усл. ден. ед. Нераспределенное топливо, в размере 10 т останется в хранилище А1.
Пример 2.6
В четырех хранилищах 
имеется соответственно 100, 50, 120 и 80 т картофеля. Требуется так спланировать перевозки картофеля к пяти овощным магазинам 
спрос которых равен соответственно 20, 120, 180, 30 и 100 т, чтобы суммарные транспортные издержки были минимальными. Известны стоимости перевозок 1 т картофеля (ден. ед.) из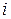 
-го ( 
) хранилища в 
-й ( 
) магазин 
.
Требуется: а) составить математическую модель задачи; б) найти оптимальный план перевозок и минимальные транспортные издержки (решить задачу методом потенциалов исходя из начального опорного плана найденного методом «северо-западного угла»).
Решение
Т.к для данной задачи выполняется условие 
, то задача является несбалансированной. Преобразуем модель к сбалансированному виду. Добавим поставщика (хранилище) 
, запас которого равен:
(20+120+180+30+100) – (100+50+120+80)=100.
Тарифы фиктивного поставщика равны нулю, т.е. 
.
Матричная модель сбалансированной задачи будет иметь вид:
| Магазины | Запас, т | ||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | ||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 | |||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 | |||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 | |||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 | |||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 | |||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | |||||
а) составить математическую модель задачи.
Введем переменные 
– количество картофеля, которое необходимо доставить из -го хранилища в 
-й магазин.
Целевая функция (затраты на перевозку всего картофеля) будет иметь вид:
Система ограничений задачи:
б) Найдем начальный опорный план методом «северо-западного угла» (табл. 2.10).
Таблица 2.10
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 20 | 80 | |||||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 40 | 10 | |||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 120 | ||||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 50 | 30 | |||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 0 | 100 | |||||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=0
=3
=–6
=5
=3
=5
=6
=6
Для проверки плана на оптимальность каждому поставщику поставим в соответствие потенциал 
, а каждому потребителю потенциал 
. Найдем их значения непосредственно в распределительной таблице. Для этого присвоим потенциалу 
и найдем значения остальных потенциалов, используя уравнения 
для занятых клеток (табл. 2.10).
Для исследования плана на оптимальность для каждой свободной клетки считаем оценки по формуле 
:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки с наименьшей отрицательной оценкой, т.к. таких клеток несколько (клетки (1,5), (2,5), (3,1), (3,4)), то возьмем любую из них, например клетку (1,5). Составим цикл пересчета относительно этой клетки (табл. 2.11).
Таблица 2.11
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 20 | 80 | – | + | |||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 40 | + | 10 | – | |||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 120 | ||||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 50 | + | 30 | – | |||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 0 | + | 100 | – | |||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение 
к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.12).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.12).
Таблица 2.12
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 20 | – | 70 | 10 | + | ||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | ||||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| + | 120 | – | ||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 60 | + | 20 | – | |||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 10 | + | 90 | – | |||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=5
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (3,1). Составим цикл пересчета относительно этой клетки (табл. 2.12). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,1) и (4,4)) нужно поставить ноль и считать ее занятой, например в клетку (1,1). Таким образом, получим новый невырожденный план перевозок (табл. 2.13).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.13).
Таблица 2.13
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 0 | – | 70 | 30 | + | ||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | ||||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | + | 100 | – | |||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 80 | ||||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| + | 30 | 70 | – | |||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=0
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (5,3). Составим цикл пересчета относительно этой клетки (табл. 2.13). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляя значение 
к поставкам в клетках, помеченных знаком «+» и вычитая из поставок в клетках, помеченных знаком «–», значения в клетках не изменятся, но в новом плане клетка (5,3) станет базисной (заполнена нулем), а клетка (1,1) станет свободной. Таким образом, получим новый невырожденный план перевозок (табл. 2.14).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.14).
Таблица 2.14
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 70 | – | 30 | + | |||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | ||||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 100 | |||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| + | 80 | – | ||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 0 | + | 30 | 70 | – | ||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (4,2). Составим цикл пересчета относительно этой клетки (табл. 2.14). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение 
к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,2) и (5,5)) нужно поставить ноль и считать ее занятой, например в клетку (5,5). Таким образом, получим новый невырожденный план перевозок (табл. 2.15).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.15).
Таблица 2.15
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 100 | ||||||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | – | + | ||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 100 | |||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 70 | + | 10 | – | |||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 70 | + | 30 | 0 | – | ||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=1
=1
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (2,5). Составим цикл пересчета относительно этой клетки (табл. 2.15). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляя значение к поставкам в клетках, помеченных знаком «+» и вычитая из поставок в клетках, помеченных знаком «–», значения в клетках не изменятся, но в новом плане клетка (2,5) станет базисной (заполнена нулем), а клетка (5,5) станет свободной. Таким образом, получим новый невырожденный план перевозок (табл. 2.16).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.16).
Таблица 2.16
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| + | 100 | – | ||||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | – | 0 | + | |||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 100 | |||||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 70 | + | 10 | – | |||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 70 | + | 30 | – | |||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=1
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (1,4). Составим цикл пересчета относительно этой клетки (табл. 2.16), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.17).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.17).
Таблица 2.17
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 10 | + | 90 | – | |||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 40 | – | 10 | + | |||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | + | 100 | – | |||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 80 | ||||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 80 | + | 20 | – | |||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=–3
=3
=2
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательные, то найденный план не оптимален. Его можно улучшить путем загрузки клетки с наименьшей отрицательной оценкой, т.к. таких две клетки ((3,2) и (3,4)), то возьмем любую из них, например клетку (3,2). Составим цикл пересчета относительно этой клетки (табл. 2.17), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.18).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.18).
Таблица 2.18
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 30 | 70 | |||||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 20 | – | + | 30 | |||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 20 | + | 80 | – | ||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 80 | ||||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 100 | ||||||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательная, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (2,3) с отрицательной оценкой. Составим цикл пересчета относительно этой клетки (табл. 2.18). Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», получим новый план перевозок (табл. 2.19).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.19).
Таблица 2.19
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 30 | – | 70 | + | |||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 20 | + | 30 | – | |||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 40 | 60 | – | + | ||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 80 | ||||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 100 | ||||||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
=0
Оценки свободных клеток:
| 
|
Так как среди оценок есть отрицательная, то найденный план не оптимален. Его можно улучшить путем загрузки клетки (3,4) с отрицательной оценкой. Составим цикл пересчета относительно этой клетки (табл. 2.19), при этом клетка (2,4), в которой звенья цикла пересекаются, не участвует в цикле. Из клеток, помеченных знаком «–» выбираем наименьшее количество груза 
. Прибавляем значение к поставкам в клетках, помеченных знаком «+» и вычитаем из поставок в клетках, помеченных знаком «–», при этом в одну из клеток, которые имеют поставки (это клетки (1,4) и (2,5)) нужно поставить ноль и считать ее занятой, например в клетку (2,5). Таким образом, получим новый невырожденный план перевозок (табл. 2.20).
Для проверки плана на оптимальность потенциалы найдем непосредственно в распределительной таблице (табл. 2.20).
Таблица 2.20
| Магазины | Запас, т | |||||||||||
| Хранилища | В1 | В2 | В3 | В4 | В5 | |||||||
| А1 | 5 | 3 | 8 | 2 | 1 | 100 |
| |||||
| 100 | ||||||||||||
| А2 | 10 | 4 | 6 | 7 | 2 | 50 |
| |||||
| 50 | 0 | |||||||||||
| А3 | 3 | 5 | 8 | 4 | 7 | 120 |
| |||||
| 20 | 40 | 30 | 30 | |||||||||
| А4 | 10 | 3 | 7 | 8 | 6 | 80 |
| |||||
| 80 | ||||||||||||
| А5 | 0 | 0 | 0 | 0 | 0 | 100 |
| |||||
| 100 | ||||||||||||
| Спрос, т | 20 | 120 | 180 | 30 | 100 | 450 | ||||||
|
|
|
|
|
| ||||||||
Оценки свободных клеток:
| 
|
Так как все оценки положительные, то найденный опорный план является оптимальным и единственным.
Итак, получили оптимальный план:
.
Транспортные издержки для этого плана:
(ден. ед.).
Итак, по оптимальному плану, необходимо из хранилища А1 магазину B5 доставить 100 т картофеля; из хранилища А2 магазину В3 доставить 50 т картофеля; из хранилища А3 доставить 20 т магазину В1, 40 т магазину В2, 30 т магазину В3 и 30 т картофеля магазину В4; из хранилища А4 доставить 80 т картофеля магазину В2; при этом спрос магазина В3 останется неудовлетворенным на 100 т картофеля. При этом затраты на транспортировку будут минимальными и составят 1260 ден. ед.
Задачи
2.1 – 2.8 Транспортная задача, представлена распределительной таблицей. Тарифы перевозок, спрос потребителей и запасы поставщиков указаны в таблице.
а) Составить математическую модель задачи;
б) Найти начальный опорный план методом «северо-западного угла», оптимальный план перевозок и соответствующие ему затраты по перевозки груза.
в) Найти начальный опорный план методом Фогеля, оптимальный план перевозок и соответствующие ему затраты по перевозки груза.
г) Найти начальный опорный план методом «минимального элемента», оптимальный план перевозок и соответствующие ему затраты по перевозки груза.
2.1
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | В4 | груза, 
|
| А1 | 4 | 5 | 7 | 1 | 40 |
| А2 | 9 | 6 | 3 | 2 | 70 |
| А3 | 6 | 5 | 2 | 4 | 60 |
| А4 | 2 | 4 | 5 | 3 | 50 |
Спрос, 
| 85 | 50 | 75 | 25 | |
2.2
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | В4 | груза,
|
| А1 | 3 | 4 | 5 | 6 | 80 |
| А2 | 9 | 6 | 3 | 7 | 70 |
| А3 | 6 | 5 | 2 | 4 | 50 |
| Спрос,
| 45 | 40 | 55 | 20 | |
2.3
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | груза, | |
| А1 | 5 | 4 | 9 | 140 | |
| А2 | 3 | 6 | 1 | 150 | |
| А3 | 4 | 8 | 6 | 130 | |
| А4 | 2 | 5 | 4 | 70 | |
| Спрос,
| 100 | 250 | 130 |
| |
2.4
| Потребители | Запасы | |||||
| Поставщики | В1 | В2 | В3 | груза, | ||
| А1 | 1 | 4 | 3 | 40 | ||
| А2 | 5 | 3 | 4 | 50 | ||
| А3 | 6 | 8 | 7 | 20 | ||
| А4 | 4 | 6 | 9 | 70 | ||
| А5 | 6 | 4 | 2 | 40 | ||
| Спрос,
| 80 | 90 | 75 |
| ||
2.5
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | В4 | груза,
|
| А1 | 5 | 3 | 4 | 6 | 20 |
| А2 | 9 | 7 | 2 | 8 | 35 |
| А3 | 2 | 4 | 1 | 5 | 15 |
| Спрос,
| 10 | 15 | 20 | 10 | |
2.6
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | В4 | груза,
|
| А1 | 7 | 5 | 6 | 1 | 50 |
| А2 | 3 | 1 | 4 | 3 | 80 |
| А3 | 6 | 7 | 9 | 8 | 40 |
| А4 | 2 | 6 | 3 | 4 | 30 |
| Спрос,
| 70 | 50 | 20 | 40 | |
2.7
| Потребители | Запасы | ||||
| Поставщики | В1 | В2 | В3 | В4 | груза,
|
| А1 | 5 | 7 | 4 | 9 | 250 |
| А2 | 3 | 1 | 6 | 5 | 350 |
| Спрос,
| 150 | 200 | 100 | 250 | |
2.8
| Потребители | Запасы | |||||
| Поставщики | В1 | В2 | В3 | В4 | В5 | груза,
|
| А1 | 3 | 6 | 7 | 2 | 9 | 60 |
| А2 | 5 | 2 | 5 | 4 | 8 | 30 |
| А3 | 8 | 4 | 3 | 5 | 2 | 90 |
| Спрос,
| 20 | 40 | 30 | 10 | 15 | |
2.9
Четыре магазина 
получают овощи из трех совхозов 
которые ежедневно могут поставлять соответственно 15, 16 и 24 т. Суточные потребности магазинов составляют 12, 14, 16 и 15 т. Известна матрица транспортных расходов на доставку 1 т овощей из совхоза магазину:
.
Найти оптимальный план доставки овощей из совхозов магазинам и минимальные транспортные издержки на перевозку всех овощей.
2.10
На пять строительных площадок 
поступает кирпич с трех заводов. Ежедневная потребность в кирпиче на строительных площадках равна соответственно: 50, 65, 45, 40 и 60 тыс. шт. Данные о производительности заводов за день и транспортные расходы на 1 тыс. шт. приведены в таблице:
| Транспортные расходы на 1 тыс. шт. по строительным площадкам, ден. ед. | Производитель-ность заводов за день, тыс. шт. | |||||
| Заводы | В1 | В2 | В3 | В4 | В5 | |
| А1 | 5 | 3 | 4 | 2 | 5 | 90 |
| А2 | 9 | 6 | 7 | 5 | 3 | 110 |
| А3 | 2 | 4 | 8 | 1 | 4 | 80 |
Определить оптимальный план закрепления строительных площадок за кирпичными заводами, чтобы затраты на транспортировку кирпича были минимальными.
2.11
На заводах №1, №2 и №3 производится однородная продукция в количестве 70, 80 и 60 единиц. При этом затраты на производство единицы продукции на заводах составляют соответственно 3, 2 и 4 ден.ед. Четырем потребителям требуется соответственно 40, 65, 55 и 60 единиц продукции. Расходы 
(ден. ед.) по перевозке единицы продукции с 
-го завода 
-му потребителю известны.
.
Для полного удовлетворения потребностей необходимо увеличить выпуск продукции на первом заводе. При этом дополнительные затраты на производство единицы дополнительной продукции равны 1 ден.ед.
Требуется найти оптимальный план доставки продукции потребителю, при котором совокупные затраты, связанные с изготовлением продукции и ее доставкой потребителям будут минимальными.
2.12
Составить план посева зерновых культур (с учетом плодородия почвы), при котором урожай будет максимальным. Площадь I участка равна 200 га, участка II – 150 га, участка III – 250 га, участка IV – 100 га. Все необходимые данные приведены в таблице:
| Зерновые культуры | Урожайность по участкам, ц/га | Посевные | |||
| I | II | III | IV | площади, га | |
| Рожь | 30 | 25 | 28 | 26 | 180 |
| Пшеница | 40 | 37 | 35 | 38 | 350 |
| Ячмень | 35 | 32 | 29 | 34 | 170 |
Глава 3. Динамическое программирование
Динамическое программирование (ДП) – это метод нахождения оптимальных решений в задачах с многошаговой (многоэтапной) структурой.
Приведем общую постановку задачи ДП. Рассматривается управляемый процесс (распределение средств между предприятиями, использование ресурсов в течение ряда лет и т.п.). В результате управления система (объект управления) переводится из начального состояния 
в состояние 
. Предположим, что управление можно разбить на 
шагов. На каждом шаге выбирается одно из множества допустимых управлений 
, переводящее систему в одно из состояний множества 
. Элементы множества 
и определяются из условий конкретной задачи. Последовательность состояний системы можно изобразить в виде графа состояний, представленного на рис. 3.1.
Рис. 3.1
На каждом шаге n достигается эффект 
. Предположим, что общий эффект является суммой эффектов, достигнутых на каждом шаге. Тогда задача ДП формулируется так: определить такое допустимое управление 
, переводящее систему из состояния 
в состояние 
, при котором функция цели 
принимает наибольшее (наименьшее) значение, т.е.
Решение задач методом ДП осуществляется на основе принципа оптимальности, который был сформулирован американским ученым Р.Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Обозначим через 
условно-оптимальное значение целевой функции на интервале от шага n до последнего -го шага включительно, при условии, что перед n-ым шагом система находилась в одном из состояний множества 
, а на n-ом шаге было выбрано такое управление из множества , которое обеспечило целевой функции условно-оптимальное значение, тогда 
условно-оптимальное значение целевой функции в интервале от (n +1)-го до -го шага включительно.
В принятых обозначениях принцип оптимальности Беллмана можно записать в математической форме следующим образом
. (3.1)
Равенство (3.1) называется основным функциональным уравнением динамического программирования. Для каждой конкретной задачи уравнение имеет особый вид.
Вычислительная процедура метода ДП распадается на два этапа: условную и безусловную оптимизацию.
На этапе условной оптимизации в соответствии с функциональным уравнением определяются оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.
На этапе безусловной оптимизации шаги рассматриваются, начиная с первого. Поскольку исходное состояние известно, выбирается оптимальное управление из множества 
. Выбранное оптимальное управление 
приводит систему во вполне определенное состояние 
. Благодаря тому, что исходное состояние 
в начале второго шага известно, становится возможным выбрать оптимальное управление на втором шаге и т.д. Таким образом, строится цепь взаимосвязанных решений безусловной оптимизации.
3.1. Задача оптимального распределения ресурсов
Пусть на реконструкцию и модернизацию основного производства объединению выделяется некоторый объем материальных ресурсов Х. Имеется N предприятий, между которыми нужно распределить данный ресурс. Обозначим через 
прибыль, которому приносит народному хозяйству выделение j-му предприятию 
единиц ресурса. Предполагается, что размер прибыли зависит как от выделенного количества ресурса, так и от предприятия. Причем прибыль, получаемая предприятиями измеряется в одних и тех же единицах и общая прибыль объединения состоит из прибылей отдельных предприятий. Необходимо найти оптимальный план распределения ресурсов между предприятиями, при котором общая прибыль объединения будет максимальной.
Поставленную задачу нужно рассмотреть как многошаговую.
На этапе условной оптимизации будем рассматривать эффективность вложения средств на одном (например, на первом предприятии), на двух предприятиях вместе (на первом и втором), на трех предприятиях вместе (на первом, втором и третьем) и т.д., и наконец, на всех N предприятиях вместе. Задача состоит в определении наибольшего значения функции 
при условии, что 
.
Воспользуемся рекуррентным соотношением Беллмана (3.1), которое для данной задачи приводит к следующим функциональным уравнениям при 
:
Здесь функция 
определяет максимальную прибыль первого предприятия при выделении ему x единиц ресурса, функция 
определяет максимальную прибыль первого и второго предприятий вместе при выделении им x единиц ресурса, функция 
определяет максимальную прибыль первого, второго и третьего предприятий вместе при выделении им x единиц ресурса и т.д., и наконец, функция 
определяет максимальную прибыль всех предприятий вместе при выделении им x единиц ресурса.
На этапе безусловной оптимизации определяется оптимальный план распределения ресурсов между предприятиями.
Пример 3.1.
Для увеличения объемов выпуска пользующейся повышенным спросом продукции четырем предприятиям производственного объединения выделены средства в размере 50 млн. руб. Каждому из предприятий может быть выделено: 0, 10, 20, 30, 40 или 50 млн. руб. При этом ежегодный прирост выпуска продукции каждым из предприятий в зависимости от капиталовложений известен и приведен в табл. 3.1.
Таблица 3.1
| Объем выделенных средств x (млн. руб.) | Ежегодный прирост выпуска продукции (млн. руб.), в зависимости от объема выделенных средств | |||
| 
| 
|
| |
| 0 | 0 | 0 | 0 | 0 |
| 10 | 3 | 5 | 2 | 4 |
| 20 | 6 | 8 | 5 | 7 |
| 30 | 9 | 12 | 11 | 10 |
| 40 | 14 | 15 | 14 | 13 |
| 50 | 17 | 18 | 18 | 17 |
Найти оптимальный план распределения средств между предприятиями, обеспечивающий максимальный ежегодный прирост выпуска продукции производственным объединением.
Решение
I этап. Условная оптимизация.
1-й шаг. Находим максимальный ежегодный прирост выпуска продукции первого предприятия при выделении ему x млн. руб. по формуле (3.2), которая эквивалентна формуле 
. Значения функции и условно-оптимальные значения объема выделенных средств первому предприятию 
запишем в табл. 3.2.
Таблица 3.2
| x |
| 
|
| 0 | 0 | 0 |
| 10 | 3 | 10 |
| 20 | 6 | 20 |
| 30 | 9 | 30 |
| 40 | 14 | 40 |
| 50 | 17 | 50 |
2-й шаг. Находим максимальный ежегодный прирост выпуска продукции первого и второго предприятий вместе 
при выделении им x млн. руб. по формуле (3.3), т.е. 
Вычисление функции произведем в таблице (табл. 3.3), последние два столбца которой – это значения функции и условно-оптимальные значения объема выделенных средств второму предприятию .
Таблица 3.3
|
x |
|
|
| |||||
| 0 | 10 | 20 | 30 | 40 | 50 | |||
| 10 | 0+3 | 5+0 | – | – | – | – | 5 | 10 |
| 20 | 0+6 | 5+3 | 8+0 | – | – | – | 8 | 10, 20 |
| 30 | 0+9 | 5+6 | 8+3 | 12+0 | – | – | 12 | 30 |
| 40 | 0+14 | 5+9 | 8+6 | 12+3 | 15+0 | – | 15 | 30, 40 |
| 50 | 0+17 | 5+14 | 8+9 | 12+6 | 15+3 | 18+0 | 19 | 10 |
3-й шаг. Находим максимальный ежегодный прирост выпуска продукции первого, второго и третьего предприятий вместе 
при выделении им x млн. руб. по формуле (3.3), т.е. 
Вычисление функции произведем в таблице (табл. 3.4), последние два столбца которой – это значения функции и условно-оптимальные значения объема выделенных средств третьему предприятию 
.
Таблица 3.4
|
x |
|
|
| |||||
| 0 | 10 | 20 | 30 | 40 | 50 | |||
| 10 | 0+5 | 2+0 | – | – | – | – | 5 | 0 |
| 20 | 0+8 | 2+5 | 5+0 | – | – | – | 8 | 0 |
| 30 | 0+12 | 2+8 | 5+5 | 11+0 | – | – | 12 | 0 |
| 40 | 0+15 | 2+12 | 5+8 | 11+5 | 14+0 | – | 16 | 30 |
| 50 | 0+19 | 2+15 | 5+12 | 11+8 | 14+5 | 18+0 | 19 | 0, 30, 40 |
4-й шаг. Находим максимальный ежегодный прирост выпуска продукции четырех предприятий вместе 
при выделении им x млн. руб. по формуле (3.3), т.е. 
Т.к. это последний шаг условной оптимизации и значения функции в дальнейших вычислениях не будут использоваться, то достаточно вычислить значение функции при x=50 (т.е. максимальный ежегодный прирост выпуска продукции четырех предприятий при выделении им 50 млн. руб.). Вычисление функции произведем в таблице (табл. 3.5), последние два столбца которой – это значение функции 
и условно-оптимальное значение объема выделенных средств четвертому предприятию .
Таблица 3.5
|
x |
|
|
| |||||
| 0 | 10 | 20 | 30 | 40 | 50 | |||
| 50 | 0+19 | 4+16 | 7+12 | 10+8 | 13+5 | 17+0 | 20 | 10 |
Итак, максимальный ежегодный прирост выпуска продукции четырех предприятий при выделении им 50 млн. руб. будет 
млн. руб., при этом четвертому предприятию нужно выделить 
млн. руб.
II этап. Безусловная оптимизация.
Найдем оптимальный план распределения денежных средств между предприятиями.
1-й шаг. Итак, максимальный прирост выпуска продукции составит 20 млн. руб., при этом четвертому предприятию нужно выделить млн. руб. (табл. 3.5).
2-й шаг. Тогда определим сумму, которая достанется первым трем предприятиям: 
млн. руб. По табл. 3.4 находим, что максимальный прирост выпуска продукции первых трех предприятий при выделении им 40 млн. руб. 
будет при 
, следовательно, третьему предприятию нужно выделить 
млн. руб.
3-й шаг. Теперь определим сумму, которая достанется первым двум предприятиям: 
млн. руб. По табл. 3.3 находим, что максимальный прирост выпуска продукции первых двух предприятий при выделении им 10 млн. руб. 
будет при 
, следовательно, второму предприятию нужно выделить 
млн. руб.
4-й шаг. Теперь определим сумму, которая достанется первому предприятию: 
млн. руб., следовательно, первому предприятию дополнительные средства выделять не целесообразно.
Итак, оптимальный план распределения капиталовложений между предприятиями 
обеспечит максимальное увеличение выпуска продукции, в размере млн. руб. или, в качестве проверки,
=20 (млн. руб.)
Задачи
3.1.1 – 3.1.6 Производственному объединению, состоящему из нескольких предприятий, выделены дополнительные средства в размере 400 тыс. руб. Прибыль каждого предприятия зависит от объема выделенных дополнительных средств и приведена в таблице. Распределить дополнительные средства между предприятиями так, чтобы их совокупная прибыль была максимальной.
3.1.1
| Выделенные дополнительные средства, тыс. руб. | Предприятие | |||
| №1 | №2 | №3 | №4 | |
| Прибыль, тыс. руб. | ||||
| 80 | 7 | 9 | 8 | 7 |
| 160 | 13 | 16 | 14 | 15 |
| 240 | 21 | 23 | 22 | 21 |
| 320 | 27 | 27 | 28 | 29 |
| 400 | 34 | 35 | 36 | 35 |
3.1.2
| Выделенные дополнительные средства, тыс. руб. | Предприятие | |||
| №1 | №2 | №3 | №4 | |
| Прибыль, тыс. руб. | ||||
| 50 | 6 | 7 | 8 | 7 |
| 100 | 13 | 12 | 14 | 13 |
| 150 | 17 | 16 | 18 | 16 |
| 200 | 23 | 22 | 23 | 24 |
| 250 | 30 | 31 | 30 | 31 |
| 300 | 37 | 36 | 37 | 35 |
| 350 | 42 | 41 | 41 | 40 |
| 400 | 47 | 46 | 48 | 45 |
3.1.3
| Выделенные дополнительные средства, тыс. руб. | Предприятие | ||||
| №1 | №2 | №3 | №4 | №5 | |
| Прибыль, тыс. руб. | |||||
| 100 | 10 | 9 | 11 | 8 | 10 |
| 200 | 19 | 17 | 20 | 21 | 20 |
| 300 | 31 | 30 | 28 | 29 | 31 |
| 400 | 38 | 39 | 37 | 38 | 37 |
3.1.4
| Выделенные дополнительные средства, тыс. руб. | Предприятие | ||||
| №1 | №2 | №3 | №4 | №5 | |
| Прибыль, тыс. руб. | |||||
| 80 | 5 | 6 | 4 | 5 | 6 |
| 160 | 11 | 10 | 9 | 10 | 9 |
| 240 | 14 | 15 | 16 | 15 | 14 |
| 320 | 21 | 20 | 20 | 21 | 19 |
| 400 | 25 | 24 | 23 | 24 | 23 |
3.1.5
| Выделенные дополнительные средства, тыс. руб. | Предприятие | ||
| №1 | №2 | №3 | |
| Прибыль, тыс. руб. | |||
| 50 | 6 | 7 | 5 |
| 100 | 13 | 12 | 11 |
| 150 | 17 | 16 | 15 |
| 200 | 23 | 22 | 22 |
| 250 | 30 | 31 | 29 |
| 300 | 37 | 36 | 35 |
| 350 | 42 | 41 | 40 |
| 400 | 47 | 46 | 45 |
3.1.6
| Выделенные дополнительные средства, тыс. руб. | Предприятие | |||||
| №1 | №2 | №3 | №4 | №5 | №6 | |
| Прибыль, тыс. руб. | ||||||
| 100 | 10 | 9 | 11 | 8 | 10 | 9 |
| 200 | 19 | 17 | 20 | 21 | 20 | 18 |
| 300 | 31 | 30 | 28 | 29 | 31 | 29 |
| 400 | 38 | 39 | 37 | 38 | 37 | 39 |
3.1.7 Самолет загружается предметами П1, П2 и П3. Предмет П i имеет массу mi (весовых единиц) и стоимость ri (денежных единиц) ( 
). Грузоподъемность самолета равна M. Необходимые числовые данные приведены в таблице. Установить, сколько предметов каждого типа следует поместить в самолет, чтобы общая стоимость груза была максимальной. Задачу решить для следующих вариантов грузоподъемности самолета:
а) M=5; б) M=6; в) M=7; г) M=8; д) M=9; е) M=10.
| П i | mi | ri |
| П1 | 1 | 14 |
| П2 | 2 | 30 |
| П3 | 3 | 40 |
3.1.8 Вагон загружается предметами П1, П2, П3 и П4. Предмет П i имеет массу mi (весовых единиц) и стоимость ri (денежных единиц) ( 
). Грузоподъемность вагона равна M. Необходимые числовые данные приведены в таблице. Установить, сколько предметов каждого типа следует поместить в вагон, чтобы общая стоимость груза была максимальной. Задачу решить для следующих вариантов грузоподъемности вагона:
а) M=5; б) M=6; в) M=7; г) M=8; д) M=9; е) M=10.
| П i | mi | ri |
| П1 | 1 | 2 |
| П2 | 2 | 5 |
| П3 | 3 | 7 |
| П4 | 5 | 13 |
3.2. Задача об оптимальной стратегии замены оборудования
Известно, что оборудование со временем изнашивается, стареет физически и морально. В процессе эксплуатации падает производительность, и растут эксплуатационные расходы на текущий ремонт. Со временем возникает необходимость замены оборудования, так как его дальнейшая эксплуатация обходится дороже, чем замена. Отсюда задача о замене оборудования может быть сформулирована следующим образом.
Разработать оптимальную стратегию замены оборудования возраста 
лет в плановом периоде продолжительностью лет, если известны:
– стоимость продукции, производимой в течение года на оборудовании возраста 
лет ( 
);
– ежегодные расходы, связанные с эксплуатацией оборудования возраста лет ( );
– остаточная стоимость оборудования возраста лет;
– стоимость нового оборудования и расходы, связанные с его установкой, наладкой и запуском.
Поставленную задачу нужно рассмотреть как многошаговую.
На этапе условной оптимизации будем находить максимальную прибыль за последний год планового периода эксплуатации оборудования возраста t лет, за два последних года, за три последних года и т.д., и наконец, за весь плановый период.
В начале каждого года имеется две возможности – сохранить оборудование и получить прибыль 
или заменить его и получить прибыль 
. Прибыль от использования оборудования в последнем -м году планового периода запишется в следующем виде
(3.4)
а прибыль от использования оборудования в период с 
-го по -й год
(3.5)
где 
– прибыль от использования оборудования в период с 
-го по -й год.
В случае, если оба управления («сохранение» и «замена») приводят к одной и той же прибыли, то целесообразно выбрать управление «сохранение».
На этапе безусловной оптимизации определяется оптимальная стратегия замены оборудования на протяжении всего планового периода.
Пример 3.2
Найти оптимальную стратегию замены оборудования возраста 3 года на период продолжительностью 10 лет, если для каждого года планового периода известны стоимость продукции, производимой с использованием этого оборудования, и эксплуатационные расходы (табл. 3.6). Известны также остаточная стоимость, не зависящая от возраста оборудования и составляющая 4 ден. ед., и стоимость нового оборудования, равная 18 ден. ед., не меняющаяся в плановом периоде.
Таблица 3.6
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 31 | 30 | 28 | 28 | 27 | 26 | 26 | 25 | 24 | 24 | 23 |
|
| 8 | 9 | 9 | 10 | 10 | 10 | 11 | 12 | 14 | 16 | 18 |
Решение
I этап. Условная оптимизация.
1-й шаг. 
. Начнем процедуру условной оптимизации с последнего, десятого года планового периода. Найдем максимальную прибыль, получаемую от оборудования возраста t ( 
) лет за последний год планового периода 
. Функциональное уравнение (3.4) с учетом числовых данных примера принимает вид
.
Тогда
;
;
;
;
;
;
;
;
;
;
.
Полученные результаты занесём в таблицу (первая строка табл. 3.7).
2-й шаг. 
. Найдем максимальную прибыль, получаемую от оборудования возраста t ( ) лет за последние два года (9-ый и 10-ый) планового периода 
. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид
.
Тогда
;
;
;
;
;
;
.
Т.к. оборудование возраста 6 лет следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать 
.
Полученные результаты занесём в таблицу (вторая строка табл. 3.7).
3-й шаг. 
. Найдем максимальную прибыль, получаемую от оборудования возраста t ( ) лет за последние три года (с 8-го по 10-ый) планового периода 
. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид
.
Тогда
;
;
;
;
;
Т.к. оборудование возраста 4 года следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать 
.
Полученные результаты занесём в таблицу (третья строка табл. 3.7).
4-й шаг. 
. Найдем максимальную прибыль, получаемую от оборудования возраста t ( ) лет за последние четыре года (с 7-го по 10-ый) планового периода 
. Функциональное уравнение (3.5) с учетом числовых данных примера принимает вид
.
Тогда
;
;
;
.
Здесь оба управления («сохранение» и «замена») приводят к одной и той же прибыли, то целесообразно выбрать управление «сохранение».
;
Т.к. оборудование возраста 4 года следует заменить, то и на более старом оборудовании работать будет не целесообразно, т.е. можно сразу записать 
.
Полученные результаты занесём в таблицу (четвертая строка табл. 3.7).
Продолжая вычисления описанным способом, постепенно заполняем всю таблицу (табл. 3.7). При этом области «сохранения» и «замены» разделим жирной линией (табл. 3.7).
Таблица 3.7
|
|
| ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 23 | 21 | 19 | 18 | 17 | 16 | 15 | 13 | 10 | 9 | 9 |
| 44 | 40 | 37 | 35 | 33 | 31 | 30 | 30 | 30 | 30 | 30 |
| 63 | 58 | 54 | 51 | 49 | 49 | 49 | 49 | 49 | 49 | 49 |
| 81 | 75 | 70 | 67 | 67 | 67 | 67 | 67 | 67 | 67 | 67 |
| 98 | 91 | 86 | 85 | 84 | 84 | 84 | 84 | 84 | 84 | 84 |
| 114 | 107 | 104 | 102 | 101 | 100 | 100 | 100 | 100 | 100 | 100 |
| 130 | 125 | 121 | 119 | 117 | 116 | 116 | 116 | 116 | 116 | 116 |
| 148 | 142 | 138 | 135 | 134 | 134 | 134 | 134 | 134 | 134 | 134 |
| 165 | 159 | 154 | 152 | 151 | 151 | 151 | 151 | 151 | 151 | 151 |
| 182 | 175 | 171 | 169 | 168 | 168 | 168 | 168 | 168 | 168 | 168 |
Итак, максимальную прибыль, получаемую от оборудования возраста 3 года за весь плановый период 
ден. ед.
II этап. Безусловная оптимизация.
Найдем теперь оптимальную политику, обеспечивающую эту прибыль. Значение 169 записано слева от жирной линии в области «сохранения». Это означает, что в начале первого года принимается решение о сохранении оборудования. К началу второго года возраст оборудования будет 3+1=4 года. Т.к. 
находится слева от жирной линии, то и второй год нужно работать на имеющемся оборудовании. Тогда к началу третьего года возраст оборудования будет 4+1=5 лет. Т.к. 
находится справа от жирной линии, в области «замены», то в начале третьего года следует заменить оборудование и третий год работать на новом оборудовании. Тогда к началу четвертого года возраст оборудования составит один год. Т.к. 
находится слева от жирной линии, то четвертый год следует работать на имеющемся оборудовании. Продолжая рассуждать таким образом, последовательно находим 
– «сохранение», 
– «сохранение», 
– «замена», 
– «сохранение», 
– «сохранение», 
– «сохранение». Эти значения для наглядности выделены в табл. 3.7 жирным шрифтом.
Цепь решений безусловной оптимизации можно изобразить символически следующим образом.
.
Итак, на оборудовании возраста 3 года следует работать 2 года, затем произвести замену оборудования, на новом оборудовании работать 3-й, 4-й, 5-й и 6-й годы, после чего произвести замену оборудования и на следующем оборудовании работать 7-й, 8-й, 9-й и 10-й годы планового периода. При этом прибыль будет максимальной и составит 
=169 ден. ед.
Задачи
3.2.1
Найти оптимальную стратегию замены оборудования возраста k лет на период продолжительностью 6 лет. Для каждого года планового периода известны стоимость продукции, производимой с использованием этого оборудования и эксплуатационные расходы . Необходимые числовые данные приведены в таблице. Известны также остаточная стоимость, не зависящая от возраста оборудования и составляющая s ден. ед., и стоимость нового оборудования, равная p ден. ед., не меняющаяся в плановом периоде. Задачу решить для следующих вариантов значений k, s, и p:
а) k=2, s=12, p=32; б) k=0, s=8, p=27; в) k=5, s=11, p=29;
г) k=1, s=9, p=28; д) k=3, s=10, p=27; е) k=4, s=13, p=31.
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| 30 | 29 | 28 | 26 | 25 | 23 | 22 |
|
| 10 | 11 | 11 | 12 | 13 | 13 | 14 |
3.2.2
Найти оптимальную стратегию замены оборудования возраста k лет на период продолжительностью 5 лет. Для каждого года планового периода известны стоимость продукции, производимой с использованием этого оборудования, эксплуатационные расходы и остаточная стоимость оборудования возраста t лет 
. Необходимые числовые данные приведены в таблице. Известна также стоимость нового оборудования, равная p ден. ед., не меняющаяся в плановом периоде. Задачу решить для следующих вариантов значений k и p:
а) k=2, p=45; б) k=0, p=42; в) k=5, p=43; г) k=1, p=41; д) k=3, p=44.
|
| 0 | 1 | 2 | 3 | 4 | 5 |
|
| 25 | 24 | 23 | 23 | 22 | 20 |
|
| 10 | 11 | 11 | 12 | 13 | 14 |
|
| 40 | 38 | 37 | 35 | 33 | 31 |
Дата добавления: 2018-09-20; просмотров: 939; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!