Основные теоремы об упругих системах
Любое сооружение под воздействием внешних факторов, таких как внешняя нагрузка, тепловое воздействие или кинематическое смещение опор, деформируется, изменяя свою первоначальную форму и принимая новую форму равновесия, когда влияние внешних воздействий компенсируется появляющимися в процессе деформирования внутренними реактивными усилиями. Основная задача строительной механики в этом случае – в определении этих усилий. Причем для статически определимых систем такая задача решается полностью при помощи одних лишь уравнений статики.
Расчет же статически неопределимых систем (в частности при использовании метода сил) должен быть дополнен условиями, носящими кинематический характер и связанными с определением перемещений сооружения вследствие его деформаций под нагрузкой.
Кроме того, умение определять перемещения необходимо при оценке жесткости сооружения и его отдельных элементов, при оценке его устойчивости и во многих других случаях.
Всё это говорит в пользу того, что разработка общих методов определения перемещений строительных конструкций – одна из важнейших задач строительной механики. Для этого используем гипотезы физического характера, относящиеся к работе как самого сооружения, так и того материала, из которого оно создано. Это гипотезы, лежащие в основе классической строительной механики: идеальная упругость материала и системы в целом, линейная зависимость между нагрузкой и вызываемыми ей перемещениями, малость перемещений упругой системы относительно её наименьшего размера, запрет на превышение величины действующих напряжений предела пропорциональности, выполнение принципа независимости действия сил.
|
|
|
Сочетание всего вышеперечисленного приводит к понятию линейно-деформируемой системы, которую можно описать следующей зависимостью:
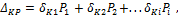
где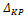 
- перемещение определенного типа в т. К от системы сил;
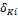- перемещение того же типа в т. К от силы 
.
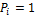Это обобщенный закон Гука, а системы, для которых он справедлив, называют линейно-деформируемыми. На рис.4.1 отображена зависимость величины перемещений в зависимости от приложенной нагрузки.
| P |
| Рис.4.1 |
| Δ |
Основой для разработки метода определения перемещений упругих систем служат общие законы деформирования, носящие название общих теорем о деформируемых системах. Они, в свою очередь, являются частными случаями общих закономерностей, носящих название «начал» или «принципов», имеющих под собой энергетическую базу. Ниже мы остановимся на изучении энергетических свойств упругих систем, рассмотрев вопросы, затрагивающие определение работы внешних и внутренних сил и потенциальной энергии деформаций.
|
|
|
Работа внешних сил.
Для подготовки к рассмотрению данного вопроса сделаем следующее.
а) Введем понятие обобщенной силы и обобщенного перемещения, которые позволят проводить все дальнейшие выкладки в общей и лаконичной форме. Итак, обобщенная сила. Под этим понятием кроется любое силовое воздействие (сосредоточенная сила, группа таких сил, распределенная нагрузка, сосредоточенный момент). В то же время обобщенное перемещение – это тот вид перемещения, на котором обобщенная сила производит работу. Для сосредоточенной силы –это линейное перемещение, для сосредоточенного момента – это угол поворота, а для распределенной нагрузки – это площадь эпюры перемещений, расположенная в границах действия такой нагрузки.
б) Действительная и возможная работа сил.
Назовем работу действительной, если её совершают данные силы на перемещениях, созданных самими этими силами. Назовем работу возможной, если её совершили данные силы на перемещениях, созданных какими-либо посторонними воздействиями. В качестве примера рассмотрим следующую ситуацию (рис.4.2): вначале к балке прикладывают сосредоточенную силу 
, в результате чего балка в месте её приложения получает перемещение 
. Затем к балке прикладывают силу 
, в результате чего в месте приложения первой силы появляется дополнительное перемещение по направлению её действия 
.
|
|
|
в) При медленном и постоянном возрастании внешней нагрузки и вызванных ею перемещениях ускорения, возникающие при деформировании системы пренебрежительно малы, и не учитываются в расчетах. Подобный вид приложения нагрузки называют статическим.
Итак, вернемся к вопросу вычисления действительной работы внешних сил. Рассмотрим следующую ситуацию:
- сосредоточенная сила Р приложена к системе, материал которой удовлетворяет закону Гука;
- при малых деформациях применим принцип независимости действия сил;
- будем считать, что перемещения отдельных точек системы прямо пропорциональны величине вызвавших их нагрузок:
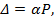
некий коэффициент, учитывающий свойства материала, схему и размеры системы.
Увеличив приложенную нагрузку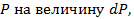 
вызовем прирост перемещения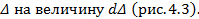 
| Δ dΔ |
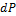P
|
|
|
|
Рис. 4.3
Элементарную работу внешней силы P на перемещении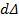 
запишем таким образом:
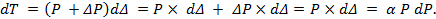
Работа, совершенная статически приложенной внешней силой P, равна:
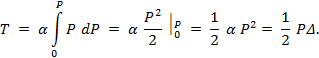
ТЕОРЕМА КЛАЙПЕРОНА. (жившего в первой половине 19 века французского физика и инженера, получившего, к примеру, уравнение состояния идеального газа Менделеева-Клапейрона ).
Действительная работа внешней статически приложенной силы равна половине произведения её конечного значения на окончательную величину вызванного ей перемещения.
Возможная работа внешней силы определяется произведением её конечного значения на весь пройденный ею путь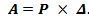 
| M |
| φ |
Рис. 4.4
При действии сосредоточенного момента М его действительная работа вычисляется следующим образом (рис. 4.4)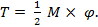 
Работа внутренних сил.
В процессе нагружения упругой системы работу совершают не только внешние, но и развивающиеся во всех деформируемых элементах внутренние силы. Поскольку в упругой системе не происходит потерь энергии на преодоление трения, вследствие выделения тепла и пр., действительная работа внешних сил T равна и противоположна по знаку работе сил внутренних W, что является следствием закона сохранения энергии:
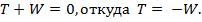
Чтобы получить выражение для работы внутренних сил W, рассмотрим произвольную систему под действием внешней нагрузки (рис.4.5, а). Выделим двумя сечениями бесконечно малый элемент, длиной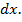 
|
|
|
|
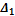
| a |
| б |
| M |
| M |
| N |
| N |
| Q |
| Q |
| dx |
| h |
Рис. 4.5
Приложим усилия M, Q и N, действующие на отсеченный элемент со стороны отброшенных частей рамы, и рассмотрим вызванные этими усилиями деформации. Отметим, что при такой постановке вопроса работа внутренних усилий W может быть вычислена, как интегральная сумма работ, совершенная статически возрастающими усилиями M, Q и N на соответствующих деформациях элемента dx. Элементарная действительная работа внутренних усилий равна:
Рассмотрим независимое действие каждого из внутренних усилий на отсеченный элемент.
| M |
| M |
| dx |
| Рис. 4.6 |
| φ |
Действие моментов М приводит к изменению формы элемента (рис.4.6), а угол φ вычисляется по известной из сопромата формуле:
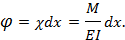
Элементарная работа моментов М на угловом перемещении φ может быть вычислена таким образом:
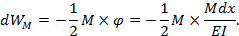
Наличие знака “минус» в вышеприведенном выражении указывает на то, что направление внутренних усилий М самого элемента dx противоположно направлению его деформаций. Отсюда можно сделать важный вывод: работа внутренних усилий при загружении упругого тела всегда положительна.
Действие продольных сил N также приводит к изменению формы элемента (рис.4,7), в данном случае к его удлинению или укорочению, а деформация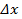 
в соответствии с законом Гука вычисляется по формуле:
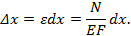
Элементарная работа продольных сил N на перемещении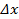 
может быть вычислена так:
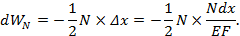
Действие поперечных сил Q приводит к изменению формы элемента (рис.4.8) – сдвигу сечений на некоторую величину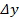 
, появлению угла γ. Нетрудно заметить, что 
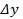связан с углом γ таким образом:
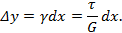
| Q |
| Q |
| dx |
| Рис. 4.8 |
| γ |
| γ |
|
По теореме Журавского
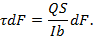
При этом элементарная работа бесконечно малой касательной силы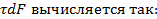 
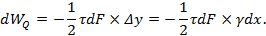
Работа всех касательных сил, распределенных по площади поперечного сечения F, может быть получена следующим образом:
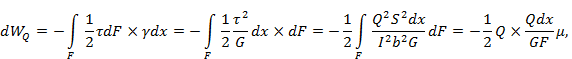
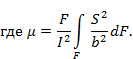
Коэффициент μ отражает зависимость величины вычисляемой элементарной работы от формы поперечного сечения элемента. Так, для прямоугольного сечения μ=1,2, для круга – 1,18, для двутавра –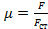 
, где F – площадь всего поперечного сечения, а 
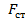- площадь поперечного сечения стенки двутавра.
Таким образом, полная элементарная работа при одновременном действии всех внутренних усилий предстает в таком виде:
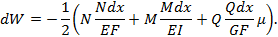
Следует обратить внимание на то, что вышеперечисленные внутренние усилия совершают работу только на своих - «собственных» - перемещениях, в то время как их возможная работа на перемещениях, созданных другими внутренними усилиями, равна нулю.
Просуммировав элементарную работу вначале по отдельным стержням системы, а затем и по всем её стержням, получим выражение для работы внутренних сил:
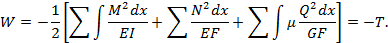
При смене знака выражение для работы внутренних сил можно использовать и для вычисления действительной работы сил внешних
Теорема о взаимности работ.
Рассмотрим два состояния упругой системы, находящейся в равновесии (рис.4.9). Обозначим некоторое перемещение системы через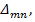 
где m
| P2 |
| 1 |
| 2 |
| * |
| * |
| k |
|
|
| Рис.4.9 |
| P1 |
| j |
| * |
| 2 |
| * |
| 1 |
|
|
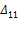
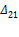
определяет направление перемещения, а n –причину его вызвавшую. Таким образом,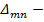 
это перемещение по направлению действия обобщенной силы m,вызванное действием обобщенной силы n.
Перемещение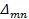 
может предстать либо в виде линейного смещения, либо в виде угла поворота в зависимости от того, является ли обобщенная сила сосредоточенной нагрузкой, либо сосредоточенным моментом. Под обобщенной силой «n» понимается любая нагрузка, вызвавшая данное перемещение.
В соответствии с вышеизложенным,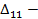 
это перемещение по направлению силы Р1 вызванное самой силой Р1, 
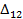- перемещение по направлению силы Р1, вызванное силой Р2, и т.п.
Обозначим действительную работу силы первого состояния - Р1 -на её же перемещениях через А11, а действительную работу силы второго состояния – Р2 – на своих перемещениях через А22.
Тогда,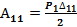 
и 
.
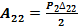Рассмотрим два состояния упругой системы. В первом случае вначале приложим силу Р1, а затем – силу Р2. На рис.4.10 – первое состояние упругой системы.
| P1 |
| ① |
|
|
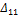
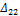
| P2 |
|
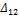
| Рис.4.10 |
Обозначим возможную работу силы Р1 на перемещении, вызванном силой Р2 через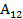 
. В результате, суммарная работа сил Р1 и Р2 становится равной:
+ 
.
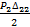Во втором случае первоначально приложим силу Р2, а затем только – силу Р1. На рис.4.11 изображено созданное второе состояние системы.
P1
②
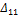
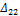
P2
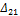
Рис.4.11
Обозначим через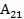 
возможную работу силы Р2 на перемещении, вызванном силой Р1. В результате, суммарная работа сил Р1 и Р2 становится равной:
+ .
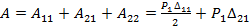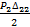Сравнив правые части выражений для работы А первого и второго состояния приходим к выводу, что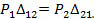 
Отсюда следует, что:
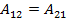
ТЕОРЕМА БЭТТИ. Работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.
Преобразуем выражение для работы в первом состоянии упругой системы, выразив её через работу внутренних сил:
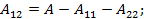
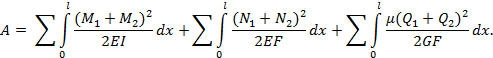
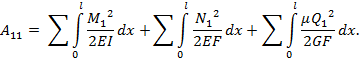
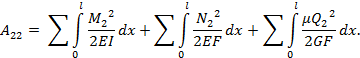
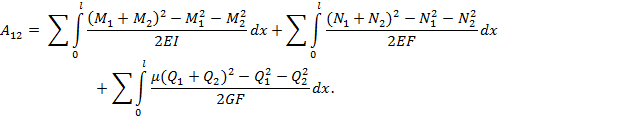
Преобразовав полученное выражение, получим:
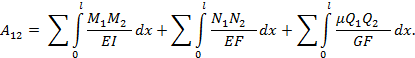
Теорема о взаимности перемещений.
Рассмотрим два состояния упругой системы (рис.4.12). Сначала приложим в точке 1 сосредоточенную силу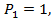 
зафиксировав в точке 2 перемещение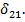 
Затем в этой же системе в точке 2 приложим сосредоточенную силу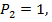 
зафиксировав в точке 1 перемещение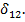 
Перемещения, вызываемые единичными силовыми факторами – сосредоточенными силами или моментами, в дальнейшем станем называть единичными и обозначать буквой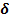 
, а любые другие – буквой 
. Тогда единичное перемещение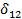 
- это перемещение во втором состоянии по направлению единичной силы 
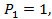вызванное силой 
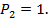Аналогично, единичное перемещение 
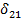- это перемещение в первом состоянии по направлению единичной силы 
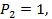вызванное силой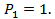 
| P1 |
| j |
| * |
| 2 |
| * |
| 1 |
|
| P2 |
| k |
| 1 |
| 2 |
| * |
| * |
|
| Рис.4.12 |
Применим к рассмотренным состояниям упругой системы теорему о взаимности работ. В результате получим:
.
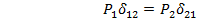Так как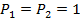 
то:
,
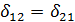или в общем виде
.
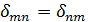ТЕОРЕМА МАКСВЕЛЛА. Для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй единичной силы, вызванному первой единичной силой.
Определение перемещений
Рассмотрим два состояния упругой системы. Первое состояние этой системы вызвано действием силы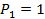 
и названо единичным ( рис.5.1).
Второе состояние вызвано действием некой внешней нагрузки и названо действительным.
| P1 |
| j |
| * |
| k |
| 1 |
| * |
|
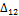
| Рис.5.1 |
Запишем выражение для работы сил первого состояния на перемещениях, вызванных силами второго состояния: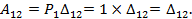 
Используя выражение для работы 
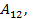записанное через внутренние усилия, полученное выше, получим формулу для вычисления перемещения в точке при действии произвольной внешней нагрузки:
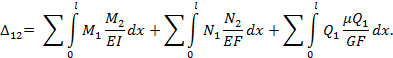
В вышеприведенной формуле 
- ординаты эпюр, соответственно, изгибающих моментов, продольных и поперечных сил т.н. «единичного» состояния, при действии на заданную упругую систему единичной обобщенной силы. Такие эпюры называются единичными;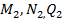 
- ординаты эпюр, соответственно, изгибающих моментов, продольных и поперечных сил действительного состояния системы, называемые «грузовыми».
Записанное в более общем виде выражение для определения перемещений, полученное выше, носит название интеграла или формулы Мора.
Если упругая система имеет постоянные поперечные сечения элементов,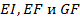 
могут быть вынесены за знак интегралов.
Последовательность определения перемещений.
1). Формируется т.н. единичное состояние путем приложения единичного силового фактора в расчетном сечении по направлению искомого перемещения. Следует иметь в виду, что при определении линейного перемещения в этих целях используют единичную силу. При определении же угла поворота в расчетном сечении прикладывают единичный момент. При приложении единичного силового фактора направление его действия ничем не регламентируется. Истинное же направление перемещения регулируется с помощью правила знаков, о котором будет сказано ниже.
2) Производится построение необходимых единичных эпюр. При этом влиянием внешней нагрузки на систему пренебрегают.
3) Производится построение необходимых грузовых эпюр.
4) Производится интегрирование по участкам системы и вычисляется нужное перемещение.
Обратим внимание на упрощение процесса определения перемещений для некоторых видов конструкций.
Для конструкций, работающих на изгиб, а такими являются балки, рамы, влиянием поперечных и продольных сил на величину перемещений пренебрегают.
В фермах при определении перемещений учитывают только продольные силы.
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ ТЕПЛОВОГО ВОЗДЕЙСТВИЯ.
Преобразуем формулу Мора для определения перемещений следующим образом:
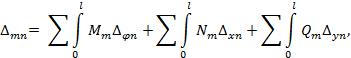
где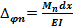 
– взаимный угол поворота торцевых сечений элемента 
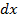стержня от заданной нагрузки;
– взаимное смещение торцевых сечений элемента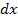 
стержня вдоль его продольной оси;
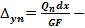взаимный сдвиг торцевых сечений элемента 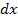стержня.
В таком преображенном виде формула Мора может быть использована для исследования деформаций элемента 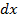от воздействия теплового поля, а в дальнейшем и для определения перемещений всей системы от данного внешнего воздействия (рис.5.2). Следует обратить внимание на то, что распределение теплового поля по высоте сечения подчиняется линейному закону, а 
.
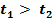Как это следует из рис5.2, удлинение верхнего вол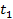окна за счет температуры 
- 
а, соответственно, нижнего волокна за счет температуры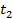 
- 
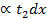. Осевое удлинение в этом случае составит
Взаимный угол поворота торцевых сечений элемента 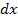ввиду малости удлинений равен тангенсу угла наклона сечений относительно вертикальной оси:
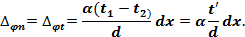
При действии подобного теплового поля деформаций сдвига в элементе 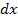не возникает.
Запишем формулу Мора для теплового воздействия с учетом всего вышеприведенного:
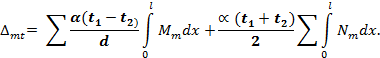
Суммирование производится лишь по тем элементам, которые подвержены нагреву!
Для прямолинейных и ломаных стержней постоянного сечения интегралы представляют собой не что иное, как площади эпюр единичного состояния, подсчитанные только на нагретых стержнях. Тогда выражение для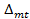 
приобретает более простой вид:
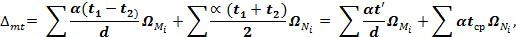
где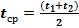 
– температура среднего волокна;
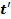- перепад температур на крайних волокнах элемента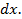 
При определении перемещений от теплового воздействия действуют следующие правила знаков:
- при вычислении составляющей перемещения, зависящей от площади эпюры моментов единичного состояния, ему присваивают знак «плюс», если эпюра расположена со стороны более высокой температуры, и, наоборот;
- при вычислении составляющей перемещения, зависящей от площади эпюры продольных сил единичного состояния, ему присваивают знак «плюс», если знак эпюры и знак средней температуры совпадают, и, наоборот.
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ОТ КИНЕМАТИЧЕСКОГО СМЕЩЕНИЯ ОПОР ( ОСАДКИ ОПОР ).
Следует заметить, что при кинематических смещениях опор статически определимых систем по направлению их опорных закреплений внутренние усилия в них не возникают. Различают два типа осадок опор: линейные, связанные с перемещениями опорных стержней шарнирно-подвижных, шарнирно-неподвижных опор и жестких «заделок» по вертикали, горизонтали и пр., а также угловые, связанные с поворотом жестких «заделок» (опор в виде жесткого защемления). Причины, по которым становятся возможными подобные ненормативные осадки, различны. Это и ошибки при расчетах фундаментов, неверная оценка геоподосновы, деформации намокших глинистых грунтов при замораживании и т.д.
|
|
|
| i |
| i |
| i |
| i |
|
|
|
| Рис.5.3 |
Рассмотрим два состояния упругой системы (рис.5.3). В первом случае рассмотрим действительное состояние, возникшее от вертикальной осадки правой шарнирно-подвижной опоры, величиной С, как бы от «нулевой нагрузки». Во втором случае по некоторому направлению i прикладываем единичную силу (единичное состояние), с целью определить линейное перемещение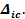 
На основании теоремы о взаимности работ для рассмотренных на рис.5.3 состояний, в одном из которых сооружение не загружено (как бы под влиянием вышеупомянутой «нулевой» нагрузки) запишем следующее:
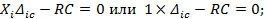
В случае нескольких кинематических воздействий и с учетом правила знаков, приведенного ниже, формула для вычисления перемещений от осадки опор (последняя составляющая универсальной формулы Мора) принимает такой окончательный вид:
|
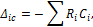
где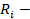 
величина реакции, взятая с единичного состояния по направлению заданной осадки опор;
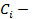величина соответствующей ей осадки опор.
При этом знак реакции – «плюс», если её направление совпадает с направлением соответствующей осадки опор, и, наоборот.
ПРАВИЛО ВЕРЕЩАГИНА (СПОСОБ «ПЕРЕМНОЖЕНИЯ» ЭПЮР).
В 1925 году отечественным инженером Верещагиным был предложен революционный прием, позволивший во многих случаях избежать прямого интегрирования при использовании формулы Мора для определения перемещений от внешней нагрузки – способ «перемножения» эпюр. При этом одна из «перемножаемых» эпюр обязательно должна быть прямолинейной. Суть предложенной новации заключалась в следующем. Рассмотрим это на таком примере.
Имеются фрагменты двух эпюр на некотором участке рассчитываемой конструкции (рис.5.4.), причем положение центра тяжести криволинейной эпюры, так же, как и её площадь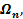 
нам известны.
| }Mn |
| }yc |
| }Mm |
| dx |
| ц.т. |
|
|
|
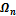
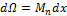
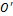
| O |
| α |
|
|
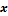
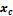
| Эпюра Mn |
| Эпюра Mm |
| Рис.5.4 |
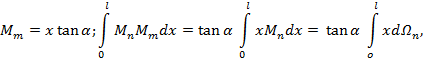
где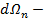 
дифференциал площади эпюры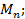 
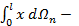статический момент площади 
относительно оси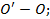 
.
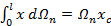В этом выражении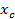 
- абсцисса центра тяжести фигуры 
.
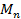Так как
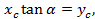
То 
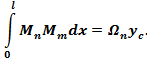
| Результатом “перемножения» двух эпюр является произведение площади одной из них на ординату с другой эпюры (обязательно прямолинейной), взятую под центром тяжести первой эпюры. |
Результат перемножения (а, следовательно, и вычисляемое перемещение) положителен, если первая эпюра и соответствующая ордината со второй эпюры расположены по одну сторону от нейтральной оси, и, наоборот.
Большим преимуществом правила Верещагина является возможность свести многие простые случаи перемножения двух прямолинейных эпюр к табличной форме.
| Ц.Т |
| 2/3М2 |
| Рис. 5.5 |
| М1 |
| М2 |
| 1/3l |
| 2/3l |
| 1/3l |
| 2/3l |
| l |
| l |
| а) |
| Ц.Т |
| М1 |
| 1/3М2 |
| М2 |
| 1/3l |
| 2/3l |
| 1/3l |
| 2/3l |
| l |
| l |
По этому правилу очень удобно перемножать треугольного вида эпюры, центр тяжести которых находится на расстоянии 2/3 длины. При этом возможны два варианта: Если нулевые значения эпюр расположены с одной стороны (рис. 5.5а) то интеграл будет равен:
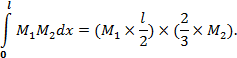
Если нулевые значения эпюр расположены с разных сторон (рис. 5.5б) то интеграл будет равен:
| Рис. 5.6 |
| М1 |
| М2 |
| М1 |
| М2 |
| М1 |
| М2 |
| М3 |
| М3 |
| М3 |
| М3 |
| М4 |
| М4 |
| М5 |
| М6 |
| а) |
| б) |
| в) |
| l |
| l |
| l |
По этому правилу также удобно перемножать трапециевидную эпюру на прямоугольную (рис. 5.6а ).
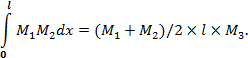
Перемножение двух трапециевидных эпюр удобнее выполнять не по правилу Верещагина, а по следующей формуле (рис. 5.6б ):
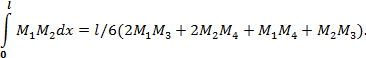
Для перемножения параболической эпюры изгибающих моментов от равномерно распределенной нагрузки на трапециевидную эпюру можно использовать формулу Симпсона(рис. 5.6в ):
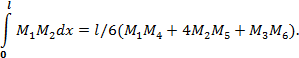
При использовании всех вышеприведенных формул необходимо учитывать знак, если перемножаемые значения лежат с разных сторон от оси стержня, то надо поставить знак минус.
| F=10кН |
| q=4кН/м |
| m=20кН.м |
| Рис. 5.7 |
| 4м |
| 3м |
| А |
| В |
| С |
| D |
| Е |
Для примера определим вертикальное перемещение точки А в раме показанной на рисунке 5.7. Для этого построим эпюру изгибающих моментов от внешней нагрузки (рис. 5.8а) и эпюру изгибающих моментов от вертикальной сосредоточенной силы, приложенной в точке А (рис. 5.8б).
При перемножении эпюры изгибающих моментов от внешней нагрузки Мр на единичную эпюру изгибающих моментов М1 от силы F1 = 1, мы будем иметь два участка ЕD и DC. На участке ЕD надо перемножить криволинейную эпюру на треугольную. Для этого используем формулу Симпсона. На другом участке одна эпюра трапециевидная, а другая треугольная. Здесь можно использовать формулу перемножения трапеции на трапецию.
| Рис. 5.8 |
| (кН·м) |
| 92 |
| 20 |
| 60 |
| 60 |
| 32 |
| 60 |
| Мр |
| 68 |
| (м) |
| 4 |
| F1=1 |
| М1 |
| б) |
| а) |
yA=Sò(MрM1)/(EJ)ds=4/(6EJ)(92×4+4×68×2)+
+3/(6EJ)(32×4×2+4×20)=776/(EJ)(м).
В этой же точке А определим угол поворота. Эпюра изгибающих моментов Мр от внешней нагрузке уже была построена (рис.5.8а ). Остается построить только новую эпюру изгибающих моментов М2 от единичного момента, приложенного в сечении А (рис. 5.9а).
При перемножении единичной эпюры М2 на эпюру Мр,, мы будем иметь три участка АЕ, ЕD, DC. На первом участке АЕ перемножаем треугольник на прямоугольник по правилу Верещагина. На втором участке ЕD перемножаем параболу и прямоугольник по правилу Симпсона. И на последнем участке DC перемножаем трапецию на треугольник по формуле перемножения трапеции на трапецию. В результате мы получим следующий угол поворота
jA=Sò(MрM2)/(EJ)ds=60×6/(2EJ)× 1+
+4/(6EJ)×(60×1+4×68×1+92×1)+
+3/(6EJ)×(32×2×2+1×20)=504,67/(EJ).
Для определения горизонтального перемещения в точке В, строим новую единичную эпюру изгибающих сил М3 от горизонтальной единичной силы F3 = 1 (рис.5.9б). Искомое перемещение будет равно:
yB=Sò(MрM3)/(EJ)ds=60×6/(2EJ)×2/3× 6+
+60×6/(2EJ)×6+
+4/(6EJ)×(60×6+4×68×6+92×6)=3856/(EJ ).
| Рис. 5.9 |
| 6 |
| 1 |
| 1 |
| 1 |
| 1 |
| М2 |
| m=1 |
| (м) |
| 6 |
| F3=1 |
| М3 |
| б) |
| а) |
Библиографический список
1. Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики стержневых систем. -М.: АСВ, 1996.-541с.
2. Анохин Н.Н. Строительная механика в примерах и задачах часть 1. -М.: АСВ, 1999.-334с.
3. Анохин Н.Н. Строительная механика в примерах и задачах часть 2. -М.: АСВ, 2000.-462с.
4. Дарков А.В., Шапошников Н.Н. Строительная механика. -М.: Лань, 2008. -656с.
5. Александров А.В., Потапов В.Д. Строительная механика . -М.: Высшая школа, 2007. -511с.
Оглавление
1. Введение…………………………………………………………………… 2
2. Кинематический анализ сооружений……………………………… 8
3. Расчет статически определимых систем………………………… 13
4. Основные теоремы об упругих системах………………………….. 32
5. Определение перемещений………………………………………………41
Дата добавления: 2018-06-01; просмотров: 1732; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!