Условные вероятности и теорема умножения

Стр 1 из 21Следующая ⇒

Nbsp;

ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС

«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»

Учебное пособие по курсу

«Теория вероятностей и математическая статистика/Статистика.Теория статистики»

Москва

2014

Рекомендовано к изданию

Решением Ученого совета ИМЭС

(Протокол № 4 от 27 ноября 2014 г.)

Настоящее учебное пособие разработал кандидат физико-математических наук, доцент, заведующий кафедрой математики и информатики ИМЭС Налимов Валерий Николаевич.

ПРЕДИСЛОВИЕ

Настоящее учебное пособие предназначено для студентов второго курса заочной формы обучения и по тематическому объему полностью соответствует требованиям рабочей программы учебной дисциплины «Теория вероятностей и математическая статистика», которая, в свою очередь, полностью соответствует требованиям действующего федерального государственного образовательного стандарта по направлению 38.03.01 «Экономика».

Порядок изложения разделов, тем и основных подразделов тем в данном учебном пособии соответствует порядку, принятому в рабочей программе учебной дисциплины «Теория вероятностей и математическая статистика». Однако нумерация тем и подразделов в настоящем пособии может отличаться от нумерации, принятой в учебном пособии [1].

По каждой теме и подразделу темы данное пособие содержит теоретический материал, изложенный в предельно сжатой форме (теоремы и аксиомы, математические факты, формулы и их следствия, имеющие практическую значимость), а также примеры использования этого материала для решения задач. В конце изложения теоретического материала каждой темы приведены вопросы для самопроверки знаний по этой теме курса. Некоторые темы курса заканчиваются вопросами в форме тестов.

После ознакомления с теоретическим материалом студенту следует кратко и четко ответить на вопросы, самостоятельно оценив и отобрав материал, изложенный в литературе, ссылки на которую приведены в конце каждой темы, или подраздела, а полный список литературы приводится в конце пособия. Ваши ответы должны быть размещены непосредственно в Вашем экземпляре пособия. Причем при тестовом варианте ответов на вопросы Вы должны поставить любой значок (крестик, галочку и т.п.) только в одном квадрате, соответствующем верному, на Ваш взгляд, ответу на поставленный вопрос.

Настоящее пособие может быть полезно студентам второго курса заочного отделения, обучающимся по направлению 38.03.02 «Менеджмент», при подготовке к экзамену по курсу «Теория статистики», а также студентам второго курса очного (дневного) и очно-заочного отделений ИМЭС, при подготовке к сдаче экзаменов по дисциплинам «Теория вероятностей и математическая статистика» и «Теория статистики».

ЛИСТ СТУДЕНТА

Фамилия ___________________________________

Имя ________________________________________

Отчество ____________________________________

Факультет ___________________________________

Курс _________________________________________

Группа _______________________________________

Дата начала работы: «_____» _____________ 20___ г.

Дата окончания работы «_____» ______________ 20___ г.

Личная подпись _________________________

ЛИСТ РЕЦЕНЗИИ

Рецензент ______________________

______________________

«_____» _______________ 20____ г.

РАЗДЕЛ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Тема 1.1. События и вероятность

Элементы комбинаторики

Упорядоченным называется множество, в котором указан порядок следования элементов.

ПРИМЕР: Множества (a, b, c) и (a, c, b) есть различные упорядоченные множества, состоящие из одних и тех же трех элементов.

Сформулируем основные правила комбинаторики.

1. Правило суммы. Пусть из множества А элемент а₁ можно выбрать n₁ способами, элемент а₂ – другими n₂ способами, а элемент а₃ – n₃ способами, отличными от предыдущих. Тогда выбор одного из элементов а₁, или а₂, или а₃ можно осуществить (n₁ + n₂ + n₃) способами.

ПРИМЕР:Пусть в корзине содержится 7 апельсинов, 5 бананов и 10 яблок. Тогда выбор одного из фруктов (или апельсина, или банана, или яблока) можно сделать 22 способами (7 + 5 + 10 = 22).

2. Правило произведения. Пусть из множества А элемент а₁ можно выбрать n₁ способами, а после этого выбор элемента а₂ можно осуществить n₂ способами, а после этого выбор элемента а₃ можно осуществить n₃ способами. Тогда все три элемента в указанном порядке могут быть выбраны способами.

ПРИМЕР:Пусть в спортивном велосипеде имеются 3 ведущие звездочки и 4 ведомые. Сколько всего передач имеется в велосипеде?

Очевидно, что каждая передача определяется выбором одной ведущей и одной ведомой звездочки. Следовательно, число всех передач совпадает с числом выборов одного элемента из трех и другого элемента из четырех и равно: 3 ∙ 4 = 12.

Пусть некоторое множество А содержит n элементов. Каждое его упорядоченное подмножество, состоящее из k элементов, называется размещением из n элементов по k элементов. Число всех таких размещений обозначается (читается: «А из эн по ка») и определяется по формуле: .

ПРИМЕР:Сколько сигналов можно составить из 6 флажков различного цвета, взятых по два?

Очевидно, что два разноцветных флажка в разном порядке будут соответствовать двум различным сигналам. Поэтому искомое число есть число размещений из 6 по 2, т.е.

Размещение из n элементов по n элементов называется перестановками из n элементов. Число всех таких перестановок обозначается и определяется по формуле: .

ПРИМЕР: Сколько трехзначных чисел можно образовать из цифр 1, 2 и 3, если каждая из них может входить в изображение числа только один раз?

Очевидно, что искомое число есть число перестановок из 3 элементов, равное: .

Пусть некоторое множество А содержит n элементов. Каждое его неупорядоченное подмножество, состоящее из k элементов, называется сочетанием из n элементов по k элементов. Число всех таких сочетаний обозначается (читается: «цэ из эн по ка») и определяется по формуле: .

ПРИМЕР: Сколькими способами можно выбрать два шара из ящика, содержащего 8 шаров?

Очевидно, что искомое число способов будет равно числу сочетаний из 8 элементов по 2 элемента, т.е.

Достаточно несложно (убедитесь в этом сами) показать справедливость еще одной полезной формулы комбинаторики:

События

Эксперимент, испытание, опыт, процесс – это возникновение или преднамеренное создание определенного комплекса условий S, результатом которого является тот или иной исход.

Событием называется исход испытания. Это понятие является основным в теории вероятностей. События принято обозначать заглавными латинскими буквами А, В, С и т.д.

Среди всех событий выделяют достоверное и невозможное события. Достоверным называется событие Ω, которое обязательно произойдет при выполнении данного комплекса условий S, т.е. в результате испытания. Невозможным называется событие Ø, которое заведомо не произойдет при выполнении данного комплекса условий S, т.е. в результате испытания.

ПРИМЕРЫ:Событиями являются: выпадение орла при бросании монеты, выигрыш по облигации или лотерейному билету, увеличение курса доллара в следующем месяце и т.д.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другие.

Элементарными называются те из событий, которые невозможно разложить на составляющие их события. При этом любое событие можно составить из элементарных событий.

ПРИМЕР: При бросании игральной кости элементарными событиями являются выпадения чисел 1, 2, 3, 4, 5, 6. В этом же опыте событием является выпадение четного числа очков, которое может быть составлено из элементарных событий – выпадения 2, 4 и 6 очков.

Понятие вероятности

Представление о случайности событий связано с невозможностью предсказания исхода того или иного испытания. Однако, например, при многократном бросании монеты выясняется, что примерно в половине случаев выпадает герб. При исследовании большого количества результатов одинаковых испытаний обнаруживаются определенные закономерности, которые можно описать, используя понятие вероятности.

Под вероятностью события понимается некоторая числовая характеристика возможности наступления этого события в результате испытания. Существует несколько подходов к определению вероятности.

1. Статистическое определение вероятности.

Пусть при проведении n испытаний некоторое событие А появилось ровно m раз. Относительной частотой этого события называется отношение W(A) = m / n. Многочисленные эксперименты такого рода показывают, что при больших значениях n относительная частота изменяется мало и остается практически постоянной.

Статистической вероятностью события называется постоянная величина, вокруг которой колеблются значения относительной частоты при неограниченном возрастании числа испытаний.

ПРИМЕР: Английский ученый К. Пирсон произвел 23000 бросаний монеты. При этом герб появился 11512 раз. Следовательно, относительная частота появления герба равна 11512/23000 = 0,5005. Этот пример показывает, что за статистическую вероятность появления герба можно взять число 0,5.

2. Классическое определение вероятности.

Классической схемой, или схемой случаев, называется испытание, в котором число элементарных исходов конечно и все они являются равновозможными.

Элементарный исход (событие) называется благоприятствующим событию А, если его появления влечет за собой наступление события А.

Классической вероятностью события А называется отношение числа m элементарных исходов, благоприятствующих событию А, к числу n всех элементарных равновозможных исходов испытания.

Из этого определения следует, что вероятность достоверного события Р(Ω) = 1, вероятность невозможного события Р(Ø) = 0, а вероятность любого случайного события А заключена в пределах: 0 ≤ Р(А) ≤ 1.

ПРИМЕР:При бросании игральной кости число всех возможных исходов n = 6 и все они являются равновозможными. Пусть событие А состоит в том, что в результате испытания (бросания) появится четное число очков. Тогда для этого события благоприятствующими будут исходы, состоящие в выпадении 2, 4 и 6 очков. Их количество m = 3. Поэтому вероятность события А будет равна P(A) = m / n = 3 / 6 = 1 / 2.

Алгебра событий

Событие А влечет за собой событие В, если из наступления события А непременно следует наступление события В. Этот факт обозначается .

ПРИМЕР:Пусть производится выбор одного из чисел от 1 до 100. Пусть событие В означает выбор четного числа, а событие А – выбор числа, кратного 10. Тогда , т.к. каждое число, кратное 10, является четным.

Равенство событий А = В означает, что и , т.е. эти события состоят из одних и тех же элементарных событий (исходов).

ПРИМЕР:Пусть производится выбор одного из чисел от 1 до 100. Пусть событие В означает выбор числа, кратного 3, а событие А – выбор числа, сумма цифр которого делится на 3. Тогда по признаку делимости на 3 можно записать А = В.

Суммой событий А и В называется событие С = А + В, состоящее в появлении либо события А, либо события В, либо обоих этих событий.

ПРИМЕР: Из орудия производятся два выстрела. Пусть событие А – попадание при первом выстреле, а событие В – попадание при втором выстреле, тогда событие С = А + В – попадание при первом, либо при втором, либо в обоих выстрелах.

Произведением событий А и В называется событие С = А∙В, состоящее в совместном появлении (совмещении) этих событий.

ПРИМЕР:Если событие А – деталь годная, а событие В – деталь окрашенная, то событие А∙В – деталь годная и окрашенная.

Несовместными называются события А и В, если их произведение является невозможным событием, т.е. А∙В = Ø.

Дополнением к событию А (или противоположным событию А событием) называется событие 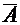, которое можно определить равенствами: Ø и .

ПРИМЕР: При бросании монеты выпадение герба и выпадение надписи будут несовместными событиями. Одновременно событие выпадение надписи будет дополнением к событию выпадение герба.

Разностью событий А и В называется событие, состоящее в наступлении А и не наступлении В. Разность характеризуется условием .

Теорема сложения

Пусть А и В несовместные события. Вероятность их суммы равна сумме их вероятностей:

Р(А + В) = Р(А) + Р(В).

Для произвольных событий верна более общая теорема:

Р(А + В) = Р(А) + Р(В) – Р(А∙В).

ПРИМЕРЫ:

1. В урне находятся 30 шаров, из них 10 красных, 5 синих и 15 неокрашенных шаров. Найти вероятность извлечения из урны цветного (окрашенного) шара.

Появление цветного шара в одном испытании – это появление либо красного (событие А), либо синего (событие В) шара, т.е. сумма этих событий. С другой стороны появление красного шара исключает появление синего шара в одном испытании, т.е. эти два события несовместны.

Вероятность события А равна: Р(А) = 10 / 30 = 1 / 3, а события В соответственно: Р(В) = 5 / 30 = 1 / 6. Подставив эти вероятности в формулу теоремы сложения для несовместных событий, получим:

2. В магазин могут поступать товары с двух складов. Вероятности поступления товаров с этих складов соответственно равны 0,4 и 0,5. Найти вероятность поступления в магазин товаров хотя бы из одного из двух складов.

Событие А (товары поступили с первого склада) и событие В (товары поступили со второго склада) независимы, но совместны, поскольку допускается поступление товаров с двух складов одновременно. Поэтому искомая вероятность суммы этих двух событий будет равна:

Здесь использована формула теоремы умножения вероятностей для независимых событий , которая приводится в подразделе 1.1.6.

Поскольку события 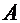и 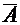несовместны, а их сумма есть достоверное событие, вероятность которого равна 1, можно записать:

Условные вероятности и теорема умножения

На практике часто встречаются ситуации, когда наступление некоторого события значительно меняет возможности наступления других событий и их вероятности. Такие события называются зависимыми. Если произошло событие В, то новая вероятность события А (вычисленная при условии, что событие В уже наступило) называется условной вероятностью, обозначается и определяется формулой (при ):

Опираясь на эту формулу и учитывая симметрию событий А и В, получают формулы теоремы умножения, которые имеют для зависимых событий А и В вид:

Независимыми называются события А и В, для которых выполнены условия: или . Для независимых событий теорема умножения принимает вид:

ПРИМЕРЫ:

1. На склад поступило 35 холодильников. Известно, что 5 из них неисправны, но неизвестно какие именно. Найти вероятность того, что 2 взятых наугад холодильника окажутся неисправными.

Вероятность того, что первый выбранный холодильник окажется неисправным (событие А) вычислим непосредственно Р(А) = 5/35 = = 1/7.

Если первый холодильник оказался неисправным, то вероятность того, что второй холодильник окажется неисправным (событие В) рассчитаем как условную вероятность:

Искомую вероятность совмещения этих событий найдем по первой из формул теоремы умножения:

2. Вероятность попадания в цель при стрельбе из каждого из двух орудий составляет 0,8 и 0,7 соответственно. Найти вероятность промаха при одном залпе (одновременном выстреле) из двух орудий.

Вероятность промаха первого орудия (событие А) равна Р(А) = 0,2, а второго (событие В) – Р(В) = 0,3. События А и В совместные и независимые, поэтому искомую вероятность их совмещения находим по второй формуле теоремы умножения:

Дата добавления: 2018-06-01; просмотров: 451; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!