Алгоритм случайного множественного доступа «АЛОХА».
Рассмотрим простейший способ:
Абонент, который имеет готовое для передачи сообщение, передает это сообщение в начале очередного окна с некоторой вероятностью 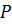 – параметр алгоритма. В рамках наших допущений знаем только то, что происходит в данный момент.
– параметр алгоритма. В рамках наших допущений знаем только то, что происходит в данный момент.
4) Предположим, что в системе имеется M абонентов. У каждого абонента имеется 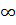 очередь. На вход системы поступает поток интенсивности
очередь. На вход системы поступает поток интенсивности 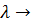
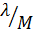 . При этом поток сообщений, который поступает от каждого сообщения -
. При этом поток сообщений, который поступает от каждого сообщения - 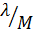 .
.
 1
1 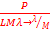
P
 2 P канал
2 P канал
 P
P
 М
М
Рис. 3.2. Модель алгоритма случайного множественного доступа
Анализ алгоритма АЛОХА на качественном уровне.
d
Р.В
АЛОХА


d0
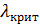 1
1 
Рис. 3.3. Сравнение АЛОХА и алгоритма с разделением времени
Пусть Nt – число абонентов, у которых к началу окна t в очереди есть хотя бы 1 сообщение. Это активные абоненты.
Nt 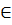
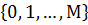
Pr 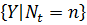 = = Pr
= = Pr 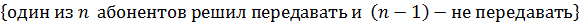 =
= 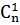 p
p 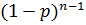 =
= 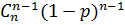
Вычислим вероятность – успех при условии, что в начале окна было n активных абонентов.
Предположим, что известно число активных абонентов к началу окна.
1 из n абонентов решил передавать.
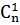 – число способов выбора одного абонента из n
– число способов выбора одного абонента из n
2 допуск 3 лабораторной работы:
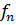 (p) = np
(p) = np 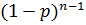 – max - ? (P
– max - ? (P 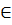
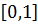 Ответ:
Ответ: 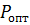 =
=  ).
).
Pr 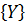 = n
= n 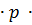
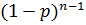 =
= 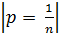 = n
= n 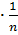
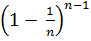 = ?
= ?
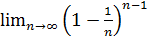 = е-1 = 0,36 =
= е-1 = 0,36 = 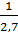 е ≈ 2,7
е ≈ 2,7
Задача: нахождение  кр
кр
Для нахождения  кр рассмотрим ситуацию, когда у всех абонентов имеется готовое для передачи сообщение. Опишем данную систему как СМО
кр рассмотрим ситуацию, когда у всех абонентов имеется готовое для передачи сообщение. Опишем данную систему как СМО
1

n у п к к п у

Рис 3.3. Система, в которой у всех абонентов есть сообщения
N = 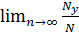 = Pr
= Pr 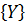 – вероятность успеха = Мр
– вероятность успеха = Мр 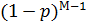
Интенсивность обслуживания - можно сказать, средняя доля успеха.
Интенсивность успеха – средняя доля окон, в которых произошел успех.

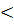 М
М  P
P 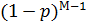
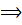
 кр = М
кр = М  P
P 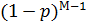
Вспомним: Pr 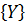 = n
= n 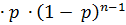 = f(p,n)
= f(p,n)
f(p)  max, Pопт =
max, Pопт = 
d
С увеличением интенсивности 
увеличивается задержка d
d0

 кр
кр
Рис 3.4. График зависимости задержки от интенсивности
1
2 канал

М
Рис. 3.5. Общее описание системы
Необходимо найти  кр. Для нахождения
кр. Для нахождения  кр рассмотрим ситуацию, когда очереди заполнены у всех абонентов (рис.1)
кр рассмотрим ситуацию, когда очереди заполнены у всех абонентов (рис.1)
1 р
р
2 канал

р
М
Рис.3.6. Описание системы, в которой у всех абонентов есть сообщения для передачи
В этом случае систему можно описать упрощенно (рис.2). Причем 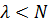 , чтобы система была устойчивой
, чтобы система была устойчивой
N = 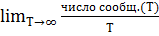
Nу(Т) – число успехов по длине Т
Nк(Т) – число конфликтов по длине Т
Nп(Т) – число пусто по длине Т
У П К У К … У
Т
Рис. 3.7. Упрощенное описание системы
Ny(Т)+Nк(Т)+Nп(Т) = Т
lim 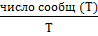 =
= 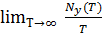 =
= 
Следовательно, 
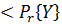 = M
= M  P (1
P (1  P)M-1 =
P)M-1 =  кр(М,Р)
кр(М,Р)
 кр(М,Р)
кр(М,Р)  (POPT =
(POPT =  )
)
max
 кр(М,
кр(М,  ) = М
) = М 
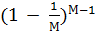
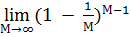 = е-1
= е-1  0,36
0,36
Разберемся с начальной задержкой d0.
Для максимального d0 рассмотрим ситуацию, когда у первого абонента появляется сообщение.
В этом случае временная диаграмма будет иметь следующий вид:
 D
D
П П П П П ......... У
P P P
Рис 3.8. Временная диаграмма после появления сообщения у первого абонента
D2 = D – D1( Абонент решает с вероятностью Р).
В окне с номером t может быть либо «пусто», либо «успех».
D1 – непрерывная случайная величина
D1 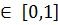
 М
М 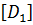 =
= 
D2 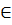
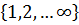
Pr 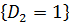 = P
= P
Pr 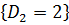 = (1-P)P
= (1-P)P
Pr 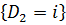 =
= 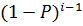 P
P
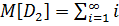 -Pr
-Pr 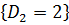 =
= 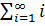
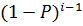 P =
P = 
Допуск 3 3-ей лабораторной работы: проверить значение 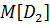 .
.
d0 = M 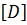 =
=  +
+ 
d
М = 100, Р = 
М = 100, Р 

0,1 
МР(1 -  )
) 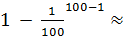 0,36
0,36
Рис. 3.9. Анализ алгоритма на качественном уровне
Выбор Р =  решает выбор
решает выбор 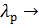 max, но не решает d(
max, но не решает d(  )
)  min
min
Выбор параметра Р - вероятность передачи - сильно влияет на характеристики алгоритма «АЛОХА». Самое существенное: выбор Р =  не является оптимальным в смысле минимума средних задержек.
не является оптимальным в смысле минимума средних задержек.
Дата добавления: 2018-06-01; просмотров: 1341; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
