Калибровка (градуировка) средств измерений
В данном разделе рассматриваются и определяются те метрологические характеристики СИ, которые необходимы для получения измеренного значения величины. Калибровка СИ связана с получением единицы величины от эталона и дальнейшего ее хранения для выполнения будущих измерений.
Единица измеряемой величины может быть сохранена отметками шкалы или параметрами калибровочной функции (КФ) – градуировочной характеристики (ГХ), соединяющей показания СИ с измеряемой величиной, или параметрами калибровочно-поправочной функции (КПФ), связывающей показания СИ с измеряемой и одной влияющей величиной или несколькими влияющими величинами.
Если КФ и КПФ не несут информации о показателях точности их построения, то они не могут быть использованы для представления результата измерения. С КФ и КПФ связана погрешность калибровки (погрешность эталона), представляемая в виде таблицы или функции. Стабильность КФ и КПФ во времени выполняют периодической поверкой СИ.
Диаграмма калибровки – графическое выражение соотношения между показанием СИ и соответствующим эталонным значением величины с полосой погрешности. Она соответствует отношению «один-множество», а ширина полосы для данного показания отражает инструментальную погрешность.
Калибровочные функции
Значительная часть скважинной геофизической аппаратуры относится к индивидуально градуируемым СИ.
|
|
|
Градуировкойизмерительного преобразователя называется совокупность операций, выполняемых с целью передачи ему единицы физической величины путем оцифровки шкалы прибора или установления параметров функциональной зависимости между измеряемым параметром и выходным сигналом измерительного преобразователя. Следует заметить, что в Законе № 102-ФЗ термин «градуировка» не упоминается. Эту операцию будем рассматривать как составную часть калибровки(см. рис. 13), в результате которой определяются действительные значения параметров индивидуальной КФ.
Градуировочной характеристикой называется зависимость выходного сигнала х СИ от измеряемого параметра (измеряемой величины) Визм, то есть
x = f(Визм). В международном словаре VIM3 градуировочной характеристике соответствует понятие «калибровочная функция».
ГХ в таком виде неудобна при выполнении измерений, так как имеем выходной сигнал, а ищем измеренное значение. Поэтому в геофизике вместо ГХ принято строить и использовать КФ в виде зависимости измеряемой величины от выходного сигнала аппаратуры, то есть Визм = F(х). Она строится по эталонным значениям измеряемого параметра и выходным сигналам СИ, вызванным взаимодействием датчика (зонда) с эталоном.
|
|
|
Такая КФ, представленная формулой, очень удобна для непосредственного вычисления измеренного значения измеряемой величины по значению выходного сигнала геофизической аппаратуры.
КФ может быть номинальной (одинаковой для всей совокупности однотипных измерительных преобразователей) или индивидуальной (различной для каждого экземпляра однотипной аппаратуры). Аппаратура электрического и акустического каротажа, инклинометры и каверномеры имеют номинальные КФ. Для аппаратуры интегрального гамма-каротажа, нейтронного каротажа, плотностного гамма-гамма-каротажа, для скважинных термометров, манометров и расходомеров обычно строится индивидуальная КФ.
При градуировке всегда оцениваются погрешности построенной КФ, включающие погрешности применяемых эталонов и погрешности аппроксимации реальной экспериментальной функции преобразования какой-либо известной функцией.
КФ может быть линейной или нелинейной, функцией одной, двух и более переменных.
Если линейная КФ проходит через ноль (начало декартовых координат), то в документации указывается только один коэффициент преобразования. Если она не проходит через ноль, то указывают формулу Y = а + вх, описывающую функцию преобразования двумя коэффициентами а и в,х – выходной сигнал.
|
|
|
Если характеристика нелинейная, то чаще всего указывают функцию преобразования в виде полинома второй степениY = а + вх + сх2 (с тремя коэффициентами) и (или) график функции. Полином более высокой степени не используется, так как степень кривизны функции обычно невелика. Реже используется степенная и логарифмическая КФ.
При определении (вычислении) коэффициентов КФ как функции одной переменной составляется система уравнений, в каждом из которых неизвестными являются сами вычисляемые коэффициенты для каждой пары «измеряемый параметр - выходной сигнал».
Номинальную или индивидуальную КФ аппаратуры представляют в виде формулы, графика или таблицы. Но в любом случае в её основе лежит функциональная зависимость, связывающая измеряемую величину с выходным сигналом аппаратуры, а также с параметрами влияющих величин на основе экспериментальных данных.
Эти данные попарно представляют собой измеренные значения величины, воспроизводимые эталоном или измеренные эталонным прибором, и измеренные значения выходного сигнала градуируемой аппаратуры. Каждое из этих измеренных значений содержит систематическую погрешность, что обусловливает неидеальность процесса калибровки СИ. Это означает, что координаты каждой экспериментальной точки, принятой для построения КФ, являются случайными величинами. Поэтому принятая для аппаратуры КФ является частной реализацией совокупности случайных реализаций КФ, отличающихся от идеальной КФ этой аппаратуры.
|
|
|
Возможны два варианта расположения принятой КФ аппаратуры относительно экспериментальных точек:
1) проходит строго через экспериментальные точки;
2) проходит между экспериментальными точками, не совпадая ни с одной из них.
В первом случае количество пар экспериментальных данных равно числу неизвестных коэффициентов функции, принятой для аппаратуры в качестве КФ.
Для второго варианта число пар экспериментальных данных больше числа неизвестных коэффициентов КФ. В этом случае система уравнений не имеет однозначного решения и решается одним из статистических методов – методом наименьших квадратов (МНК).
Рассмотрим эти два способа построения КФ для трех видов функций, наиболее часто встречающихся в геофизике – линейной, параболической и логарифмической.
16.2 Способы построения линейной КФ вида Y = a + bх
Алгебраический способ
Исходные данные: эталон воспроизводит только два значения измеряемой величины 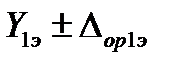 и
и 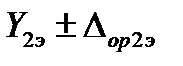 ; им соответствуют два измеренных значения выходного сигнала калибруемой аппаратуры
; им соответствуют два измеренных значения выходного сигнала калибруемой аппаратуры 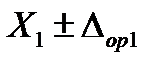 и
и 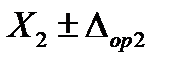 .
.
На основании таких исходных данных может быть составлена система двух линейных уравнений с двумя неизвестными a и b в следующем виде:
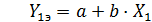 ,
,
 . (48)
. (48)
Эта система имеет однозначное решение:
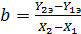 ,
,
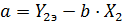 . (49)
. (49)
За оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается максимальная из двух нормированных (допускаемых) погрешностей эталонов (либо, 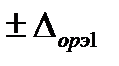 либо
либо  ), когда погрешностью измерений параметров выходного сигнала можно пренебречь. При этом должны выполняться неравенства:
), когда погрешностью измерений параметров выходного сигнала можно пренебречь. При этом должны выполняться неравенства:
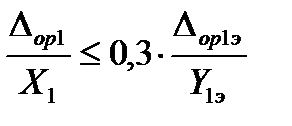 и
и 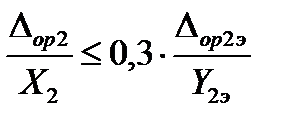 . (50)
. (50)
Если погрешностью измерений параметра выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается максимальное из следующих значений:
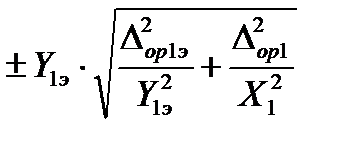 или
или 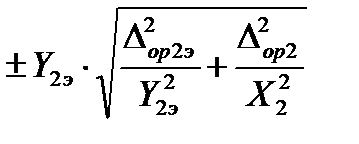 . (51)
. (51)
Частным случаем первого варианта построения линейной КФ является случай, когда функция проходит через начало координат. Такое возможно, когда по принципу действия, или благодаря схемным решениям аппаратуры, при нулевом значении измеряемого параметра выходной сигнал аппаратуры равен нулю. Эталон, например, полевой калибратор, воспроизводит только одно значение измеряемого параметра Y1э, которому соответствует только одно значение выходного сигнала калибруемой аппаратуры Х1. В итоге имеем одно линейное уравнение с одним неизвестным в следующем виде Y1э = bХ1, решение которого очевидно.
За оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается нормированная погрешность эталона ( 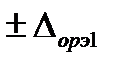 ), если погрешностью измерений параметров выходного сигнала можно пренебречь, то есть выполняется первое неравенство в (50). Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается:
), если погрешностью измерений параметров выходного сигнала можно пренебречь, то есть выполняется первое неравенство в (50). Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается:
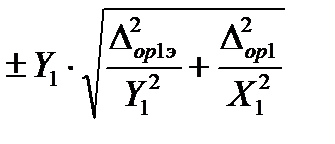 . 52)
. 52)
Статистический способ
Исходные данные: эталон воспроизводит более двух значений измеряемого параметра, например, для n значений 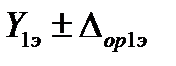 ,
, 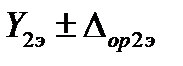 , … и
, … и  ; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры
; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры 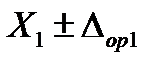 ,
, 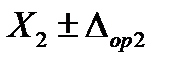 , … и
, … и  .
.
На основании таких исходных данных может быть составлена система n линейных уравнений с двумя неизвестными a и b в следующем виде:
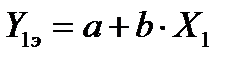
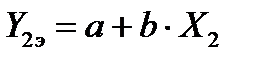 . (53)
. (53)
…
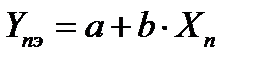
Эта система решается методом наименьших квадратов, предложенным Гауссом. Из неё составляют систему из двух нормальных уравнений с двумя неизвестными a и b. Нормальные уравнения получают по следующему правилу.
Первое нормальное уравнение получим в результате суммирования левой и правой частей системы (53), а второе в результате суммирования левой и правой частей этой системы после умножения каждого уравнения на коэффициент при неизвестном b. В итоге получим следующую новую систему двух нормальных уравнений:
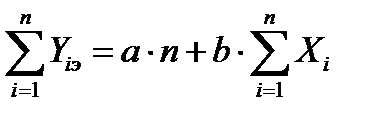 ,
,
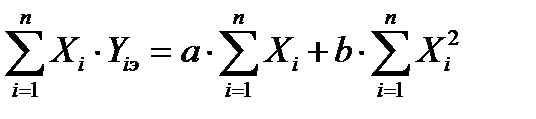 . (54)
. (54)
Решение данной системы нормальных уравнений найдём путём подстановки а из первого уравнения во второе, вычислим b и найдем а, подставив b в первое уравнение, или матричным способом.
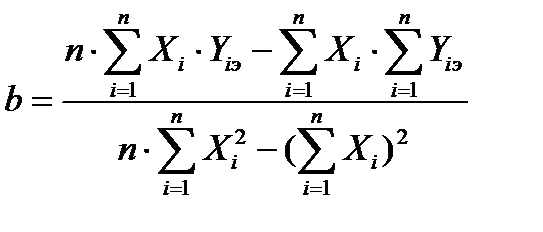 , (55)
, (55)
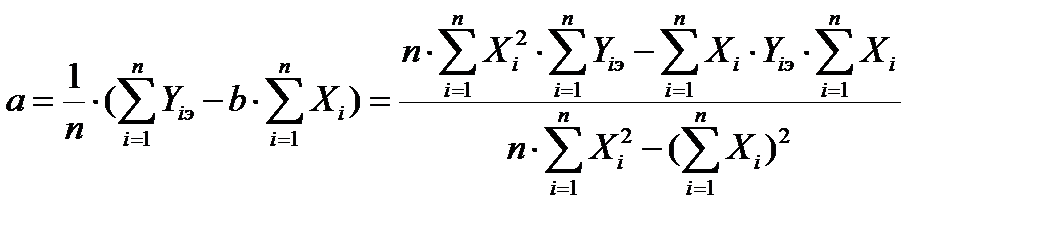 .
.
Частным случаем второго варианта построения линейной КФ является случай, когда функция проходит через начало координат, 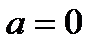 .
.
В этом случае поиск коэффициента b методом наименьших квадратов сводится к нахождению среднего арифметического значения всех коэффициентов преобразования в каждой точке контроля аппаратуры:
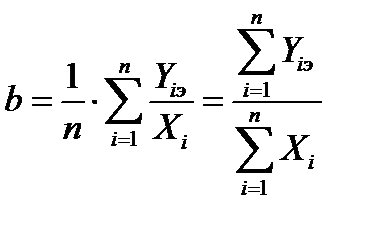 . (56)
. (56)
Для оценки погрешности СИ с построенной КФ необходимо найти отклонения экспериментальных точек от КФ с полученными коэффициентами a и b. Для этого в каждой i-той точке контроля необходимо по построенной КФ определить измеренное значение Yi-изм, по выходному сигналу Хi. Затем в каждой i-той точке контроля вычислить оценку поправки по формуле
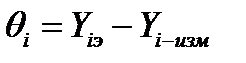 . (57)
. (57)
Для каждой точки контроля абсолютную погрешность 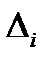 найдем как алгебраическую сумму модуля оценки поправки и допускаемой абсолютной погрешности i-того эталона
найдем как алгебраическую сумму модуля оценки поправки и допускаемой абсолютной погрешности i-того эталона 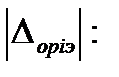

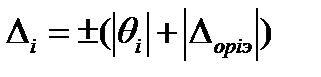 , (58)
, (58)
и либо выберем максимальную из них, либо построим зависимость оценки погрешности от измеряемого параметра.
Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры принимается максимальное значение, вычисленное во всех точках контроля с использованием вновь построенной КФ:
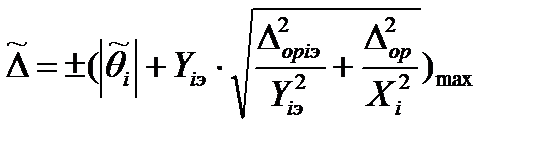 . (59)
. (59)
16.3 Способы построения параболической КФ вида 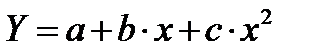
Алгебраический способ
Исходные данные: эталон воспроизводит только три значения измеряемого параметра  ,
, 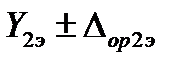 и
и 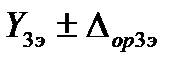 ; им соответствуют три измеренных значения выходного сигнала калибруемой аппаратуры
; им соответствуют три измеренных значения выходного сигнала калибруемой аппаратуры 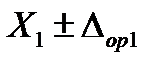 ,
, 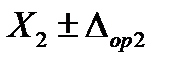 и
и 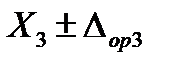 .
.
На основании таких исходных данных может быть составлена система трёх линейных уравнений с тремя неизвестными a, b и c в следующем виде:
 ;
;
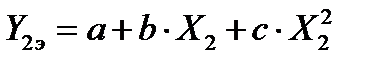 ; (60)
; (60)
 .
.
Эта система имеет однозначное алгебраическое решение:
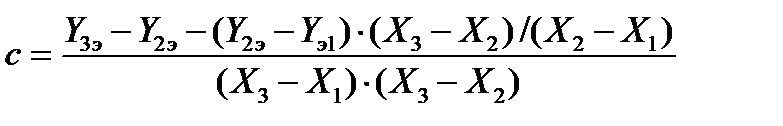 ;
;
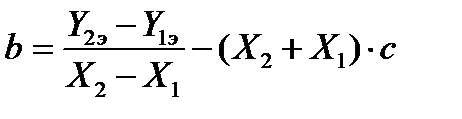 ; (61)
; (61)
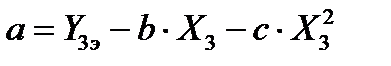 .
.
За оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается максимальная из допускаемых погрешностей эталонов (либо 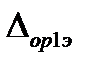 , либо
, либо 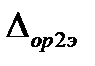 , либо
, либо 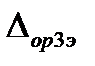 ).
).
Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры принимается максимальное из следующих значений:
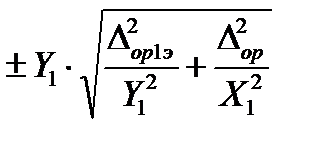 или
или 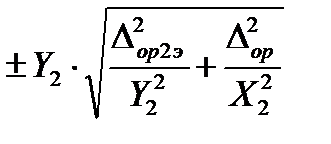 или
или 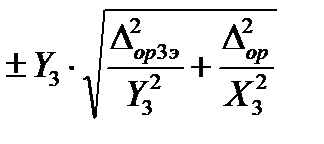 .
.
Статистический способ
Исходные данные: эталон воспроизводит более трёх значений измеряемого параметра, например, для n значений 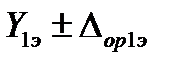 ,
, 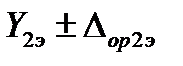 , … и
, … и 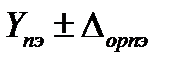 ; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры
; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры 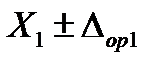 ,
, 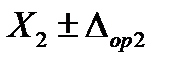 , … и
, … и  .
.
На основании таких исходных данных может быть составлена система n линейных уравнений с тремя неизвестными a, b и c в следующем виде:
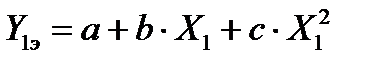 ;
;
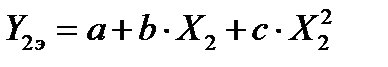 ; (62)
; (62)
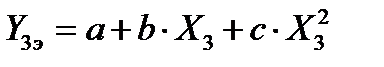 ;
;
…
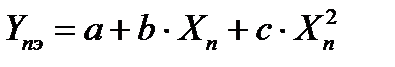 .
.
Эта система уравнений решается на основе метода наименьших квадратов. Из нее составляют систему из трех нормальных уравнений с тремя неизвестными a, b и c.
Нормальные уравнения получают по следующему правилу.
Первое нормальное уравнение получим в результате суммирования левой и правой частей системы (62) с последующим умножением обоих частей на сумму квадратов всех измеренных значений выходного сигнала Х.
Второе уравнение получим в результате суммирования левой и правой частей этой системы после умножения каждого уравнения на коэффициент при неизвестном b с последующим умножением обоих частей на сумму всех измеренных значений выходного сигнала Х.
Третье уравнение получим в результате суммирования левой и правой частей этой системы после умножения каждого уравнения на коэффициент при неизвестном с.
В итоге получим следующую новую систему трех уравнений с тремя неизвестными:
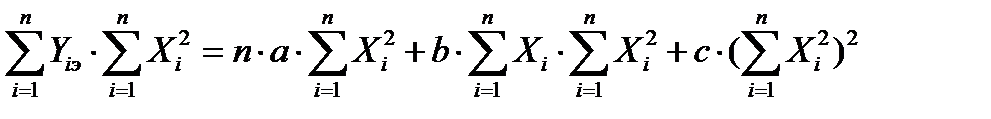 ;
;
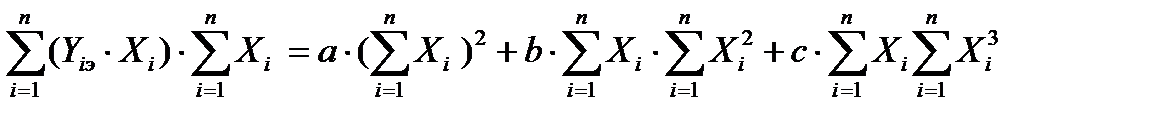 ; (63)
; (63)
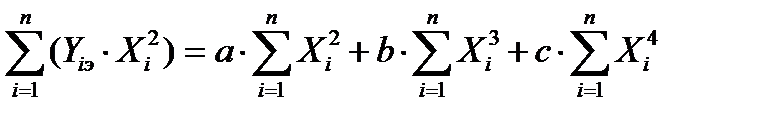 .
.
В результате ее решения найдем коэффициенты a, b и c параболической КФ 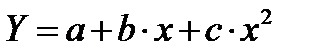 , вычисляемые по формулам:
, вычисляемые по формулам:
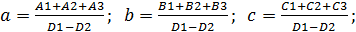 (64)
(64)
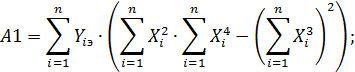

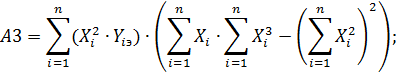
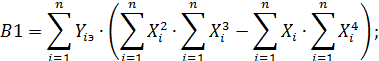
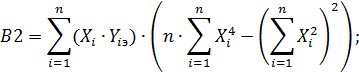
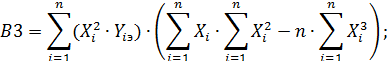

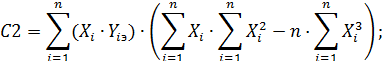
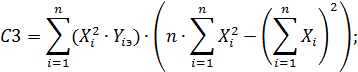
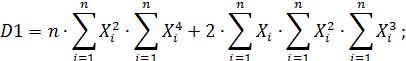
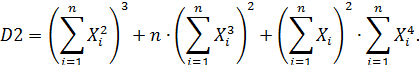
Если полученные коэффициенты a, b и c подставить в исходную систему (62), то получим совокупность измеренных значений Y1изм, Y2изм, Y3изм … и Yn-изм при тех же самых значениях выходных сигналов. Для каждого из них найдем оценку поправки по формуле (57).
В каждой точке контроля найдем оценку абсолютной погрешности как сумму модуля полученной оценки поправки и нормированной абсолютной погрешности эталона по формуле (58) и в качестве абсолютной погрешности аппаратуры выберем максимальную из них или построим зависимость оценки погрешности от измеряемого параметра.
Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры принимается максимальное значение, вычисленное во всех точках контроля по формуле (59).
Следует отметить, что количество эталонов, применяемых для калибровки геофизических средств измерений, редко может превысить четырех или пяти. Следовательно, в системе (62) будет такое же количество уравнений соответственно.
16.4 Способы построения логарифмической КФ вида 
Алгебраический способ
Исходные данные: эталон воспроизводит только два значения измеряемого параметра 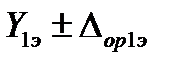 и
и 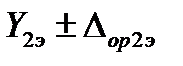 ; им соответствуют два измеренных значения выходного сигнала калибруемой аппаратуры
; им соответствуют два измеренных значения выходного сигнала калибруемой аппаратуры 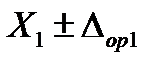 и
и 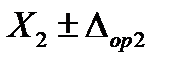 .
.
На основании таких исходных данных может быть составлена система двух уравнений с двумя неизвестными a и b в следующем виде:
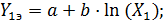
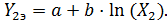 (65)
(65)
Найдем решение этой системы, исходя из предположения, что a = Y1э . Это возможно только в том случае, когда второе слагаемое в первом уравнении равно 0 при ln(1) = 0 после замены переменной Х на Х/Х1. Тогда b найдем из второго уравнения:
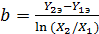 . (66)
. (66)
В итоге КФ имеет вид:
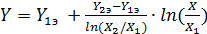 . (67)
. (67)
За оценку погрешности аппаратуры с вновь построенной логарифмической КФ принимается максимальная из нормированных погрешностей эталонов (либо, 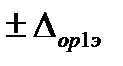 либо
либо 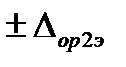 ), когда погрешностью измерений параметров выходного сигнала можно пренебречь.
), когда погрешностью измерений параметров выходного сигнала можно пренебречь.
Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры с вновь построенной КФ принимается максимальное из значений, вычисленных по формулам (58) и (59).
Статистический способ
Исходные данные: эталон воспроизводит более двух значений измеряемого параметра, например, для n значений 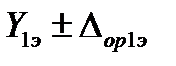 ,
, 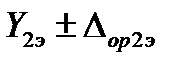 , … и
, … и 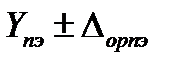 ; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры
; им соответствуют n измеренных значений выходного сигнала калибруемой аппаратуры 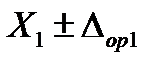 ,
, 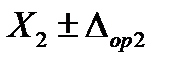 , … и
, … и  .
.
На основании таких исходных данных может быть составлена система n линейных уравнений с двумя неизвестными a и b в следующем виде:
 ;
;
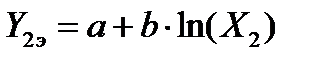 ; (68)
; (68)
…
 .
.
Найдем решение этой системы, исходя из предположения, что a = Y1э . Заменим переменную Х на Х/Х1. и приравняем суммы левой и правой частей системы. Из полученного уравнения найдем b как:
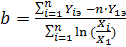 . (69)
. (69)
Для оценки погрешности калибровки СИ необходимо найти отклонения экспериментальных точек от построенной КФ с коэффициентами a и b. Для этого в каждой i-той точке контроля необходимо по построенной КФ определить измеренное значение Yизм,i при выходном сигнале Хi. Затем в каждой i-той точке контроля вычислить поправку по формуле:
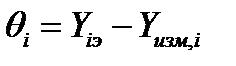 . (70)
. (70)
Для каждой точки контроля абсолютную погрешность 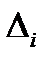 найдем как алгебраическую сумму модуля поправки и модуля нормированного предела абсолютной погрешности i-того эталона
найдем как алгебраическую сумму модуля поправки и модуля нормированного предела абсолютной погрешности i-того эталона 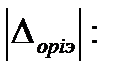

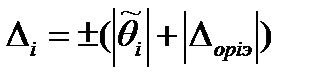 , (71)
, (71)
и либо выберем максимальную из них, либо построим зависимость оценки погрешности от измеряемого параметра.
Если погрешностью измерений параметров выходного сигнала пренебречь нельзя, то за оценку абсолютной погрешности аппаратуры принимается максимальное значение, вычисленное во всех точках контроля с использованием вновь построенной КФ, по формуле:
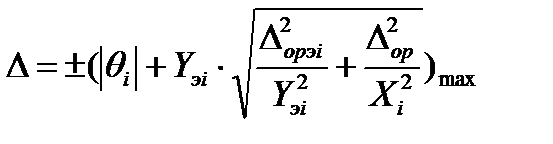 . (72)
. (72)
16.5 Способ построения линейной КПФ
вида 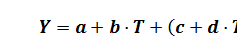
Предполагается, что зависимость изменения показаний Х от влияющей величины Т линейна на основании априорных данных. Тогда калибровочно-поправочную функцию можно представить в виде плоской поверхности  .
.
Исходные данные: эталон воспроизводит только два значения измеряемого параметра 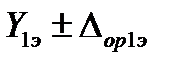 и
и 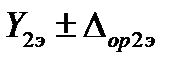 ; воспроизводятся два значения влияющего фактора
; воспроизводятся два значения влияющего фактора  и
и 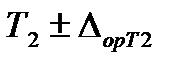 . Им соответствуют четыре измеренных значения выходного сигнала калибруемой аппаратуры
. Им соответствуют четыре измеренных значения выходного сигнала калибруемой аппаратуры  ;
; 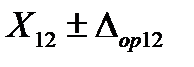 ;
; 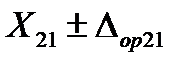 ;
; 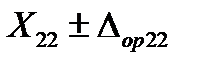 , где первый индекс соответствует номеру эталона, а второй номеру значения влияющего фактора.
, где первый индекс соответствует номеру эталона, а второй номеру значения влияющего фактора.
На основании таких исходных данных может быть составлена система четырех линейных уравнений с четырьмя неизвестными a, b, с и d в следующем виде:
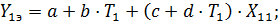
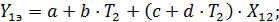
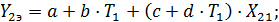
 (73)
(73)
Эта система имеет однозначное решение:
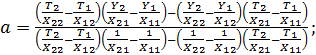 (74)
(74)
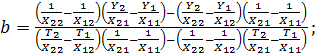 (75)
(75)
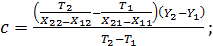 (76)
(76)
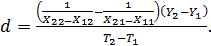 (77)
(77)
Если переменную Т заменить переменой Т-Т0, где Т0 – нормальное значение влияющего фактора, а коэффициенты а и с считать известными при Т0, то коэффициенты в и d найдем, решая систему уравнений:
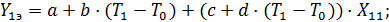
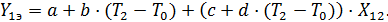
Выделив искомые коэффициенты в и d , система приобретает вид:
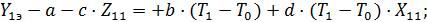
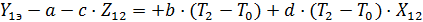 .
.
Откуда
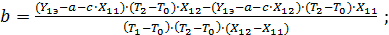 (78)
(78)
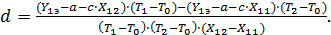 (79)
(79)
Обычно погрешностью измерений влияющего фактора и выходного сигнала можно пренебречь. Тогда за оценку погрешности аппаратуры с вновь построенной КПФ принимается максимальная из нормированных абсолютных погрешностей эталонов (либо, 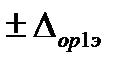 либо
либо 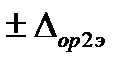 ).
).
Дата добавления: 2018-06-01; просмотров: 2230; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
