О свойствах произведений классов Локетта
Турковская А.В.,
студентка 5 курсаУО «ВГУ им. П.М. Машерова», г. Витебск, Республика Беларусь
Научный руководитель – Воробьев Н.Т., доктор физ.-мат. наук, профессор
Классом Фиттинга называется класс групп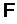 
, удовлетворяющий следующим требованиям:
1) каждая нормальная подгруппа группы из 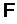также принадлежит ;
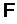2) из N1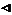 
G и N1 Î 
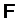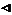, N2 G и N2 Î 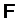всегда следует N1N2 Î .
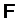Если 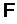непустой класс Фиттинга, то для любой группы 
существует наибольшая нормальная 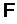‑подгруппа, которую называют 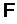‑радикалом.
Для описания свойств произведений классов Фиттинга [1] мы будем использовать оператор Локетта «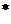 
» [2]. Напомним, что если 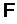– произвольный непустой класс Фиттинга, то 
– наименьший из классов Фиттинга содержащий 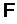, такой, что для любых групп G и H справедливо равенство 
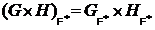[2]. Следует отметить, что классом Локетта называют класс Фиттинга 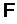такой, что 
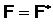[3, с.681]. В частности, класс Фиттинга является классом Локетта, так как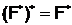 
[3, с. 679].
Нами получены свойства произведений классов Локетта, которые представляет следующая
Теорема. Пусть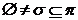 
, 
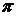– такое непустое множество простых чисел, что 
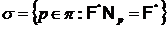, тогда:
1) 
;
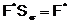2) если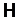 
– класс Фиттинга и L – группа минимального порядка в классе 
, то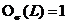 
.
Доказательство.Покажем, что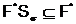 
.
Ввиду [4, c.190] 
.
Докажем, что 
. Предположим, что это не верно. Тогда существует группа Х, такая, что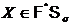 
и 
. Выберем среди таких групп группу G минимального порядка, то есть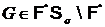 
. Пусть M – максимальная нормальная подгруппа группы G. Так как 
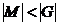и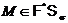 
, то по индукции получаем, что 
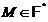и поэтому 
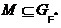. По предположению M – максимальная нормальная подгруппа группы G. Ввиду максимальности нормальной p‑подгруппы 
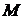и по определению 
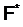‑радикала 
.
Рассмотрим факторгруппу G/M . Так как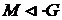 
, то G/M – главный фактор группы G. Заметим, что 
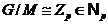[4, с. 48] и [4, с. 44]. По условию 
.Следовательно, по определению произведения классов Фиттинга получаем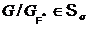 
. Итак, 
.
Если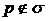 
, то 
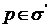. Значит, 
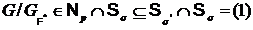. Следовательно, 
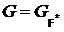и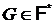 
. Последнее противоречит выбору группы G.
Если 
, то 
. Следовательно,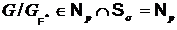 
. Следовательно, по определению произведения классов Фиттинга 
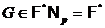. Получили противоречие с выбором группы G.
Полученные противоречия доказывают, что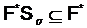 
.
Значит,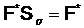 
и утверждение 1 доказано.
Докажем утверждение 2. Предположим, что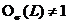 
. По условию 
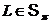. Рассмотрим факторгруппу 
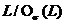, принадлежащую классу 
всех разрешимых p‑групп. Отметим, что 
. Следовательно, по индукции получаем, что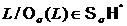 
. Так как 
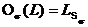, то 
. По определению произведения классов Фиттинга получаем 
. В виду ассоциативности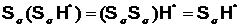 
. Значит, 
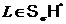. Последнее противоречит выбору группы L.
Полученное противоречие доказывает, что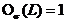 
.
Теорема доказана.
Литература:
1. Blessenohl, D. Über normale Schunk und Fittingklassen / D. Blessenohl, W. Gaschütz. – Math. Z. – Bd. 148, № 1, 1970. – S. 1–8.
2. Lockett, P. The Fitting class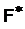 
/ P. Lockett. – Math. Z. 137, 1974.– 131‑136 p.
3. Doerk, K. Finite soluble groups/ K. Doerk, T. Hawkes. – Berlin; New York de Gruyter, 1992. – 893 p.
4. Монахов, С.В. Введение в теорию конечных групп и их классов / С.В. Монахов. – Мн.: Высшая школа, 2006. – 207с.
Дата добавления: 2018-05-09; просмотров: 220; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!