Елементи комбінаторики в теорії ймовірностей: переставлення, розміщення та комбінації

При розв’язуванні задач з теорії ймовірностей побудувати простір елементарних подій (множину W) можна не завжди.

Для більшості прикладних задач така побудова пов’язана з виконанням великого обсягу робіт, а нерідко й взагалі неможлива. Щоб обчислити ймовірність тієї чи іншої випадкової події для певного класу задач із дискретним і обмеженим простором елементарних подій, необхідно вміти обчислити кількість n усіх елементарних подій (елементів множини W) і число m елементарних подій, які сприяють появі випадкової події.

Існує клас задач, в яких для обчислення n і m використовуються елементи комбінаторики: переставлення, розміщення та комбінації. У комбінаториці оперують множинами однотипних елементів.

Загалом множини бувають упорядковані та невпорядковані.

Множину називають упорядкованою, якщо при її побудові істотним є порядок розміщення елементів.

У противному разі множину називають невпорядкованою.

Переставлення. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення.

Кількість таких упорядкованих множин обчислюється за формулою

, (3)

де n набуває лише цілих невід’ємних значень.

Оскільки 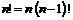, то при n = 1 маємо

1! = 0!

Отже, 0! = 1.

Розміщення. Розміщенням із n елементів по m (0 ) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом.

Кількість таких множин обчислюється за формулою

. (4)

Комбінації. Комбінаціями з n елементів по називаються такі множини з m елементів, які різняться між собою хоча б одним елементом.

Кількість таких множин

. (5)

Аксіоми теорії ймовірностей та їх наслідки

Загалом функції дійсних змінних бувають визначеними не на всій множині дійсних чисел, а лише на певній її підмножині, яку називають областю визначення функції.

Імовірність також не завжди можна визначити для будь-яких підмножин множини Ω (простору елементарних подій). Тому доводиться обмежуватися певним класом підмножин, до якого висуваються вимоги замкненості відносно операцій додавання, множення та віднімання.

Нехай задано довільний простір елементарних подій — множину Ω і Q — деяка система випадкових подій.

Система подій називається алгеброю подій, якщо:

1. Ώ Î Q.

2. Із того, що А Î Q, В Î Q, випливає: що А В Î Q , А В Î Q, А \ В Î Q.

Із тверджень 1 і 2 дістаємо, що Ø = Ώ \ Ώ, а отже, Ø Ì Q. Найменшою системою, яка буде алгеброю подій, є Q = (Ø, Ώ). Якщо Ώ — обмежена множина, то система Q також буде обмеженою. Якщо множина містить n елементів, то кількість усіх підмножин буде 2ⁿ.

Якщо Ω є неперервною множиною, то система Q утворюється квадровними підмножинами множини Ω, які також утворюють алгебру подій.

Числова функція Р, що визначена на системі подій Q, називається ймовірностю, якщо:

1. Q є алгеброю подій.

2. Для будь-якого А Ì Q існує .

3. Р (Ω) = 1.

4. Якщо А і В є несумісними (А В = Ø), то

. (6)

Для розв’язування задач з нескінченними послідовностями подій, наведені аксіоми необхідно доповнити аксіомою неперервності.

5. Для будь-якої спадної послідовності подій із Q, такої, що Ø, випливає рівність

Трійка (Q, Ω, Р), де Q є алгеброю подій і Р задовольняє аксіоми 1—5, називається простором імовірностей.

Наслідки аксіом

1. Якщо випадкові події А₁, А₂, А₃, … А_n є несумісними попарно, то

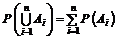. (7)

2. Якщо випадкові події А_1, А₂, А₃, … А_n утворюють повну групу, то

. (8)

Із рівності А = Ω і аксіом 3, 4 випливає, що

. (9)

Якщо Ø, то

. (10)

3. Формула додавання для n сумісних випадкових подій має такий вигляд:

(12)

Наприклад, для трьох сумісних випадкових подій формулу (12) можна записати так:

. (13)

4. Якщо випадкова подія А сприяє появі 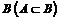, то

. (14)

6. Геометрична ймовірність

Класичне означення ймовірності придатне лише для експериментів з обмеженим числом рівномірних елементарних подій, тобто коли множина Ώ (простір елементарних подій) обмежена.

Якщо множина Ώ є неперервною і квадровною, то для обчислення ймовірності А (А Ì Ώ) використовується геометрична ймовірність

. (15)

Якщо множина Ώ вимірюється в лінійних одиницях, то Р (А) дорівнюватиме відношенню довжини, якщо Ώ вимірюється у квадратних одиницях, то Р (А) дорівнюватиме відношенню площ, і т. ін.

Статистична ймовірність

На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій (множини Ώ). Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність.

Насамперед уводиться поняття відносної частоти випадкової події W (A).

Відносною частотою випадкової події А W(A) називається відношення кількості експериментів m, при яких подія А спостерігалася, до загальної кількості n проведених експериментів:

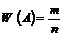. (16)

Як і для ймовірності випадкової події, для відносної частоти виконується нерівність

Теорія ймовірностей вивчає лише такі випадкові події, в яких спостерігається стабільність відносних частот, а саме: у разі проведення k серій експериментів існує така константа Р(А), навколо якої групуватимуться відносні частоти досліджуваної випадкової події А, тобто W_і (А). І це групування буде тим ближчим до цієї константи, чим більшим буде число n експериментів.

На рис. 6 показано, як W_і (А) змінюється зі збільшенням n експериментів.

Рис. 6

Імовірність випадкової події визначається так: упевнившись, що існує стабільність відносних частот випадкової події W_і (А), задаємось малим додатним числом e і проводимо серії експериментів, збільшуючи їх число n. Якщо на якомусь кроці серії експериментів виконуватиметься нерівність 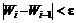, то за ймовірність випадкової події береться одне з чисел W_і або W_і _{– 1}. Ця ймовірність називається статистичною.

Дата добавления: 2018-05-09; просмотров: 170; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!