Характеристика линейной оптимизационной модели. Примеры задач линейного программирования и графический метод их решения.
С классом детерминированных моделей мы начинаем знакомство с помощью моделей линейного программирования. Для описания таких моделей используются линейные функции. Разумеется, реальные зависимости между экономическими переменными, как правило, являются нелинейными. Однако на практике допущение о линейности используется весьма часто.
Познакомимся с характерными примерами линейных моделей оптимизации.
Задача определения оптимальной производственной программы.
Предприятие выпускает nвидов продуктов, используя m видов ресурсов, запасы которых в рассматриваемом периоде изменить нельзя.
Известны:
- цены продажи изделий 
;
- запасы ресурсов 
;
- нормы расхода ресурсов на выпуск единицы изделия 
.
Требуется: определить объемы выпуска изделий, обеспечивающие предприятию максимум выручки.
Введем в модель задачи вектор х, компоненты которого 
обозначают объемы выпуска изделий. В таком случае целевая функция задачи будет иметь следующий вид:
.
Для построения ограничений задачи воспользуемся таблицей коэффициентов 
(табл. 1) и обозначениями показателей запасов ресурсов .
Таблица 1. Нормы расхода ресурсов ( коэффициенты )
| Продукт 1 | Продукт 2 | …. | Продукт n | |
| Ресурс 1 | 
| 
| …. | 
|
| Ресурс 2 | 
| 
| ….. | 
|
| . . . | . . . | . . . | . . . | . . . |
| Ресурс m | 
| 
| …… | 
|
Ограничения по ресурсам:
|
|
|
Модель задачи можно представить в виде краткой формы записи:
при ограничениях 
.
Рассмотренная выше задача имеет симметричную форму записи, для которой характерно одновременное соблюдение трех признаков: 1) целевая функция максимизируется; 2) все ограничения являются неравенствами со знаком « 
»; 3) все переменные имеют неотрицательное значение. Такая разновидность симметричной записи именуется симметричной на максимум целевой функции. Далее будет рассмотрена задача, которая также имеет симметричную запись, но в другом ее варианте.
Задача определения оптимального состава технологической смеси.
Смесь включает m компонентов. Для ее изготовления доступны n продуктов. Содержание компонентов не может быть ниже установленного минимума.
Известны:
- цены продуктов 
;
- показатели минимально допустимого содержания компонентов 
;
- показатели концентрации компонентов в продуктах 
.
Требуется составить смесь минимальной стоимости.
Введем в модель задачи вектор x, компоненты которого 
обозначают количества продуктов для составления смеси. В таком случае формула
целевой функции (стоимость смеси) примет следующий вид:
.
Для построения ограничений воспользуемся таблицей коэффициентов (табл. 2) и обозначениями показателей минимально допустимого содержания компонентов .
|
|
|
Таблица 2. Показатели концентрации компонентов в продуктах (коэффициенты ).
| Продукт 1 | Продукт 2 | …. | Продукт n | |
| Компонент 1 | 
| 
| …. | 
|
| Компонент 2 | 
| 
| ….. | 
|
| . . . | . . . | . . . | . . . | . . . |
| Компонент m | 
| 
| …… | 
|
Ограничения по компонентам:
Данная задача, как и задача определения оптимальной производственной программы, также имеет симметричную запись, однако другую ее разновидность – симметричную на минимум целевой функции. Для такой разновидности записи характерно одновременное выполнение трех требований: 1) целевая функция минимизируется; 2) все ограничения являются неравенствами со знаком « 
»; 3) все переменные имеют неотрицательное значение.
Транспортная задача.
В распоряжении m грузоотправителей имеется некоторый запас однородного груза, который необходимо доставить n грузополучателям, в соответствии с объемами их потребностей.
Известны:
- тарифы ( ден. ед.) на доставку единицы груза 
;
- показатели запасов груза ( физ ед.) 
;
- показатели потребностей в грузе (физ. ед.) 
.
|
|
|
Требуется: составить план перевозок груза, минимизирующий суммарные затраты на доставку его потребителям.
В таблице 3 отражены исходные данные задачи. Предваряя составление модели, следует заметить, что в отличие от ранее рассмотренных задач, в транспортной задаче ограничения являются равенствами. Это объясняется тем, что суммарный запас груза в точности совпадает с суммарной потребностью в нем.
Таблица 3. Тарифы на доставку единицы груза 
и прочие исходные данные.
| Получатель 1 | Получатель 2 | …………. | Получатель n | Запас груза | |
| Отправитель 1 | 
| 
| ………….. | 
| 
|
| Отправитель 2 | 
| 
| …………. | 
| 
|
| . . . | . . . | . . . | . . . | . . . | |
| Отправитель m | 
| 
| …………. | 
| 
|
| Потребность в грузе | 
| 
| ………….. | 
|
Пусть переменные задачи 
обозначают количество груза, доставляемого i-тым отправителем j-тому получателю.
Формула целевой функции:
.
Ограничения:
Транспортная задача имеет каноническую форму записи. В канонической записи должны одновременно соблюдаться два требования: 1) все ограничения являются равенствами; 2) все переменные имеют неотрицательное значение. В дополнение следует заметить, что запись с нарушением требований симметричной или канонической форм называется общей.
|
|
|
Рассмотрим несложный пример задачи линейного программирования с двумя инструментальными переменными. Такую задачу можно решить графическим методом. Стоит напомнить, что графический метод можно применить во всех случаях, когда запись модели задачи можно представить так, что она будет содержать не более двух инструментальных переменных.
Пример ЗЛП.
Предприятие выпускает изделия двух видов. Цена реализации изделия первого вида равна 4 ден. ед., а изделия второго вида - 6 ден. ед. Для изготовления изделий предприятие использует два вида ресурсов, запасы которых составляют, соответственно, 18 и 12 физ. ед. В рассматриваемом периоде запасы ресурсов изменению не подлежат. Установлены нормы расхода ресурсов на выпуск единицы изделия каждого вида (см. таблицу исходных данных). Анализ состояния спроса показал, что емкость рынка для первого изделия составляет 12 физ. ед., а для второго – 9 физ. ед. Необходимо определить план выпуска изделий, максимизирующий валовой доход (выручку) предприятия.
Таблица 4. Исходные данные задачи.
|
| Нормы расхода ресурсов на единицу изделия, физ. ед. | Запас ресурса, физ.ед. | |
| Для продукта 1 | Для продукта 2 | ||
| Ресурс 1 | 1 | 1 | 18 |
| Ресурс 2 | 0,5 | 1 | 12 |
| Емкость рынка, физ.ед. | 12 | 9 | |
| Цена единицы изделия, ден. ед. | 4 | 6 | |
Математическая модель задачи:
при ограничениях
Данная задача может быть решена графическим методом.
На рис. 1 приведено графическое решение задачи.
Примечания.
А) Для построения ОДР использованы следующие обозначения линий ограничений:
(1)
(2)
(3)
(4)
Б) Для построения линий уровня Z использовался кратный градиенту 
вектор l=(12;18).
|
|
|
|
|
|
|
Рис.1. Графическое решение задачи
Симплекс-метод
Возможность использовать графический метод решения задач линейного программирования возникает редко. Как правило, размерность модели такова, что ее запись нельзя трансформировать с сохранением одной или двух инструментальных переменных. Симплекс-метод является универсальным способом решения задач линейного программирования любой размерности.
Подготовка задачи к применению симплекс-метода включает две процедуры: 1) трансформацию записи задачи из общей или симметричной в каноническую (когда это необходимо); 2) определение начального неотрицательного базисного решения.
Приведем к каноническому виду задачу определения оптимальной производственной программы, записанную в симметричной форме. Воспользуемся неотрицательными балансовыми переменными, которые добавим к левым частям ограничений-неравенств. В целевую функцию данные переменные вводятся с нулевыми коэффициентами. Таким образом, запись задачи примет следующий вид:
Убедимся в том, что мы располагаем неотрицательным базисным решением. Признак наличия такого решения следующий: в каждом уравнении системы ограничений должна присутствовать такая переменная, которая в данном уравнении имеет коэффициент 1, а в остальных уравнениях системы коэффициент 0. Таким образом, в матрице системы при соответствующем размещении столбцов должна выделяться единичная подматрица.
Если система данному требованию не соответствует, то существует две альтернативных возможности получения неотрицательного базисного решения: 1) преобразование матрицы методом полного исключения переменных; 2) введение в модель искусственных переменных с соответствующим изменением записи.
В рассматриваемом примере матрица системы удовлетворяет сформулированному выше требованию, поскольку единичная подматрица формируется коэффициентами балансовых переменных.
Для объяснения процедуры использования симплекс-метода важно напомнить понятие базисной переменной и базисного решения. Базисными именуются все те переменные, коэффициенты которых образуют столбцы единичной подматрицы. Остальные переменные будем именовать свободными. Если выразить базисные переменные через свободные, а свободные переменные приравнять к нулю, то мы получим базисное решение системы линейных уравнений.
Убедившись в наличии неотрицательного базисного решения, можно приступать к реализации процедуры симплекс-метода. Рассмотрим табличную форму записи хода решения.
Заполняем симплексную таблицу, предварительно приведя задачу к каноническому виду и выделив начальное неотрицательное базисное решение. Переменные 
являются свободными, а переменные 
-базисными.
Таблица 5 иллюстрирует один из существующих стандартов заполнения симплексных таблиц.
Таблица 5. Исходная симплексная таблица.
| БП | Сб | Ао | 
|  . . .
| 
| 
|  . . .
| 
|
|  . . .
| 
| 0 | 0 | 0 | |||
|
| 0 | 
| 
|  . . .
| 
| 1 | 0 | 0 |
|
| 0 | 
| 
|  …
| 
| 0 | 1 | 0 |
| . . . | . . . | . . . | . . . | |||||
|
| 0 | 
| 
|  …
| 
| 0 | 0 | 1 |
| ∆ 0 | ∆1 | ∆2… | ∆n | 0 | 0 | 0 |
В данной таблице: БП – совокупность
базисных переменных; Сб – вектор коэффициентов, стоящих в целевой функции при базисных переменных; 
– коэффициенты при переменных в целевой функции; 
– вектор свободных членов ограничений;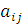 
– коэффициенты при переменных в системе уравнений; 
- значение целевой функции при начальном базисном решении; 
– оценки свободных переменных.
Для расчета – используем формулу 
. Оценки рассчитываем по формулам 
,
где 
- вектор коэффициентов при соответствующей переменной.
Процедура начинается с анализа заключительной строки таблицы, именуемой индексной (строкой оценок 
). Если в данной строке при решении задачи на максимум целевой функции все 
, а при решении на min все 
, то начальное базисное решение и является оптимальным.
Если существуют 
, не удовлетворяющие данному требованию, то необходимо продолжить поиск оптимального решения. Среди отрицательных 
при решении задачи на максимум (среди положительных при решении на min) выбираем наибольшую по модулю. В соответствующем ей столбце 
среди положительных коэффициентов 
выделяем разрешающий элемент, для которого отношение 
является минимальным.
Приступаем к заполнению следующей таблицы. Начинаем с определения нового состава БП. Поскольку количество базисных переменных постоянно, то место переменной 
займет та переменная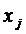 
, в столбце которой выбран разрешающий элемент. Затем определяем состав компонентов вектора 
и переносим без изменений столбцы 
тех переменных, которые остались базисными. На месте разрешающего элемента ставим 1, на остальных местах в данном столбце ставим 0, а остальные места в данной строке заполняем числами, полученными путем деления прежних чисел на разрешающий элемент.
Остальные элементы новой таблицы, включая свободные члены и оценки 
, получаем путем расчетов по так называемому правилу прямоугольника.
Пусть, например, в качестве разрешающего выбран элемент 
. Для вычисления элемента 
новой таблицы применяем следующую процедуру :
. На рисунке 2 представлена иллюстрация использования данного принципа.
 |
|
|
|
|
Рис. 2. Правило прямоугольника.
Иными словами, выделяем в исходной таблице прямоугольник, образованный пересечением разрешающих строки и столбца, а также строки и столбца элемента, подлежащего пересчету. Из произведения элементов основной диагонали, включающей разрешающий элемент, вычитаем произведение элементов второстепенной диагонали. Данную разность делим на разрешающий элемент.
После проведения расчетов можно осуществить проверку по формулам для вычисления 
и .
Если в результате преобразований все оценки индексной строки оказались неотрицательны при решении на max (или неположительны при решении на min), то оптимальное решение получено. В противном случае процедура повторяется.
Ответ задачи состоит из оптимальных значений переменных 
и экстремального значения Z. Экстремум целевой функции размещен в ячейке 
, оптимальные значения базисных переменных находятся в столбце 
, значения свободных переменных равны нулю.
Искусственный базис формируется (в тех случаях, когда это необходимо и целесообразно) коэффициентами неотрицательных переменных 
, которые добавляются к левым частям уравнений, образующих систему ограничений задачи. В целевую функцию эти переменные включаются с коэффициентом «-М» при решении задачи на максимум и «+М» при решении задачи на минимум целевой функции. «М» символизирует бесконечно большое положительное число.
Задача с искусственными переменными решается симплекс-методом в соответствии с описанной выше процедурой. Первоначальный базис формируется столбцами коэффициентов искусственных переменных. По мере перехода к последующим таблицам, искусственные переменные вытесняются из числа базисных. Если искусственная переменная исключается из состава базисных, то в следующей таблице ее столбец просто ликвидируют.
Оптимальное решение М-задачи (если оно существует) является также и оптимальным решением исходной задачи.
В таблицах 6-9 проиллюстрирован ход решения задачи определения оптимальной производственной программы, рассмотренной в подразделе 2.1.
В результате трансформации записи задачи из симметричной в каноническую автоматически выделяется базис системы уравнений. Это дает возможность заполнить первую симплексную таблицу (табл. 6).
Таблица 6. Первая симплексная таблица.
| БП | Сб | Ао | X1 | X2 | X3 | Х4 | X5 | X6 |
| 4 | 6 | 0 | 0 | 0 | 0 | |||
| X3 | 0 | 18 | 1 | 1 | 1 | 0 | 0 | 0 |
| X4 | 0 | 12 | 0,5 | 1 | 0 | 1 | 0 | 0 |
| Х5 | 0 | 12 | 1 | 0 | 0 | 0 | 1 | 0 |
| X6 | 0 | 9 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | -4 | -6 | 0 | 0 | 0 | 0 | ||
Проверка индексной строки показывает, что оптимум не достигнут. Следовательно, решение следует продолжить. Определяем разрешающий элемент. В таблице его местоположение отмечено пересечением выделенных строки и столбца. Выбор разрешающего элемента позволяет заполнить следующую таблицу (табл.7).
На первом этапе решения значение целевой функции равно нулю. Переход к новому базисному решению должен увеличить значение Z.
Таблица 7. Вторая симплексная таблица.
| БП | Сб | Ао | X1 | X2 | X3 | Х4 | X5 | X6 |
| 4 | 6 | 0 | 0 | 0 | 0 | |||
| X3 | 0 | 9 | 1 | 0 | 1 | 0 | 0 | -1 |
| X4 | 0 | 3 | 0,5 | 0 | 0 | 1 | 0 | -1 |
| Х5 | 0 | 12 | 1 | 0 | 0 | 0 | 1 | 0 |
| X2 | 6 | 9 | 0 | 1 | 0 | 0 | 0 | 1 |
| 54 | -4 | 0 | 0 | 0 | 0 | 6 | ||
Новое базисное решение увеличило значение Z до 54, однако оптимум вновь не достигнут. Решение следует продолжить.
После выбора разрешающего элемента заполняем следующую таблицу (табл. 8).
Таблица 8. Третья симплексная таблица.
| БП | Сб | Ао | X1 | X2 | X3 | Х4 | X5 | X6 |
| 4 | 6 | 0 | 0 | 0 | 0 | |||
| X3 | 0 | 3 | 0 | 0 | 1 | -2 | 0 | 1 |
| X1 | 4 | 6 | 1 | 0 | 0 | 2 | 0 | -2 |
| Х5 | 0 | 6 | 0 | 0 | 0 | -2 | 1 | 2 |
| X2 | 6 | 9 | 0 | 1 | 0 | 0 | 0 | 1 |
| 78 | 0 | 0 | 0 | 8 | 0 | -2 | ||
Значение Z увеличилось до 78, но максимум целевой функции не достигнут. Поиск оптимального решения следует продолжить.
Заполняем очередную таблицу (табл. 9).
Таблица 9. Заключительная симплексная таблица.
| БП | Сб | Ао | X1 | X2 | X3 | Х4 | X5 | X6 |
| 4 | 6 | 0 | 0 | 0 | 0 | |||
| X6 | 0 | 3 | 0 | 0 | 1 | -2 | 0 | 1 |
| X1 | 4 | 12 | 1 | 0 | 2 | -2 | 0 | 0 |
| Х5 | 0 | 0 | 0 | 0 | -2 | 2 | 1 | 0 |
| X2 | 6 | 6 | 0 | 1 | -1 | 2 | 0 | 0 |
| 84 | 0 | 0 | 2 | 4 | 0 | 0 | ||
В индексной строке нет отрицательных показателей. Следовательно, целевая функция достигла максимума, а полученное на данном шаге базисное решение является оптимальным.
Дата добавления: 2018-05-02; просмотров: 685; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!