Нелинейный корреляционный и регрессионный анализы
Корреляционное отношение. Критерии нелинейности связи
При нелинейной корреляционной связи равномерным изменениям одного признака соответствуют в среднем неравномерные, но подчиняющиеся определенной закономерности изменения другого признака. Нелинейная связь возникает обычно при заметном отклонении одного или обоих распределений признаков от нормального.
Линейную и нелинейную зависимость измеряет корреляционное отношение h=r, но чем сильнее выражена нелинейность связи, тем больше значение корреляционного отношения превышает величину коэффициента корреляции r. Способ расчета корреляционного отношения связан с техникой регрессионного анализа. В отличие от коэффициента корреляции, являющегося мерой обоюдной связи между признаками, корреляционное отношение способно отражать как зависимость признака у от признака х (hу/х), так и зависимость признака х от признака у (hх/у). Таким образом, для пары признаков могут быть рассчитаны два корреляционных отношения, первое из которых условно назовем прямым, а второе – обратным. В общем случае прямое и обратное корреляционные отношения не совпадают, но чем сильнее связь и чем ближе она к линейной, тем больше (вплоть до полного совпадения) сближаются между собой их значения. На практике, исходя из биологической значимости того или иного признака, рассчитывают обычно одно из двух корреляционных отношений.
|
|
|
Другое отличие от коэффициента корреляции состоит в том, что корреляционное отношение принимает значения не от –1 до +1, а от 0 до +1.
Корреляционное отношение – это отношение двух средних квадратичных отклонений, одно из которых характеризует часть изменчивости первого признака, обусловленную его зависимостью от второго признака, а второе является обычной мерой общей изменчивости первого признака:
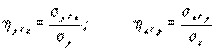, (4.37)
Для оценки достоверности корреляционного отношения необходимо вычислить ошибку квадрата этого показателя по формуле
(4.38)
где k – число классов вариационного ряда; n – объем выборки.
После этого можно использовать критерий Фишера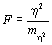 
сn1=k-1 иn2=n-k степенями свободы, сравнивая его со стандартным значением.
Рассмотрим конкретный пример. Изучается зависимость между высотой растения и числом пар цветков в осевом соцветии. Данные в виде корреляционной решетки приведены в табл. 4.6.
Точки эмпирических линий регрессии рассчитываются как взвешенные средние арифметические по строкам и столбцам. Для дальнейших расчетов необходимо знать средние арифметические и средние квадратичные отклонения обоих рядов. В рассматриваемом примере Му=134,7, sу=56, Мх= 7,8, sх=4,4. Расчеты ведутся в табличной форме в соответствии с алгоритмом, содержащимся в заголовках столбцов (табл. 4.7).
|
|
|
Таблица 4.6 – Корреляция между высотой растения (у) и числом пар цветков в осевом соцветии (х) у Odontites serotina Dum
| Х У | 2,5 | 6,5 | 10,5 | 14,5 | 18,5 | 22,5 | fy | X/y |
| 49,5 89,5 129,5 169,5 209,5 249,5 289,5 | 48 58 12 2 3 1 | 2 53 52 16 11 1 2 | 4 54 42 12 8 2 | 5 21 18 9 | 2 7 3 1 | 1 | 50 115 123 83 51 22 6 | 2,66 4,62 8,19 10,74 11,68 12,68 12,50 |
| fx | 124 | 137 | 122 | 53 | 13 | 1 | N=450 | |
| Y/x | 83,37 | 127,16 | 160,32 | 192,9 | 218,73 | 289,5 |
Величиной, характеризующей долю изменчивости признака у, обусловленную его зависимостью от признака х, будет сигма ряда взвешенных квадратов отклонений точек эмпирической линии регрессии у/х от Му:
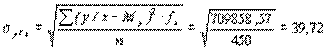(4.39)
Таблица 4.7 – Расчет прямого корреляционного отношения (hу/х) по данным табл.4.6
| х | У/х | У/х-Му | (у/х-Му)2 | fx | (y/x-My)2*fx |
| 2,5 6,5 10,5 14,5 18,5 22,5 | 83,37 127,16 160,32 192,9 218,73 289,5 | -51,33 -7,54 25,62 58,2 84,03 154,8 | 26,3477 56,85 656,38 3387,24 7061,04 23963,04 | 124 137 122 53 13 1 | 326711,48 7788,45 80078,36 179523,72 91793,52 23963,04 |
Му=134,7, sу=56, n=450 S=709858,57
Искомое корреляционное отношение составляет
.
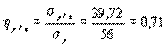Ошибка квадрата этого показателя
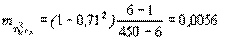, (4.40)
откуда F=0,712/0,0056=90,02.
|
|
|
Из таблицы критических значений критерия Фишера находим, что при n1=6-1=5 и n2=450-6=444 стандартное значение F01=3,06 и поскольку F>>Fst, полученное корреляционное отношение в высшей степени достоверно.
Аналогичным способом рассчитывается и обратное корреляционное отношение (hх/у), только теперь в основу расчетов берутся отклонения точек эмпирической линии регрессии х/у от Мх (табл. 4.8).
Таблица 4.8.– Расчет обратного корреляционного отношения (hх/у)по данным табл. 4.6
| у | Х/у | Х/у-Мх | (х/у-Мх)2 | fy | (x/y-Mx)2*fy |
| 49,5 89,5 129,5 169,5 209,5 249,5 289,5 | 2,66 4,62 8,19 10,74 11,68 12,68 12,5 | -5,14 -3,18 0,39 2,94 3,88 4,88 4,7 | 26,42 10,11 0,15 8,64 15,05 23,81 22,09 | 50 115 123 83 51 22 6 | 1321,0 1162,65 18,45 717,12 767,55 523,82 132,54 |
Мх= 7,8, sх=4,4 n=450 S=4643,13
Последовательно получаем:
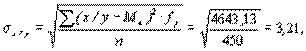
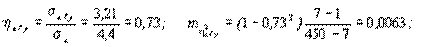
и при n1=7-1=6 и n2=450-7=443 стандартное значение F01=2,85 и поскольку F>>Fst, полученное корреляционное отношение в высшей степени достоверно. Как видно, прямое и обратное корреляционные отношения практически совпадают. Для сравнения, рассчитанный коэффициент корреляции равен 0,7, т.е. незначительно уступает по своей величине корреляционным отношениям. Это обстоятельство свидетельствует о том, что в рассмотренном примере корреляционная связь между признаками близка к линейной. Проверим это другим способом, более строгим, с помощью критерия нелинейности связи. Точно линейная связь в биологии такая же редкость, как и строго нормальное распределение признака. На практике небольшие отклонения связи от линейной можно не принимать в расчет и использовать линейные методы, облегчающие исследование корреляции и регрессии. Важно, однако, не переступить тот порог, по достижении которого отклонения связи от линейной становится существенным.
|
|
|
Известно несколько критериев нелинейности связи, в том или ином виде использующих разность h2-r2, т.е. требующих предварительного расчета корреляционного отношения и коэффициента корреляции и основанных на их сравнении. Наиболее часто употребляемыми являются критерий Блэкмана и критерий Фишера. Критерий Блэкмана проще:
n(h2-r2) >>11,37, (4.41)
где n – объем выборки; h – большее из двух корреляционных отношений; r – коэффициент корреляции. Связь признается нелинейной, если рассчитанное значение критерия превышает величину 11,37.
Критерий Фишера считается более точным:
, (4.42)
где kx – число классов в ряду х (если расчет ведется для прямого корреляционного отношения hу/х). Рассчитанное значение F сравнивается по обычным правилам со стандартным при числе степеней свободы n1=kx-2 и n2=n-kx. В рассматриваемом примере были получены значения hх/у=0,73; r=0,7 при n=450 и ky=7. Критерий Блэкмана, равный 19,31 превышает величину 11,37, что указывает на нелинейный характер зависимости. Критерий Фишера для данного корреляционного отношения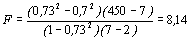 
подтверждает этот вывод, т.к. при степенях свободы n1=7-2=5 и n2=450-7=443 стандартное значение F01=3,06, т.е. F>Fst.
Этого достаточно для признания существенности нелинейности связи, т.к. расчет строится на большем из двух корреляционных отношений. Если же использовать меньшее из них (hу/х=0,71, к=6), то критерий Блэкмана 450(0,712-0,72)=6,3 позволяет считать связь линейной, а значение критерия ФишераF=3,16 при степенях свободыn1=4 иn2=444 лежит между стандартными значениями F05=2,39 и F01=3,36, т.е. в зависимости от нашей требовательности связь может быть признана линейной или нелинейной. В целом следует сделать вывод, что в рассматриваемом примере нелинейность связи незначительна.
Нелинейная регрессия
Когда одинаковым приращениям одного признака сопутствуют неодинаковые, но изменяющиеся по определенному закону приращения другого признака, регрессия, так же как корреляция, оказывается нелинейной. Внешним признаком нелинейной регрессии служит то, что эмпирические линии регрессии на графике выглядят кривыми различной конфигурации. При небольших отклонениях от линейности допустимо использование более простых приемов линейной регрессии, но в сомнительных случаях необходима проверка линейности связи.
Для интерполирования нелинейной регрессии используются различные способы. Одним из них является параболическое интерполирование. Уравнение параболы п-й степени y=a+bx+cx2+dx3+…+mxn представляет собой очень гибкую и удобную для расчетов функцию, широко используемую для интерполяции эмпирических данных. Ее можно «оборвать» на любом члене и получить последовательно выражения: у=а (отсутствие зависимости), y=a+bx (уравнение линейной зависимости),y=a+bx+cx2 (парабола второй степени) и т.д. Если имеется п точек, то парабола п-й степени имеет п-1 перегибов: при этом концы кривой уходят в бесконечность при четном п в одну сторону, при нечетномпв разные стороны.
Наращивая число членов уравнения (используя при п точках параболу степени п-1), в принципе можно описать почти все случаи нелинейной регрессии (т.е. добиться совпадения теоретической линии регрессии с эмпирическими точками). Вычисление парабол высоких степеней сопровождается резким увеличением громоздкости расчетов, но еще хуже то, что полученные при этом уравнения чаще всего не поддаются биологической интерпретации: имеет место лишь формальная «подгонка» эмпирических данных под достаточно гибкую математическую функцию.
Критерием правильности выбора функции может служить только удовлетворительное биологическое истолкование полученного результата. Если функция выбрана правильно и соответствует биологической сути описываемой зависимости, то она должна не только хорошо интерполировать эмпирические данные, но и допускать экстраполяцию за пределы наблюдаемого ряда. Добиться удовлетворительной экстраполяции удается далеко не всегда. Но нельзя выдавать интерполяционную формулу, хорошо выравнивающую эмпирический ряд, за модель всего биологического явления в целом. Следует отметить, что нужно стремиться подбирать функции с наименьшим числом параметров, как правило, с двумя или тремя, что позволяет их интерпретировать.
Общая схема расчета едина для парабол любой степени. Параболы степени выше третьей практически используются редко.
Обратимся к уравнению параболы второй степени y=a+bx+cx2, используя данные прежнего примера (табл. 4.3) регрессии длины на ширину листа у M. polonicum. Уже говорилось, что уравнение прямой (т.е. парабола первой степени) довольно хорошо интерполирует эту зависимость, но не допускает экстраполяцию в меньшую сторону (при ширине листа, равной нулю, его длина оказывается равной 18,92 мм).
Использование параболы второй степени.Расчет ведется методом наименьших квадратов, но в отличие от линейной регрессии придется решать систему не из двух, а уже из трех нормальных уравнений с тремя (a,b,c) неизвестными:
(4.43)
Как видно, по сравнению с уравнением прямой линии задача усложняется нахождением сумм ∑х3, ∑х4 и ∑х2 у. Расчет нужных сумм показан в левой части табл. 4.9.
Исходя из данных этой таблицы, составим систему нормальных уравнений:
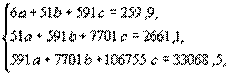
решая которую обычным алгебраическим путем, находим: с=-0,04; b=3,55; a=17,07.
Следовательно, уравнение параболы второй степени выглядит так: у=17,07+3,55х-0,04х2.
Таблица 4.9.– Выравнивание эмпирической линии регрессии длины листа (у)на его ширину (х) уMelampyrum polonicum (Beauv.) Soo уравнениемпараболы второй степени
| Расчеты для определения параметров уравнения | Построение теоретической линии регрессии | Расчет критерия χ2 | ||||||
| х3 | у4 | х2у | bх | cx2 | a+bx+cx2=y’ | y-y’ | (y-y’)2 | 
|
| 1 64 | 1 256 | 19,5 483,2 | 3,55 14,2 | -0,04 -0,64 | 20,58 30,63 | -1,08 -0,43 | 1,1664 0,1849 | 0,0567 0,006 |
| 343 1000 2197 4096 | 2401 10000 28561 65536 | 2048,2 5150,0 8855,6 16512 | 24,85 35,5 46,15 56,8 | -1,96 -4,0 -6,76 -10,24 | 39,96 48,57 56,46 63,63 | 1,84 2,93 -4,06 0,87 | 3,3856 8,5849 16,4836 0,7569 | 0,0847 0,1768 0,292 0,0119 |
| 7701 | 106755 | 33068,5 | - | - | 259,83 | 0,07 | 30,5623 | 0,6281 |
Примечание. Значения х,у,ху,х2 см. в табл. 4.5.
Путем обратного вычисления (табл. 4.9) можно рассчитать точки (y’) теоретической линии регрессии и построить соответствующий график (рис. 4.3,б). Парабола второй степени вполне удовлетворительно выравнивает эмпирический ряд, что подтверждается также расчетом критерия χ2 (табл. 4.9): при числе степеней свободы ν=5 значение χ2=0,6281 значительно меньше стандартных значений χ205=11,1 и χ201=15,1.
Средняя ошибка найденного уравнения регрессии составляет:
= 
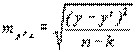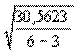= ±3,19. (4.44)
Она чуть меньше, чем в случае применения линейной модели, но парабола второй степени по-прежнему не допускает экстраполяции за пределы эмпирического ряда: при х=0 длина листа у=17,07 мм. Таким образом, с помощью этой функции невозможно добиться естественного, с биологической точки зрения, соотношения у=0 при х=0.
Повысить порядок параболы можно, взяв уравнение третьей степени: y=a+bx+cx2+dx3.
В этом случае придется решать систему, состоящую из четырех нормальных уравнений:
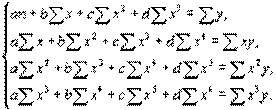(4.45)
Применительно к нашему примеру (табл. 4.10) это означает:
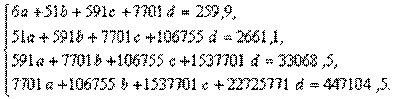
Решение этой системы дает значения неизвестных:d= 0,0122;c=-0,3804;b=6,1357;a=12,9739.
Искомое уравнение параболы третьей степени:у=12,9739+6,1357х-0,3804х2+0,0122х3.
Обратное вычисление (табл. 4.10) позволяет получить точки (y’) теоретической линии регрессии и построить по ним соответствующий график (рис.4.3,в). Вполне удовлетворительно выполненная интерполяция подтверждается также значением χ2=0,50, далеко не достигающим при ν=5 стандартных значений χ205=11,1 и χ201=15,1.
Средняя ошибка уравнения регрессии составляет:
= 
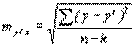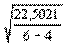= ±3,35 мм,
т.е. мало отличается от ошибок прямой линии и параболы второго порядка. Однако парабола третьей степени по-прежнему не допускает экстраполяции, ибо при нулевой ширине листа его длина равна 12,97 мм, что противоречит здравому смыслу.
Дальнейшее повышение степени параболы, сопровождаемое увеличением громоздкости расчетов, вряд ли способно существенно улучшить интерполяцию, а вопрос о соответствии параболической функции внутренней сущности изучаемой зависимости скорее всего таким путем решить не удастся.
Таблица 4.10.– Выравнивание эмпирической линии регрессии длины листа (у) на его ширину (х) у Melampyrum polonicum (Beauv.) Soo уравнением параболы третьей степени
| Расчеты для определения параметров уравнения | Построение теоретической линии регрессии | Расчет критерия χ2 | |||||||
| х5 | х6 | х3у | bх | cx2 | dx3 | a+bx+cx2+dx3=y’ | y-y’ | (y-y’)2 |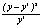 
|
| 1 1024 16807 100000 371293 1048576 | 1 4096 117649 1000000 4826809 16777216 | 19,5 1932,8 14337,4 51500,0 115122,8 264192,0 | 6,1357 24,5428 42,9499 61,357 79,7641 98,1712 | -0,3804 -6,0864 -18,6396 -38,04 -64,2876 -97,3824 | 0,0122 0,7808 4,1846 12,2 26,8034 49,9712 | 18,74 32,21 41,47 48,49 55,25 63,73 | 0,76 -2,01 0,33 3,01 -2,85 0,77 | 0,5776 4,0401 0,1089 9,0601 8,1225 0,5929 | 0,0308 0,1254 0,0026 0,1868 0,147 0,0093 |
| 1537701 | 2275771 | 447104,5 | – | – | – | 259,89 | 0,01 | 22,5021 | 0,5019 |
Примечание. Значения х,у,ху,х2,х2у,х3,х4 см. в табл. 4.5 – 4.8
В определенной мере здесь может помочь так называемый прием конечных разностей. Дело в том, что у параболы п-й степени конечная разность ее членов постоянна: Δпу =const, а следующая разность равна нулю: Δпу+1 =0. Пояснить сказанное можно примером параболы четвертой степени у=х4, где для удобства отброшены члены низшего порядка (х,х2 и х3), а также коэффициенты (табл. 4.11). Из таблицы видно, что разности (Δ) возрастающих порядков стремятся сблизиться и становятся одинаковыми на той разности, которая соответствует степени параболы.
Таблица 4.11.– Разложение параболы у=х4 на последовательные разности (Δ)
| х | х4 | Δ1 | Δ2 | Δ3 | Δ4 | Δ5 |
| 1 2 3 4 5 6 7 8 | 1 16 81 256 625 1296 2401 4096 | 15 65 175 369 671 1105 1695 | 50 110 194 302 434 590 | 60 84 108 132 156 | 24 24 24 24 | 0 0 0 |
Отсюда следует, что если хотим установить соответствие параболы внутренней сущности биологического явления, то эмпирическую линию регрессии надо «разложить» на последовательные разности (Δ1, Δ2,,…, Δп) и посмотреть, какие из них более или менее стабилизируются (полного совпадения, разумеется, ожидать нельзя). Если окажутся слабо «пульсирующие» разности, то можно воспользоваться параболой высшей степени.
В нашем примере с длиной и шириной листа у Melampyrum polonicumстабилизировать разности точек эмпирической линии регрессии (у/х) не удается (табл. 4.12) и, следовательно, параболическое интерполирование в этом случае описывает закономерность формально, не допуская экстраполяции.
При подборе интерполяционных формул следует обращаться к графическому анализу, сравнивая эмпирические линии регрессии с графиками встречающихся в биологии функций (рис. 4.4). В затруднительных случаях рекомендуется поиск выравнивающей функции посредством трансформации переменных. Этот прием заключается в построении нового графика, оси которого градуируются уже не натуральными значениями х и у, а такими значениями переменных, чтобы кривая на графике превратилась в прямую линию (рис. 4.4). Критерием соответствия данной формулы эмпирической линии регрессии служит рассеяние точек последней приблизительно вдоль прямой, которая на графике может располагаться как угодно. Если этого не происходит, надо переходить к испытанию другой формулы.
Формула 1 (рис. 4.4) обычно хорошо описывает зависимость между размерами органов растений и животных, а также распределение организмов внутри экологических стаций. Она носит название аллометрической функции.
Формулы 4 и 5 характеризуют взаимоотношение ареалов и количество видов в родах, но значение их этим не исчерпывается. Эти формулы (особенно формула 5) хорошо описывают известное в зоологии «правило оптимума», отражающее зависимость размеров тела животных от средней температуры данного пояса и, следовательно, от географической широты.
Таблица 4.12.– Разложение эмпирической линии регрессии длины листа (у)на его ширину (х) у Melampyrum polonicum (Beauv.) Sooна последовательные разности (Δ)
| у/х | Δ1 | Δ2 | Δ3 | Δ4 | Δ5 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 19,5 30,2 41,8 51,5 52,4 64,5 | 10,7 11,6 9,7 0,9 12,1 | 0,9 1,9 8,8 11,2 | 1,0 6,9 2,4 | 5,9 4,5 | 1,4 |
| Функции | Преобразования | ||
| х | у | ||
| y = axb | lgx | lgy |
| y = aebx | x | lgy |
| y = a+b/x | 1/x | y |
| 
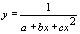
| x | (1/y)’ |
| 
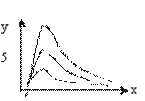
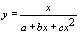
| x | (x/y)’ |
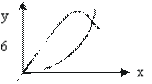
| y = ax + bx3 | x2 | y/x |
Рисунок 4.4 – Подбор интерполяционной формулы посредствомлинеаризации уравнения
Помимо изображенных на рис. 4.4 функций для описания биологических явлений могут применяться и другие формулы. Так, рост органов растений и животных во времени описывается S-образными кривыми, которые входят в обобщенный класс роста.
Циклические явления (временные изменения численности популяций, так называемые «волны жизни», а также временные ряды фенологических наблюдений, связывающие сроки наступления фенофаз с периодическими колебаниями климата и др.), могут быть описаны периодическими функциями типа:
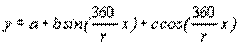, (4.46)
где r – число наблюдений за цикл через равные промежутки времени; х – порядковый номер наблюдения от х1=0 до хi=r-1.
В некоторых случаях оказываются полезными «гибридные» формулы, например, сочетание прямой линии с параболой y=a+bx+clgx или функция типа lg y=a+blg x+clg x2.
Применение перечисленных функций связано с использованием метода наименьших квадратов, для чего любая функция предварительно должна быть приведена к линейному виду. Следует отметить, что в настоящее время имеются специализированные пакеты описания зависимостей для ПЭВМ, а также статистические пакеты с широким набором функций для обработки исходных данных. Здесь на первый план для выбора функций выходит интуиция исследователя, а также опыт использования статистического описания данных в экологических исследованиях.
Множественная регрессия
Зависимость изменения одного признака от одновременного изменения двух или нескольких других признаков изучается методами множественной регрессии. С увеличением числа признаков и с переходом к нелинейной множественной регрессии сложность и громоздкость вычислений быстро нарастают, но в настоящее время это уже не является непреодолимым препятствием. Для лучшего понимания сути проблемы мы рассмотрим простейший, но чаще всего встречающийся в биометрической практике случай линейной множественной регрессии одного признака по двум другим.
Приведем математическое описание множественной регрессии. Параметры модели оцениваются по выборке объема п, полученной из популяции W. Предполагается, что x1i,….xpi, i=1,…,n – суть фиксированные значения независимых переменных Х1,,Хр, а уi – наблюдаемое значение переменной Y. Итак, выборка состоит из п наблюдений (y1; x11,…,xp1), (yn; x1n,…,xpn). Для модели множественной линейной регрессии имеем:
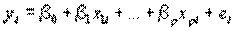, (4.47)
где β0, β1,…, βр – неизвестные параметры, а е1,…, еп – независимые случайные ошибки, распределенные по нормальному закону.
Например, 
есть модель множественной регрессии с x1 =sin z1 и x2= cos z1. В частности, если xi=xi, i=1,…, p, то получается модель полиномиальной регрессии 
. Наконец нужно помнить, что слово «линейная» подразумевает линейность относительно параметров, но не относительно независимых переменных. Так, например, 
не является линейной функцией параметров.
Как правило, любая программа в пакетах прикладных статистических программ для ПЭВМ при оценке параметров β0, β1,…, βр минимизирует сумму квадратов отклонений
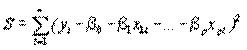. (4.48)
Эти оценки обычно называются (частными) коэффициентами регрессии и содержатся в выходных данных программ. Оценка уравнения множественной линейной регрессии может быть записана в виде
. (4.49)
В выходных данных программ обычно содержатся еще четыре величины. Первая, называемая остаточной суммой квадратов (или ошибок) SSR, есть значение S, которое получается при подстановке МНК-оценок вместо параметров, т.е.
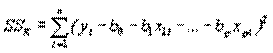. (4.50)
Если эту величину разделить на число степеней свободы νR=n-p-1, получаем несмещенную оценку дисперсии ошибок ϭ2, называемую остаточным средним квадратом ошибки MSR. Итак,
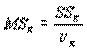. (4.51)
Указанные три величины обычно возникают в таблице дисперсионного анализа аналогично тому, как это показано в табл. 4.4. Четвертая величина – квадратный корень из MSR – называется стандартной ошибкой оценки. Описанные четыре величины приведены в табл. 4.13.
Полная сумма квадратов SST, деленная на число степеней свободы T, равна оценке дисперсии Y. ОтношениеSSD/SST=R2(иногда называемое коэффициентом детерминации) есть доля дисперсии Y, «объясненная» регрессией Y по X1,…,Xp. Итак, R2 является мерой качества подгонки, т.е. чем больше R2, тем лучше модель аппроксимирует Y.
Таблица 4.13.– Таблица дисперсионного анализа для моделимножественной линейной регрессии
| Источник дисперсии | Сумма квадратов | Степени свободы | Средний квадрат | F-отношение |
| Регрессия Отклонение от регрессии Полная |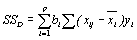  
| 
| 
| 
|
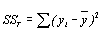
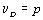
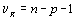
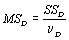
Пример. Изучалось октановое число бензина, содержащее различные концентрации добавок А и В.Пусть Y – октановое число, х1 – % первойдобавки, х2 – % второй добавки. Для описания зависимости Y от x1 и x2 использовалась множественная линейная регрессия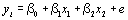 
. Каждая из двух независимых переменных принимала одно из четырех фиксированных значений, а значение Y их комбинациями (п=16):
| X1 | X2 | Y | X1 | X2 | Y |
| 2 | 2 3 4 5 | 96,3 95,7 99,9 99,4 | 4 | 2 3 4 5 | 96,2 100,1 103,2 104,3 |
| 3 | 2 3 4 5 | 95,1 97,8 99,3 104,9 | 5 | 2 3 4 5 | 97,8 102,2 104,7 108,8 |
С помощью программы множественной линейной регрессии ППП «Statistica» получены оценки b0=84,553; b1=1,833; b2=2,683, т.е. 
.
Результаты расчета обобщены в табл. 4.14.
Таблица 4.14.–Результаты расчетов множественной линейной регрессии
зависимости октанового числа бензина от концентрации добавок
| Источник дисперсии | Сумма квадратов | Степени свободы | Средний квадрат | F-отношение |
| Регрессия Отклонение от регрессии Полная | 211 25 236 | 2 13 15 | 105,5 1,94 | 54,5 |
Несмещенная оценка ϭ2 равна 1,94, а стандартная ошибка равна s=√1,94 =1,392 иR2=SSD/SST=211/236=0,893, следовательно, доля дисперсии, объясненнаяYпоX1 иX2,равна 89,3%. Так как значениеF-отношения равно 54,5, а стандартные значения, найденные по таблице Фишера с νR =13 и νD=2 степенями свободыF01=6,7 иF05=2,13, то нулевая гипотеза об отсутствии линейной регрессии междуYх1 и х2 не принимается. Таким образом, октановое число линейно зависит по меньшей мере от одной из добавокАилиВ.
Аллометрическая функция
Скорость роста разных органов растений и животных различна и изменяется в ходе онтогенеза. Важной особенностью одновременного роста двух или нескольких органов является то, что изменение скоростей их роста происходит синхронно, т.е. скоррелировано таким образом, что отношение скоростей роста остается приблизительно постоянной величиной. В этом и состоит биологическая сущность явления соотносительного (аллометрического) роста.
Связь между растущим органом и размером тела (или между двумя растущими органами) является нелинейной и обычно хорошо описывается аллометрической функцией y=bxα, где у – размер одного органа, х – размер другого органа; b – константа начального роста (при х=1 y=b); α – константа равновесия (аллометрический показатель), передающая относительную скорость (темп) роста одного органа по сравнению с другим.
Константа α имеет важный биологический смысл. При α=1 оба органа растут с одинаковой скоростью (случай изометрии) и их относительные размеры остаются постоянными. При α>1 (случай положительной аллометрии) из-за преимущества в скорости роста размер одного органа увеличивается относительно размера другого органа. При α<1 (отрицательнаяаллометрия) в связи с меньшей скоростью роста размер органа уменьшается относительно размера другого органа. Наконец, возможен случай энантиометрии (α<0), при котором абсолютные размеры органа в ходе онтогенеза уменьшаются (в зоологии уменьшение длины хвоста головастика по мере превращения его в лягушку). Ход аллометрической функции при первых трех пороговых значениях α-константы изображен на рис. 4.5.
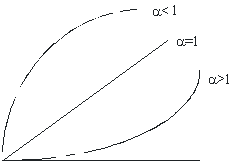
Рисунок 4.5 – Схематическое изображение аллометрической функции
при пороговых значениях константы
Методика аллометрии представляет собой еще один частный случай регрессионного анализа. Порядок работы остается обычным. Для использования метода наименьших квадратов аллометрическую функцию путем логарифмирования приводят к линейной форме: lgy=lgb+lgx. Тогда система нормальных уравнений приобретает вид
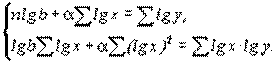(4.52)
Обратимся к конкретному примеру регрессии длины листа на ширину (использование уравнений прямой линии, парабол 2 и 3 степеней приводило к удовлетворительной интерполяции эмпирических данных, но не позволяло производить экстраполяцию). Применим к этому случаю аллометрическую функцию.
Таблица 4.16.– Выравнивание эмпирической линии регрессии длины листа (у)на его ширину (х) у Melampyrum polonicum уравнениемаллометрической функции (у')
| х | у | lgх | lgу | Lgx×lgy | Lg(x)2 | algx | Lgb+algx =lgy’ | Y’ |
| 1 4 7 10 13 16 | 19,5 30,2 41,8 51,5 52,4 64,5 | 0 0,6021 0,8451 1 1,1139 1,2041 | 1,29 1,48 1,6212 1,7118 1,7193 1,8096 | 0 0,8911 1,3701 1,7118 1,9151 2,1789 | 0 0,3625 0,7142 1 1,2408 1,4499 | 0 0,2557 0,3588 0,4246 0,473 0,5113 | 1,2681 1,5238 1,6269 1,6927 1,7411 1,7794 | 18,5 33,4 42,4 49,3 55,1 60,2 |
| – | – | 4,7652 | 9,6319 | 8,067 | 4,7674 | – | – | – |
Получаем систему нормальных уравнений:
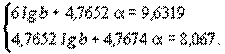
Решая которую, имеем: α=0,4246; lgb=1,2681 и b=18,54. Следовательно, искомая аллометрическая функция имеет вид у=18,54х0,4246 или в логарифмической форме lgy=1,2681+0,4246lgx. Используя последнюю запись, произведем обратное dsсчисление и находим точки теоретической линии регрессии (рис. 4.6). Как видно, аллометрическая функция хорошо описывает эмпирическую регрессию и позволяет экстраполировать опытные данные (при х=0 у=0).
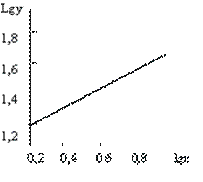
а б
Рисунок 4.6 –Аллометрическая функция, отражающая регрессию длины листа
на его ширину в натуральном (а) и логарифмическом масштабе (б)
1 – эмпирическая, 2 – теоретическая линии регрессии
График аллометрической функции, построенной в логарифмическом масштабе, имеет вид прямой линии с угловым коэффициентом a. На таком графике нагляднее видна относительная скорость роста: чем больше угол наклона прямой, тем эта скорость выше.
Из уравнения аллометрической функции lgy=lgb+algx видно, что a-константа есть не что иное, как коэффициент регрессии Rlgy/lgx. Таким образом, a-константа передает не только относительный темп роста двух органов (частей), но косвенно отражает и размерную зависимость изменения одного из них при изменении другого.
Поскольку мы имеем дело с двумя признаками (х и у), то существует возможность вычисления двух значений α иβ-констант, характеризующих темп роста признакауотносительно признаках(из уравнения lgy=lgb1+α1lgx) и признакахотносительно признакау(из уравнения lgх=lgb2+α2lgу), причем α1≠α2 и b1≠b2, но при полной корреляционной связи (r=±1) соблюдается соотношение α1=1:α2. С учетом сказанного в разделе 4.2 можно записать: α1=Rlgy/lgx=r (ϭlgy/ϭlgx) и α2= Rlgx/lgy=r (ϭlgx/ϭlgy),где r – коэффициент линейной корреляции, ϭ – соответствующие средние квадратичные отклонения.
Тогда соотношение между коэффициентом корреляции иα-константами может быть выражено уравнением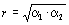 
.
Исследование аллометрических зависимостей может преследовать разные цели. Различен и биологический смысл получаемых при этомα-констант.
Дисперсионный анализ
Дата добавления: 2018-04-15; просмотров: 4561; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!