I. Непосредственное интегрирование
Задание 1.Вычислить неопределенный интеграл:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
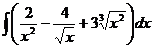
11. 
12. 
13. 
14. 
15. 
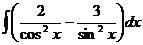
16. 
17. 
18. 
19. 
20. 
II. Метод замены переменной.
Задание 2. Проинтегрировать функции заменой переменной:
1) 
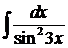
2) 
3) 
4) 
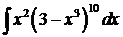
5) 
6) 
7. 
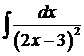
8. 
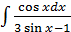
Определенный интеграл.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой 
.
Верхний предел интегрирования стандартно обозначается буквой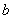 
.
Отрезок 
называется отрезком интегрирования.
Прежде чем мы перейдем к практическим примерам, поговорим об определенно интеграле.
Что такое определенный интеграл?Определенный интеграл – это ЧИСЛО.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл?С помощью формулы Ньютона-Лейбница:
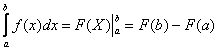
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию 
(неопределенный интеграл). Обратите внимание, что константа 
в определенном интеграле не добавляется. Обозначение 
является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись 
? Подготовка для применения формулы Ньютона-Лейбница.
|
|
|
2) Подставляем значение верхнего предела в первообразную функцию: 
.
3) Подставляем значение нижнего предела в первообразную функцию: 
.
4) Рассчитываем (без ошибок!) разность 
, то есть, находим число.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла 
не существует, поскольку отрезок интегрирования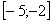 
не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: 
. Такого интеграла тоже не существует, так как в точках 
, 
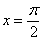отрезка 
не существует тангенса.
Для того чтобы определенный интеграл вообще существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.
Если для решения Вам предложен несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.
|
|
|
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.
Дата добавления: 2018-04-04; просмотров: 298; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!