Вказівки до виконання семестрового завдання (частина 2)
Завдання 1. Розглянемо типові задачі, які зустрічаються у різних варіантах.
Приклад 1.Скласти рівняння висоти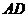 
трикутника, заданого точками 
, 
, 
.
Розв’язання.
Складемо загальне рівняння висоти 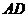за формулою: 
. Висота проходить через точку , значить, вважаємо 
, тобто 
.
Тому що 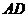є висотою трикутника, 
і 
перпендикулярні між собою. Вектор вважаємо за нормальний. 
.
Тепер можемо підставляти значення у формулу:
.
Далі маємо:
― рівняння прямої 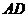у загальному вигляді.
Приклад 2.Трикутник заданий точками 
. Скласти рівняння прямої, що проходить через точку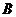 
паралельно 
.
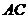Розв’язання.
Скористаємося канонічним рівнянням прямої: 
.
Шукана пряма проходить через точку 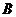, значить, 
. Вектор 
являється напрямним вектором для даної прямої, тобто
.
Запишемо рівняння прямої:
.
Звідки 
― шукане рівняння у загальному вигляді.
Приклад 3. Скласти рівняння прямої, що проходить через точку 
перпендикулярно прямій 
.
Розв’язання.
.
Умова перпендикулярності: 
. Звідки 
.
Рівняння шуканої прямої запишемо у вигляді 
:
.
або у загальному вигляді 
.
Приклад 4.Скласти рівняння медіани 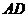трикутника, заданого точками , 
, 
.
Розв’язання.
Рівняння медіани будемо шукати як рівняння прямої, що проходить через дві точки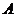 
та 
:
Координати точки знайдемо як координати середини відрізка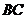 
:
.
Отже,
.
Точка має координати 
Можемо скласти рівняння медіани:
; 
.
Отримали рівняння медіани у канонічному вигляді. Приведемо це рівняння до загального вигляду:
; 
; 
або 
.
Маємо рівняння медіани 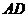у загальному вигляді .
Завдання 2. Обчислити об'єм тетраедра з вершинами в точках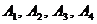 
і його висоту , опущену з вершини 
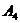на грань 
:
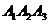Розв’язання.
З вершини 
проводимо вектори:
.
Об’єм піраміди обчислимо за формулою:
.
З іншого боку об’єм тетраедра обчислюється формулою:
Площа основи піраміди обчислюється через векторний добуток:
Завдання 3. Знайти відстань від точки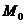 
до площини, що проходить через три точки 
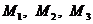, де
Розв’язання.
Відстань від точки 
до площини 
знаходять за формулою:
Рівняння площини, яка проходить через три точки 
, 
, 
:
Маємо,
Тепер знаходимо шукану відстань:
Завдання 4. Написати рівняння площини, що проходить через точку 
перпендикулярно вектору 
, де
Розв’язання.
Рівняння площини шукаємо у загальному вигляді:
.
За нормальний вектор можна взяти вектор :
.
.
Рівняння площини буде таким:
Завдання 5. Визначити кут між площинами
та 
.
Розв’язання.
Вектори, перпендикулярні до даних площин, будуть: 
, 
. Кут між площинами дорівнює куту між векторами 
і 
. Отже,
.
Завдання 6. Скласти канонічне рівняння прямої, заданої перетинанням площин
Розв’язання.
Рівняння прямої шукаємо у вигляді:
Знайдемо будь-яку точку 
, яка лежить на прямій, по якій перетинаються площини. Положимо 
, тоді маємо:
Розв’язуючи цю систему, отримуємо: 
.
Отже, 
― точка, що належить прямій.
Знайдемо координати напрямного вектора 
за формулою:
Тоді
, 
.
Тобто канонічне рівняння шуканої прямої записати можна так:
,
Завдання 7. Знайти точку перетину прямої 
з площиною 
.
Розв’язання.
Запишемо канонічне рівняння прямої у параметричному вигляді:
Отримані вирази для 
підставимо у рівняння площини:
.
Звідки 
.
Підставивши значення у параметричне рівняння прямої, знайдемо загальну точку прямої і площини:
Отже, 
– шукана точка перетину прямої і площини.
Дата добавления: 2018-04-05; просмотров: 395; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!