ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2. Исследование параметров неординарных потоков требований
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. Потоком требований (событий) называется последовательность однородных требований, появляющихся одно за другим в случайные моменты времени. Примеры: поток вызовов на телефонной станции; прибытие поездов на станцию; поток сбоев ЭВМ; поток заявок на проведение регламентных работ в вычислительном центре и т.п.
Потоки требований имеют такие свойства, как стационарность, ординарность и отсутствие последействия.
Свойство стационарности означает, что с течением времени вероятностные характеристики потока не меняются. Поток можно назвать стационарным, если для любого числа k требований, поступивших за промежуток времени длиной дt, вероятность поступления требований зависит только от величины промежутка и не зависит от его расположения на оси времени.
Свойство ординарности означает практическую невозможность группового поступления требований. Поэтому поток требований можно назвать ординарным тогда, когда вероятность поступления двух или более требований за любой бесконечно малый промежуток времени Δt есть величина бесконечно малая более высокого порядка, чем △t.
Свойство отсутствия последействия означает независимость вероятностных характеристик потока от предыдущих событий. Иными словами, вероятность поступления k требований в промежуток [t1,t2] зависит от числа, времени поступления и длительности обслуживания требований до момента t1.
|
|
|
К основным характеристикам случайного потока относят ведущую функцию и интенсивность.
Ведущая функция случайного потока есть математическое ожидание числа требований в промежутке [0, t). Функция - неотрицательная, неубывающая и в практических задачах теории распределения информации непрерывна и принимает только конечные значения.
Интенсивностью λ потока событий называется среднее число (математическое ожидание числа) событий, приходящееся на единицу времени. Для стационарного потока λ = const; для нестационарного потока интенсивность в общем случае зависит от времени: λ= λ(t).
Потоки требований различают по многим видам, но мы рассмотрим наиболее встречающиеся, а именно простейшие потоки и их модификации, потоки Пальма и потоки Эрланга.
Простейшие потоки. Если поток требований обладает свойствами стационарности, ординарности и отсутствия последствия, то такой поток называется простейшим (или пуассоновским) потоком требований.
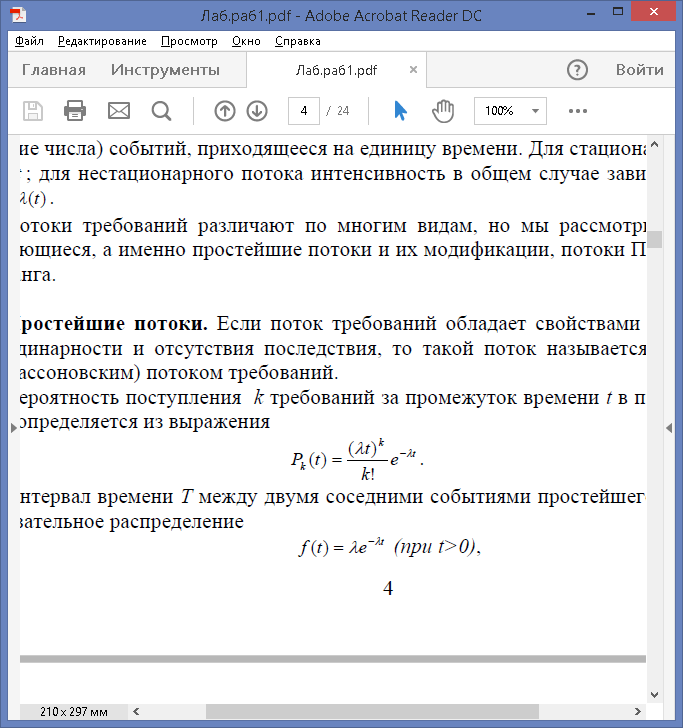
Вероятность поступления k требований за промежуток времени t в пуассоновском потоке определяется из выражения
|
|
|
Интервал времени Т между двумя соседними событиями простейшего потока имеет показательное распределение
где λ = 1/ М [Т ] - величина, обратная среднему значению интервала Т.
Математическое ожидание, дисперсия и среднеквадратическое отклонение промежутка T:
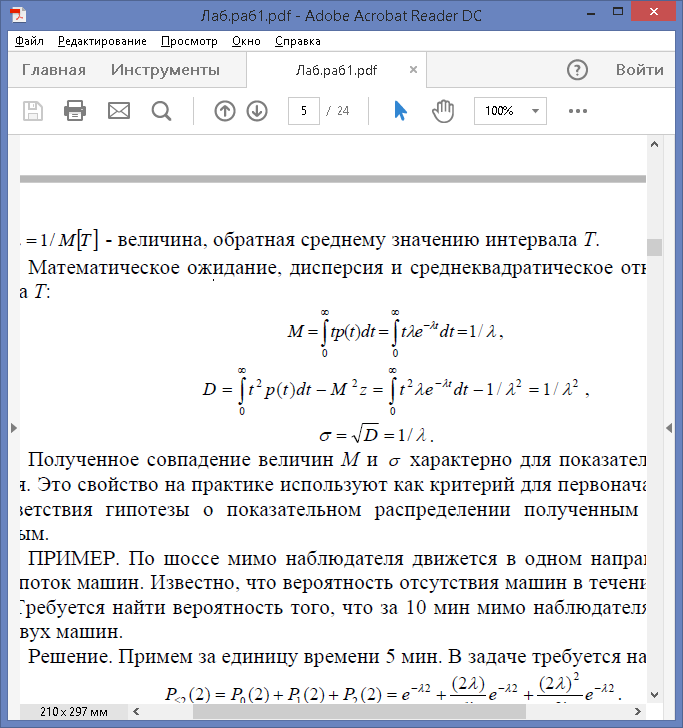
Полученное совпадение величин M и σ характерно для показательного распределения. Это свойство на практике используют как критерий для первоначальной проверки соответствия гипотезы о показательном распределении полученным статистическим данным.
ПРИМЕР. По шоссе мимо наблюдателя движется в одном направлении простейший поток машин. Известно, что вероятность отсутствия машин в течение 5 минут равна 0,5. Требуется найти вероятность того, что за 10 мин мимо наблюдателя пройдет не более двух машин.
Решение. Примем за единицу времени 5 мин. В задаче требуется найти
Из условия следует P0(1) = 0,5, т.е. e -λ = 0,5, следовательно, λ = ln2. Таким образом, в предыдущее уравнение подставляем λ и получим Ps2 (2) = 0,84.
Простейший поток с возможной нестационарностью. Простейшим потоком с возможной нестационарностью (нестационарным простейшим потоком) является поток, обладающий свойствами ординарности, отсутствием последействия и имеющий в каждый момент времени t конечное мгновенное значение параметра λ(t).
|
|
|
Мгновенная интенсивность нестационарного простейшего потока λ(t) определяется как предел отношения среднего числа событий, которые произошли за элементарный интервал времени (t, t + △t), к длине △t этого интервала, когда △t → 0 . Среднее число событий, наступающих в интервале времени т, следующем непосредственно за моментом
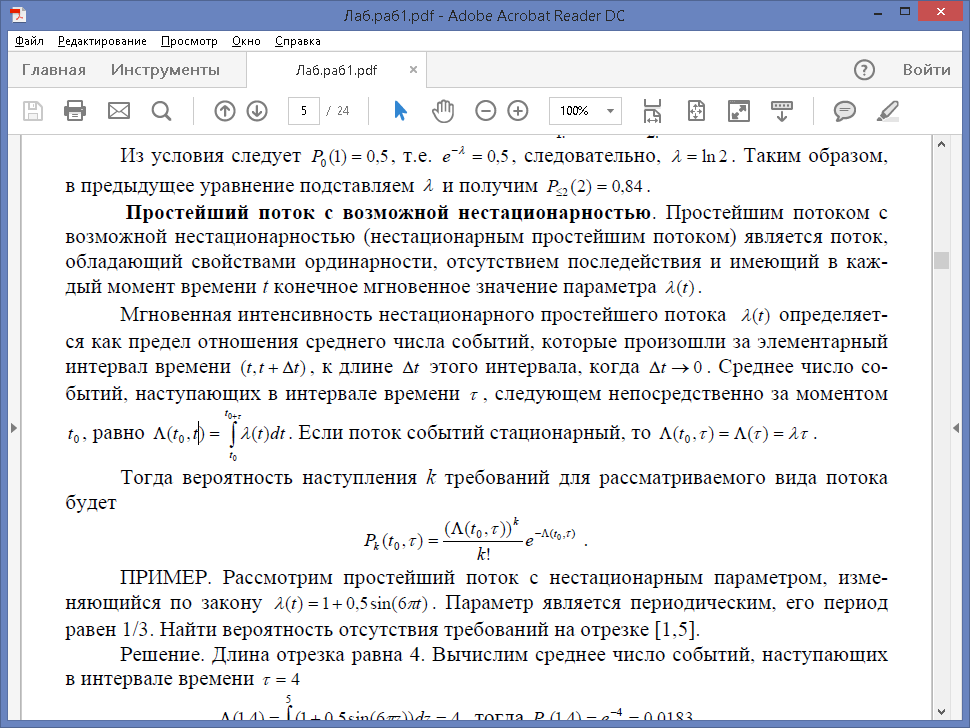
t0, равно Если поток событий стационарный, то
Тогда вероятность наступления k требований для рассматриваемого вида потока будет
ПРИМЕР. Рассмотрим простейший поток с нестационарным параметром, изменяющийся по закону λ(t) = 1 + 0,5sin(6πt). Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1,5].
Решение. Длина отрезка равна 4. Вычислим среднее число событий, наступающих в интервале времени τ = 4
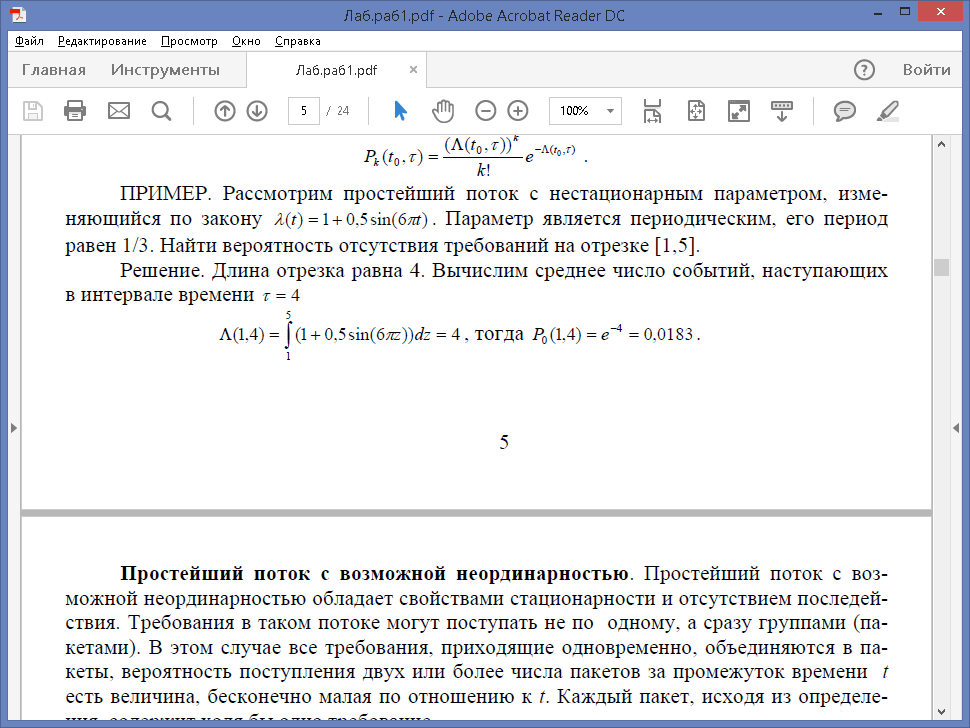
Простейший поток с возможной неординарностью. Простейший поток с возможной неординарностью обладает свойствами стационарности и отсутствием последействия. Требования в таком потоке могут поступать не по одному, а сразу группами (пакетами). В этом случае все требования, приходящие одновременно, объединяются в пакеты, вероятность поступления двух или более числа пакетов за промежуток времени t есть величина, бесконечно малая по отношению к t. Каждый пакет, исходя из определения, содержит ходя бы одно требование.
|
|
|
Вероятность поступления k требований для потока с возможной неординарностью с учетом вероятности pm нахождения m требований в пакете
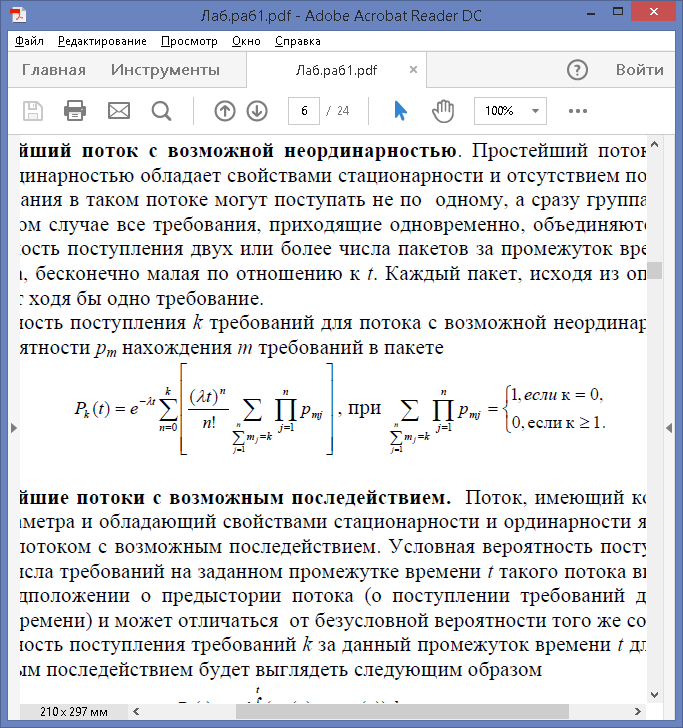
Простейшие потоки с возможным последействием. Поток, имеющий конечное значение
параметра и обладающий свойствами стационарности и ординарности является простейшим потоком с возможным последействием. Условная вероятность поступления некоторого числа требований на заданном промежутке времени t такого потока вычисляется при предположении о предыстории потока (о поступлении требований до этого промежутка времени) и может отличаться от безусловной вероятности того же события.
Вероятность поступления требований k за данный промежуток времени t для потока с возможным последействием будет выглядеть следующим образом
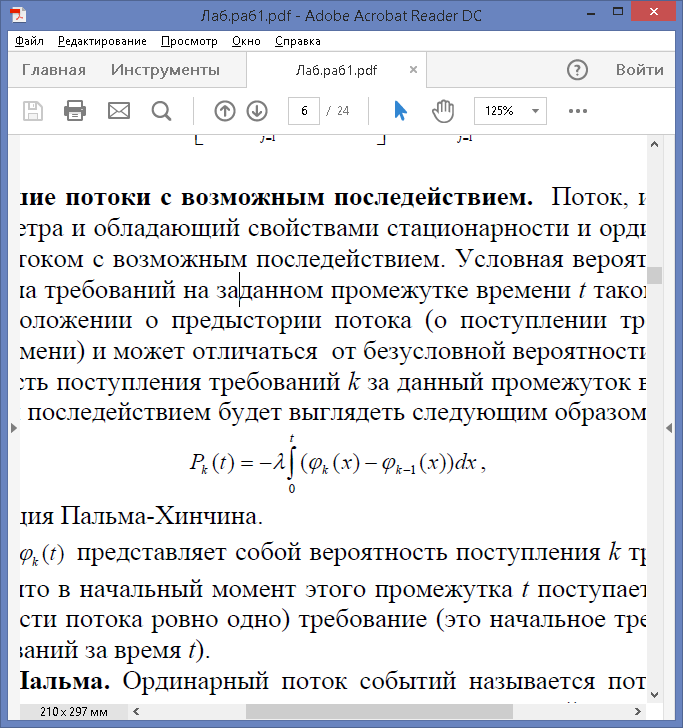
где φк (t) - функция Пальма-Хинчина.
Функция φk (t) представляет собой вероятность поступления k требований за время t при условии, что в начальный момент этого промежутка t поступает хотя бы одно (а в силу ординарности потока ровно одно) требование (это начальное требование не входит в число к требований за время t).
Потоки Пальма. Ординарный поток событий называется потоком Пальма (или рекуррентным потоком, или потоком с ограниченным последействием), если интервалы времени T1,T2,... между последовательными событиями представляют собой независимые, одинаково распределенные случайные величины.
В связи с одинаковостью распределений T1,T2,... поток Пальма всегда стационарен. Простейший поток является частным случаем потока Пальма; в нем интервалы между событиями распределены по показательному закону.
Потоки Эрланга. Потоком Эрланга n-го порядка называется поток событий, получающийся «прореживанием» простейшего потока, когда сохраняется каждая n-я точка (событие) в потоке, а все промежуточные выбрасываются.
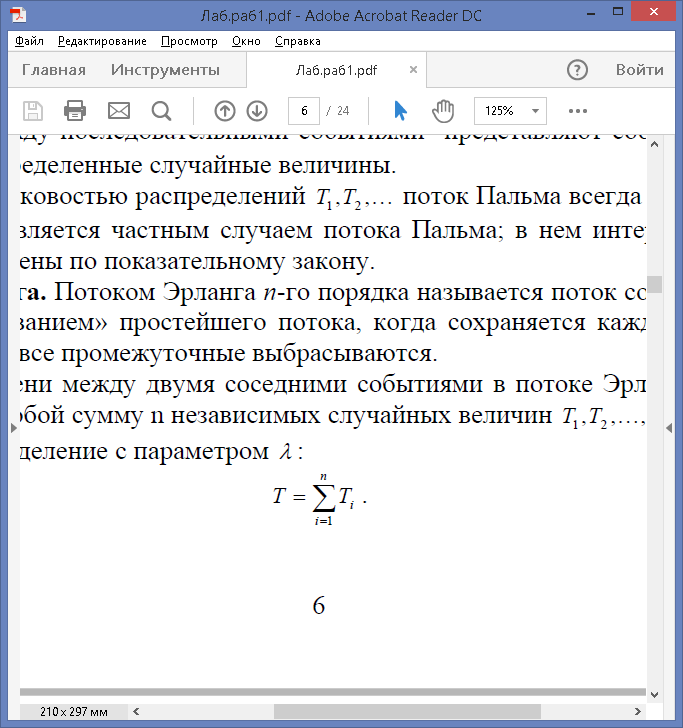Интервал времени между двумя соседними событиями в потоке Эрланга n-го порядка представляет собой сумму n независимых случайных величин T1, T2,..., Тк, имеющих показательное распределение с параметром λ:
Закон распределения случайной величины Т называется законом Эрланга n-го порядка и имеет плотность
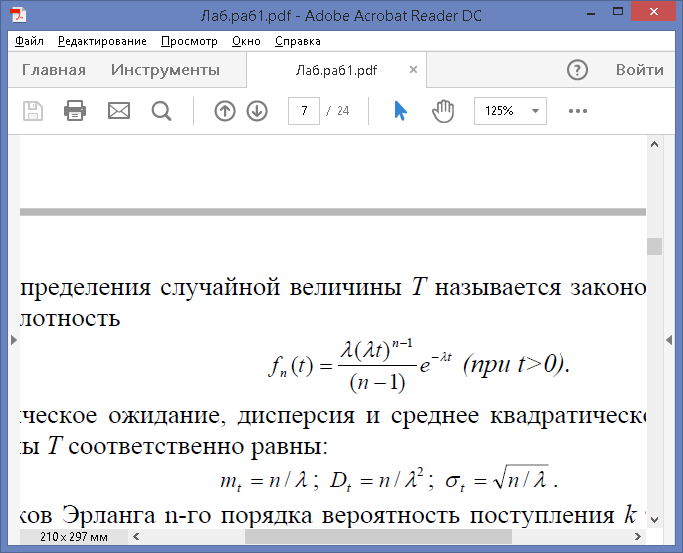
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины Т соответственно равны:
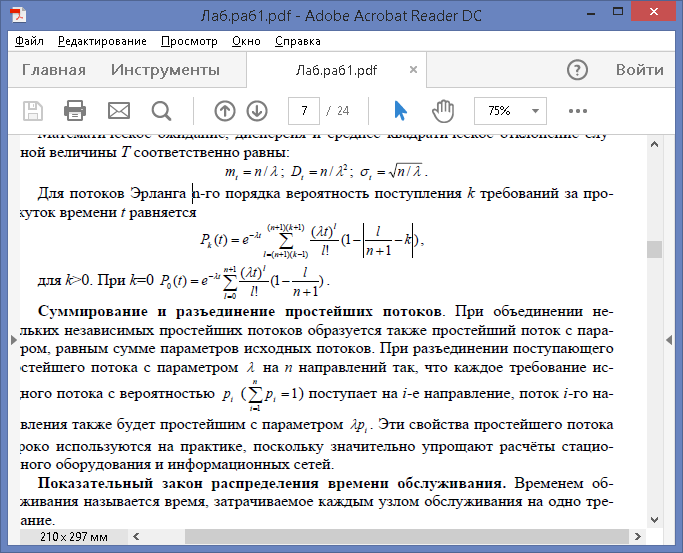
Для потоков Эрланга n-го порядка вероятность поступления k требований за промежуток времени t равняется
Суммирование и разъединение простейших потоков. При объединении нескольких независимых простейших потоков образуется также простейший поток с параметром, равным сумме параметров исходных потоков. При разъединении поступающего простейшего потока с параметром λ на п направлений так, что каждое
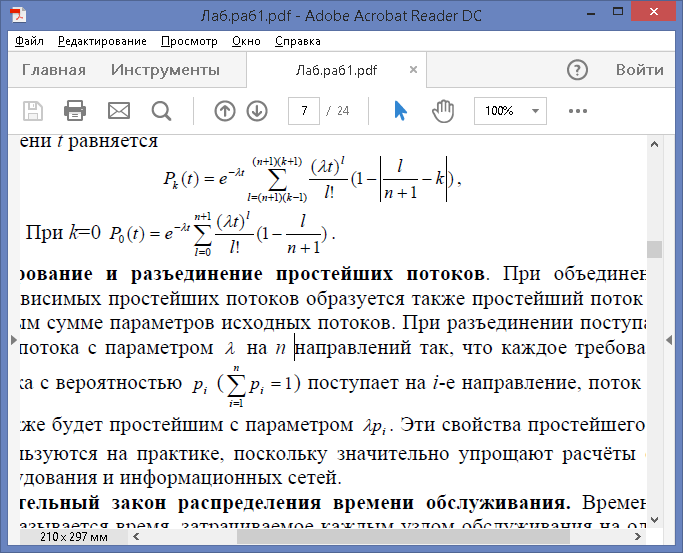требование исходного потока с вероятностью поступает на i-е
направление, поток i-го направления также будет простейшим с параметром λpi. Эти свойства простейшего потока широко используются на практике, поскольку значительно упрощают расчеты стационарного оборудования и информационных сетей.
Показательный закон распределения времени обслуживания. Временем обслуживания называется время, затрачиваемое каждым узлом обслуживания на одно требование.
Время обслуживания характеризует пропускную способность каждого узла обслуживания, не связано с оценкой качества обслуживания и является случайной величиной.
Это объясняется неидентичностью узлов обслуживания и различием в спросе на обслуживание отдельных требований. Например, поступающие на ремонт вагоны имеют не исправности самого различного характера, попадают в различные ремонтные бригады, поэтому время на обслуживание для различных вагонов не будет одинаковым.
Во многих задачах теории массового обслуживания закон распределения времени обслуживания предполагается показательным и описывается выражением
Параметр µ характеризует среднюю скорость обслуживания требований.
ВАРИАНТЫ ЗАДАНИЙ
| № варианта | ||||
| № задачи | № задачи | Число каналов | Число каналов | |
| 1 | 2,6,9 | 3,7,10 | 5 | 7 |
| 2 | 1,4,8 | 5,11,16 | 2 | 6 |
| 3 | 3,12,15 | 10,13,14 | 3 | 5 |
| 4 | 5,20,22 | 17,19,21 | 4 | 4 |
| 5 | 4,9,14 | 30,26,24 | 5 | 3 |
| 6 | 6,29,25 | 9,19,28 | 6 | 2 |
| 7 | 7,17,27 | 29,22,9 | 4 | 1 |
| 8 | 8,13,18 | 1,6,11 | 3 | 4 |
| 9 | 9,14,19 | 16,21,26 | 2 | 3 |
| 10 | 11,16,21 | 27,22,17 | 7 | 5 |
| 11 | 10,15,20 | 3,8,13 | 5 | 6 |
| 12 | 12,17,22 | 30,25,20 | 4 | 7 |
| 13 | 27,22,17 | 8,13,18 | 2 | 4 |
| 14 | 29,30,24 | 26,21,17 | 5 | 3 |
| 15 | 13,18,23 | 23,28,3 | 2 | 5 |
| 16 | 26,20,15 | 4,9,14 | 4 | 2 |
| 17 | 28,23,18 | 11,16,21 | 5 | 4 |
| 18 | 29,24,19 | 7,12,17 | 6 | 1 |
| 19 | 14,19,24 | 15,20,25 | 3 | 7 |
| 20 | 24,17,12 | 18,23,28 | 1 | 4 |
| 21 | 12 | 5 | 2 | 2 |
| 22 | 15 | 14 | 3 | 4 |
| 23 | 18 | 28 | 4 | 5 |
| 24 | 25 | 12 | 6 | 2 |
| 25 | 16 | 22 | 7 | 1 |
| 26 | 30 | 34 | 3 | 5 |
| 27 | 8 | 13 | 1 | 7 |
| 28 | 23 | 39 | 2 | 3 |
| 29 | 17 | 23 | 3 | 5 |
| 30 | 24 | 19 | 4 | 6 |
| 31 | 17 | 38 | 5 | 7 |
| 32 | 25 | 35 | 4 | 2 |
| 33 | 5 | 24 | 2 | 4 |
| 34 | 21 | 37 | 1 | 5 |
| 35 | 9 | 21 | 6 | 6 |
| 36 | 22 | 36 | 4 | 4 |
| 37 | 18 | 25 | 3 | 1 |
| 38 | 20 | 32 | 6 | 3 |
ЗАДАНИЕ
1. Дан пуассоновский поток с параметром 2 мин-1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 1 до 2 минут.
2. Производится наложение («суперпозиция») двух простейших потоков с интенсивностями λ1 и λ2. Будет ли поток, получившийся в результате наложения, простейшим, и если да, то с какой интенсивностью?
3. Производится случайное прореживание простейшего потока событий с интенсивностью λ; каждое событие, независимо от других, с вероятностью p сохраняется в потоке, а с вероятностью l-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
4. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 2 машины в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, в течение которого ему придется ждать машину; определить математическое ожидание и среднее квадратичное отклонение.
5. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 4 машины в минуту. Шоссе имеет развилку в два направления. Вероятность движения машин в первом направлении равна 0,12, а во втором - 0,88. Определить интенсивности движения автомобилей в обоих направлениях.
6. 
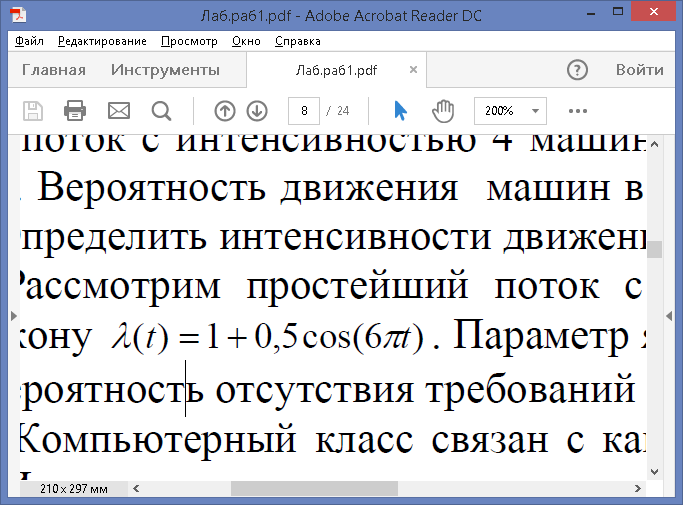Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону . Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;9].
7. Компьютерный класс связан с каналом Интернет через 10-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 540 бит/с, 120 бит/с, 40 бит/с, 170 бит/с, 350 бит/с, 60 бит/с, 742 бит/с, 153 бит/с, 500 бит/с, 100 бит/с. Поток данных подчиняется пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.
8. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону M(t) = 1 + 0,5 sin(6^t) . Параметр является периодическим, его период равен 1/4. Найти вероятность поступления одного, двух и трех требований.
9. Для простейшего потока с нестационарным параметром, определяемым равенством λ(t) = 3 + 2-t, найти вероятность поступления двух требований на промежутке времени [3;8].
10. По железной дороге мимо наблюдателя движется в одном направлении простейший поток поездов. Известно, что вероятность отсутствия поездов в течение 10 минут равна 0,8. Требуется найти вероятность того, что за 20 мин мимо наблюдателя пройдет не более трех поездов.
11. Производится случайное прореживание простейшего потока событий с интенсивностью λ = 4; каждое событие, независимо от других, с вероятностью p=0,6 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
12. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону λ(t) = 2 + 0,5 sin(4πt). Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [1;5].
13. Дан пуассоновский поток с параметром 1 мин -1. Найти вероятность того, что длина интервала между соседними требованиями составляет от 2 до 4 минут.
14. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 8 машин в минуту. Шоссе имеет развилку в три направления. Вероятность движения машин в первом направлении равна 0,12, во втором - 0,68, в третьем - 20. Определить интенсивности движения автомобилей во всех направлениях.
15. Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 6 машин в минуту. Человек выходит на шоссе, чтобы остановить первую попавшуюся машину, идущую в данном направлении. Найти закон распределения времени Т, которое ему придется ждать; определить его математическое ожидание и среднее квадратичное отклонение.
16. Для простейшего потока с нестационарным параметром, определяемым равенством λ(t) = 7 – 5-t, найти вероятность поступления двух требований на промежутке времени [1;10].
17. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью λ = 0,307. Найти вероятность того, что за час не поступит ни одного требования (вагона) на ремонт.
18. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону F(t) = 1 – e-1,5t, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 15 мин.
19. Для простейшего потока с нестационарным параметром, определяемым равенством λ(t) = 3 + 2-2t, найти вероятность поступления двух требований на промежутке времени [2;6].
20. В пункт текущего отделочного ремонта вагонов поступает требование на ремонт. Поток требований можно считать простейшим с интенсивностью А = 0,517. Найти вероятность того, что за час поступит одного требование (вагон) на ремонт.
21. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону F(t) = 1 - e~0,5t, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 5 мин.
22. Производится случайное прореживание простейшего потока событий с интенсивностью λ = 0,7; каждое событие, независимо от других, с вероятностью p=0,75 сохраняется в потоке, а с вероятностью 1-р выбрасывается. Каким будет поток, получающийся в результате прореживания простейшего потока?
23. Производится разбиение случайного простейшего потока событий с интенсивностью А = 4,9 на три потока. Вероятности попадания событий в тот или иной поток соответственно равны p1=0,2, p2=0,54, p3=0,26. Определить интенсивности каждого получившегося потока в результате разбиения.
24. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону F(t) = 4 – e-1,6t, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 8 мин.
25. В пункт текущего отделочного ремонта вагонов поступают требования на ремонт. Поток требований можно считать простейшим с интенсивностью А = 0,617 . Найти вероятность того, что за час поступит одно требование (вагон) на ремонт.
26. Производится разбиение случайного простейшего потока событий с интенсивностью λ = 1,6 на 2 потока. Вероятности попадания событий в тот или иной поток соответственно равны p1=0,44, p2=0,56. Определить интенсивности каждого получившегося в результате разбиения потока.
27. Компьютерный класс связан с каналом Интернет через 5-канальный концентратор. Интенсивности передачи данных по каждому из 10 каналов равны соответственно 541 бит/с, 110 бит/с, 44 бит/с, 171 бит/с, 356 бит/с. Поток данных подчинятся пуассоновскому закону распределения. Определить интенсивность передачи данных в канале Интернет.
28. Рассмотрим простейший поток с нестационарным параметром, изменяющимся по закону λ(t) = 2 + 0,5sin(4πt). Параметр является периодическим, его период равен 1/3. Найти вероятность отсутствия требований на отрезке [4;9].
29. На вокзал прибывает пуассоновский поток поездов, в среднем 2 поезда за 5 минут. Найти вероятность того, что за 15 минут прибудут 3 поезда.
30. Время обслуживания для аппаратов некоторой системы массового обслуживания распределено по показательному закону F(t) = 1 – e-4,5t, где t - время в минутах. Найти вероятность того, что обслуживание продлится не более 20 мин.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Методические указания
Классификация систем массового обслуживания. Большинство задач на железнодорожном транспорте связано с системами массового обслуживания.
Системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо видов услуг, а, с другой стороны, происходит удовлетворение этих запросов, называются системами массового обслуживания.
Система массового обслуживания включает следующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (обслуживающий аппарат, канал обслуживания), выходящий поток требований.
Системы массового обслуживания классифицируют по разным признакам. Одним из признаков является ожидание требования начала обслуживания. В соответствии с этим признаком системы подразделяются на следующие виды:
1) системы массового обслуживания с потерями (отказами);
2) системы массового обслуживания с ожиданием;
3) системы массового обслуживания с ограниченной длиной очереди;
4) системы массового обслуживания с ограниченным временем ожидания.
Системы массового обслуживания, у которых требования, поступающие в момент,
когда все приборы обслуживания заняты, получают отказ и теряются, называются системами с потерями или отказами.
Системы массового обслуживания, у которых возможно появление как угодно длинной очереди требований к обслуживающему устройству, называются системами с ожиданием.
Системы массового обслуживания, допускающие очередь, но с ограниченным числом мест в ней, называются системами с ограниченной длиной очереди.
Системы массового обслуживания, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.
По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.
По месту нахождения источника требований СМО делятся на разомкнутые, когда источник находится вне системы, и замкнутые, когда источник находится в самой системе. К последнему виду относится, например, станочный участок, в котором станки являются источником неисправностей, а следовательно, и требований на их обслуживание.
Одной из форм классификации систем массового обслуживания является кодовая (символьная) классификация Д. Кендалла. При этой классификации характеристику системы записывают в виде трех, четырех или пяти символов, например А | B | S, где А — тип распределения входящего потока требований, В — тип распределения времени обслуживания, S — число каналов обслуживания.
Для экспоненциального распределения принимают символ М, для любого (произвольного) распределения - символ G. Запись М | М | 3 означает, что входящий поток требований пуассоновский (простейший), время обслуживания распределено по экспоненциальному закону, в системе имеется три канала обслуживания.
Четвертый символ указывает допустимую длину очереди, а пятый — порядок отбора (приоритета) требований.
Уравнение Колмогорова для вероятностей состояний. Системы, представляемые в виде непрерывной цепи Маркова, обычно исследуют с помощью уравнения Колмогорова для вероятностей состояний.
Плотностью вероятности перехода λij из состояния Si в состоянии Sj называется
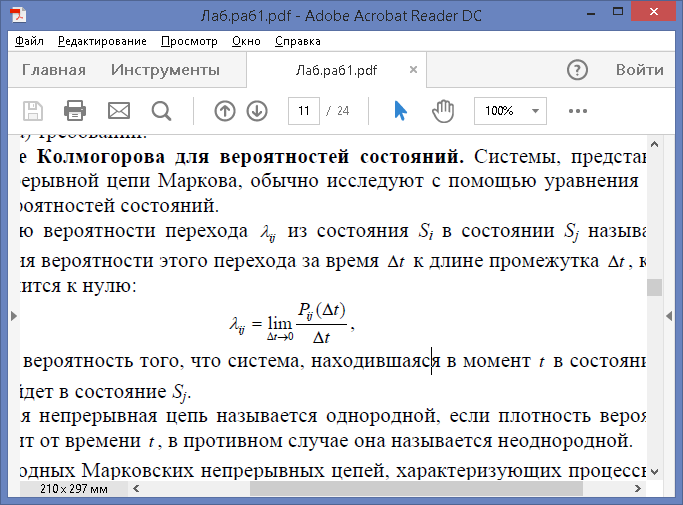предел отношения вероятности этого перехода за время △t к длине промежутка △t, когда последний стремится к нулю:
где Pij (△t) - вероятность того, что система, находившаяся в момент t в состоянии Si, за время △t перейдет в состояние Sj.
Марковская непрерывная цепь называется однородной, если плотность вероятностей λij не зависит от времени t, в противном случае она называется неоднородной.
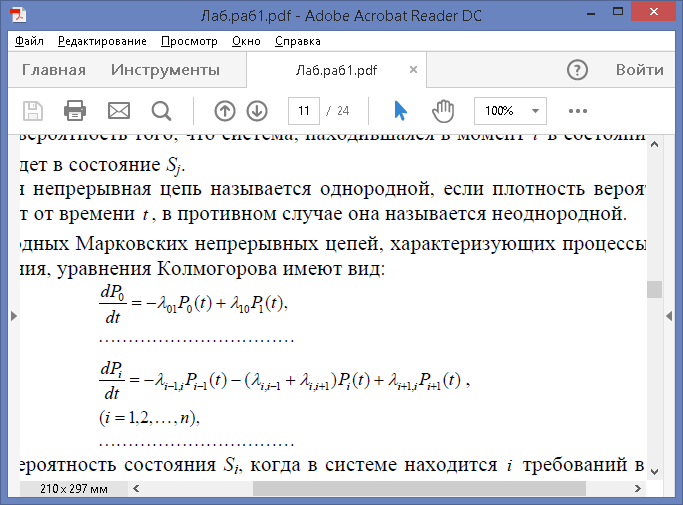Для однородных Марковских непрерывных цепей, характеризующих процессы гибели и размножения, уравнения Колмогорова имеют вид:
где Pi (t ) - вероятность состояния Si, когда в системе находится i требований в момент времени t; n +1- общее число возможных состояний So,Si,...,Sn.
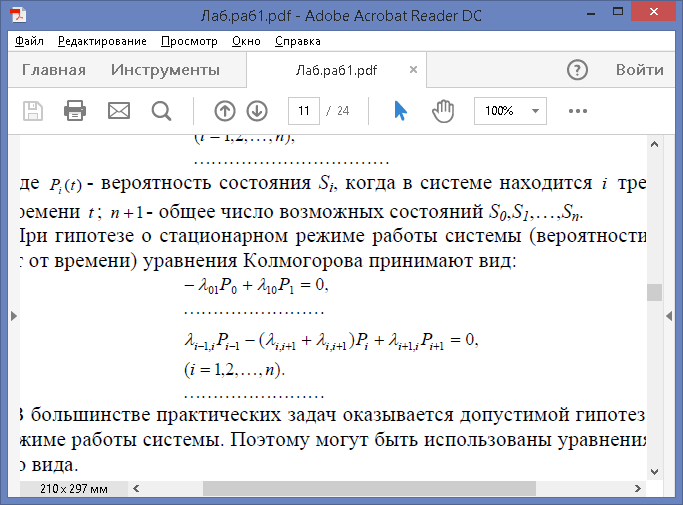
При гипотезе о стационарном режиме работы системы (вероятности состояний не зависят от времени) уравнения Колмогорова принимают вид:
-
В большинстве практических задач оказывается допустимой гипотеза о стационарном режиме работы системы. Поэтому могут быть использованы уравнения Колмогорова второго вида.
Математические модели систем массового обслуживания, приводимые ниже, соответствуют уравнениям Колмогорова для стационарного режима работы системы при условиях простейшего потока входящих требований и экспоненциального закона распределения времени обслуживания.
Системы массового обслуживания с отказами. СМО с отказами является такая система, в которой приходящие для обслуживания требования, в случае занятости всех каналов обслуживания, сразу ее покидают.
Вероятности состояний системы определяются из выражения
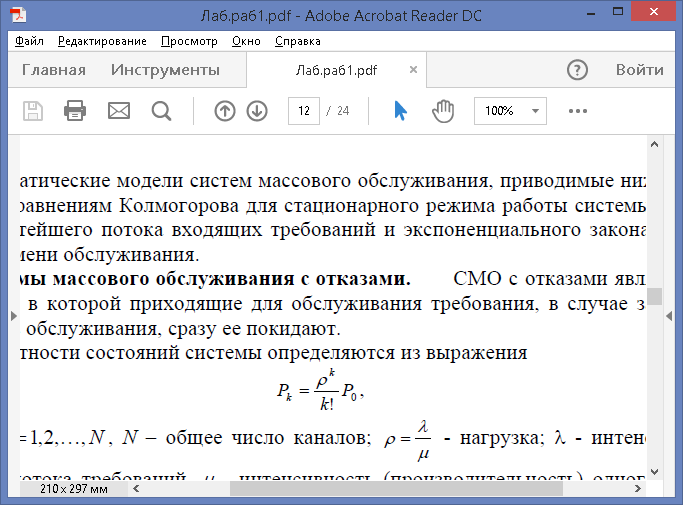
где k =1,2…,N , N – общее число каналов;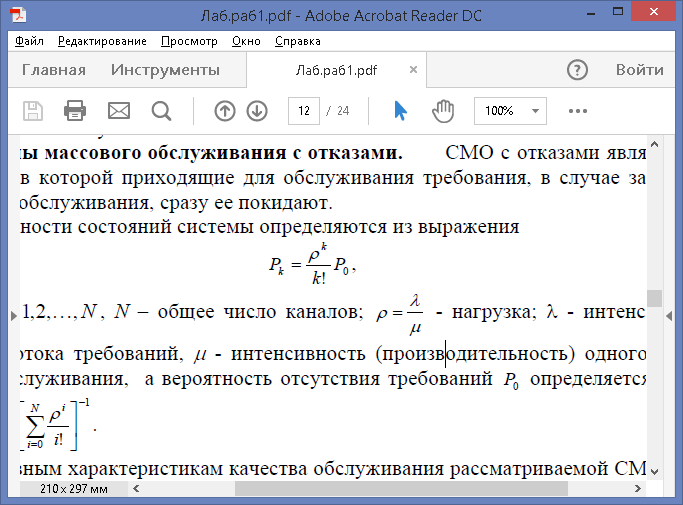 
– нагрузка; λ - интенсивность входящего потока требований, μ - интенсивность (производительность) одного канала (прибора) обслуживания, а вероятность отсутствия требований Р0
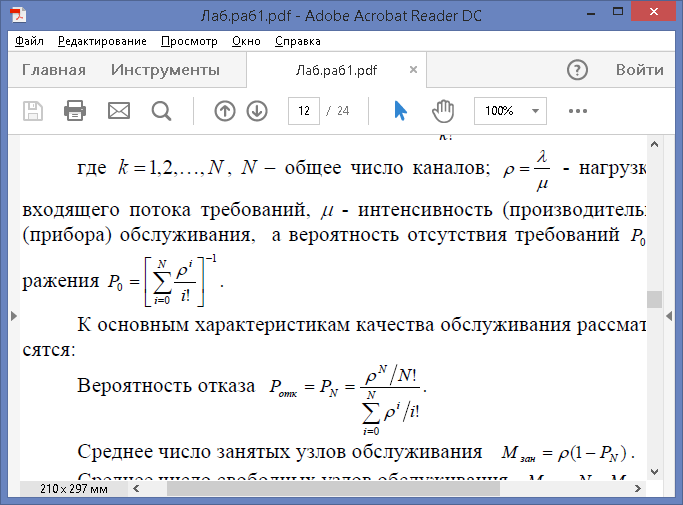
определяется из выражения
К основным характеристикам качества обслуживания рассматриваемой СМО относятся:
Вероятность отказа
Среднее число занятых узлов обслуживания Мзан = р(1 - PN).
Среднее число свободных узлов обслуживания Мсв = N - Мзан.
В системах с отказами события отказа и обслуживания составляют полную группу событий, отсюда
Относительная пропускная способность определяется по формуле
Абсолютная пропускная способность СМО с отказами равняется
Коэффициент занятости узлов обслуживания определяется отношением средним числом занятых каналов к общему числу каналов
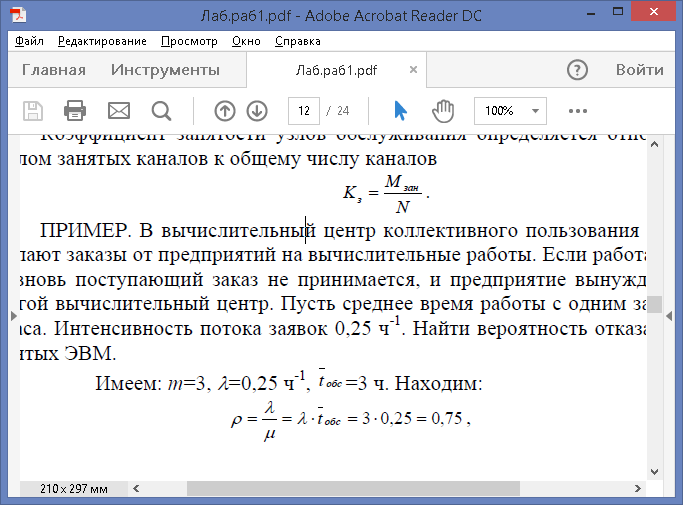
ПРИМЕР. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Пусть среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 ч-1. Найти вероятность отказа и среднее число занятых ЭВМ.
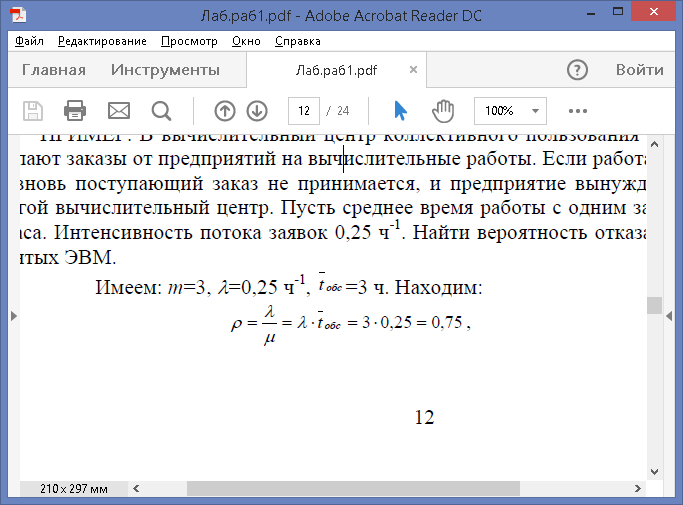
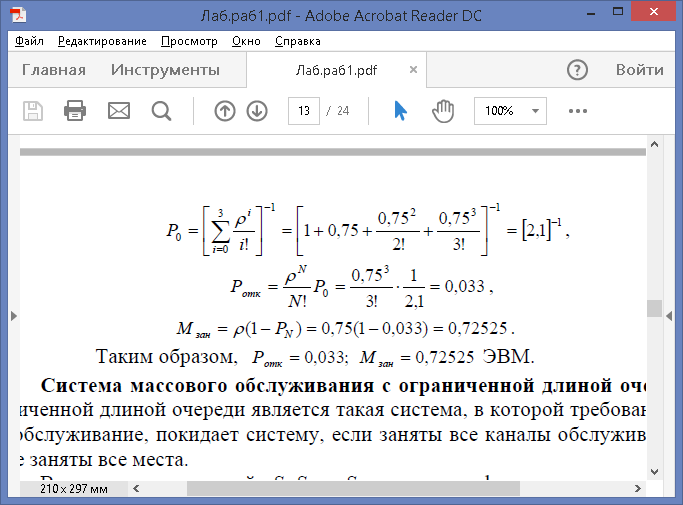
Таким образом, Ротк = 0,033; Мзан = 0,72525 ЭВМ.
Система массового обслуживания с ограниченной длиной очереди. СМО с ограниченной длиной очереди является такая система, в которой требование, поступающее на обслуживание, покидает систему, если заняты все каналы обслуживания, и в накопителе заняты все места.
Вероятности состояний S0,S1,...,SN находят по формуле
Вероятности состояний SN+1,SN+2,…,SN+l определяют с помощью формулы
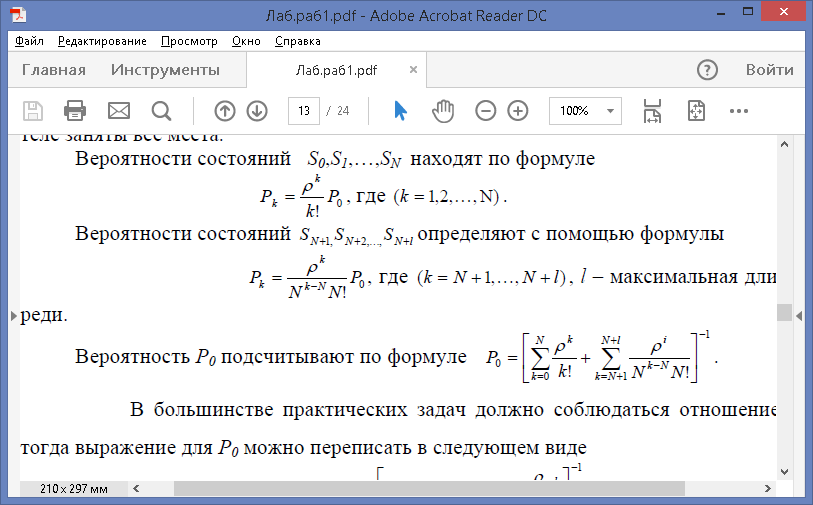
l – максимальная длина очереди
Вероятность P0 подсчитывают по формуле
Среднее число каналов, занятых в обслуживании, и коэффициент занятости определяются:
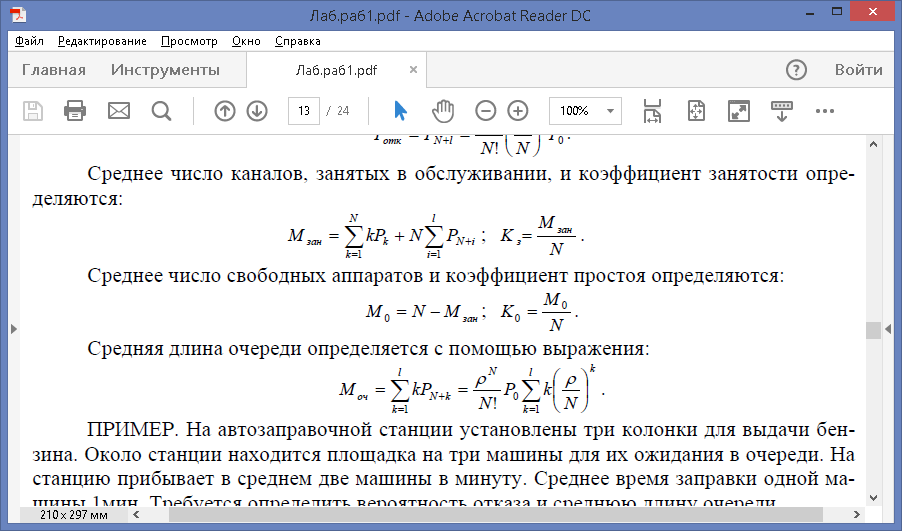
Среднее число свободных аппаратов и коэффициент простоя определяются:
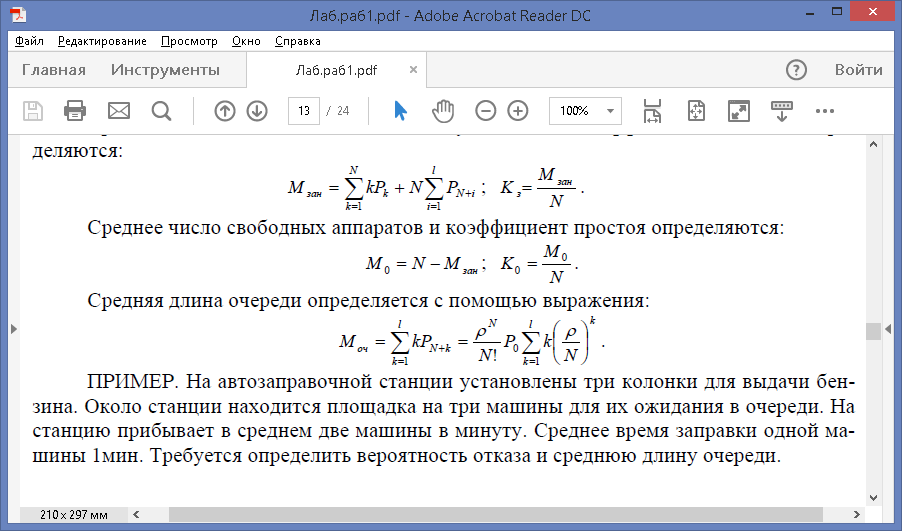
Средняя длина очереди определяется с помощью выражения:
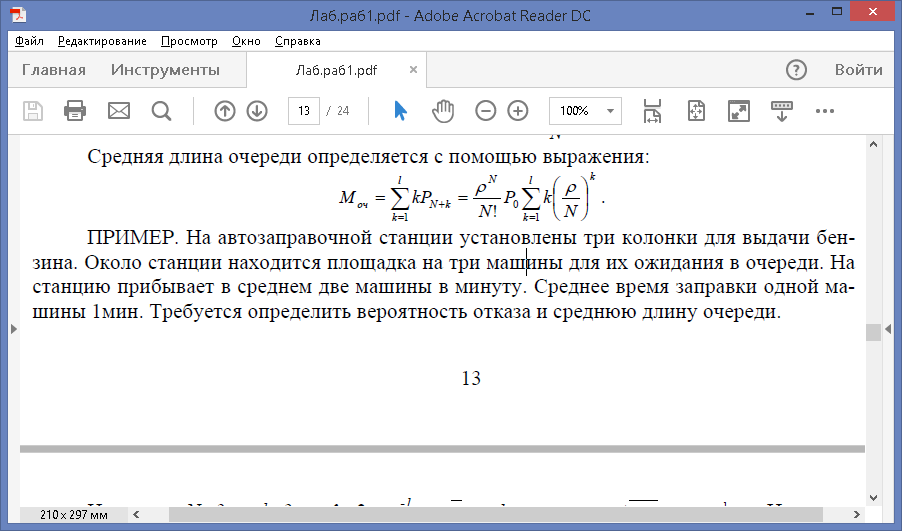
ПРИМЕР. На автозаправочной станции установлены три колонки для выдачи бензина. Около станции находится площадка на три машины для их ожидания в очереди. На станцию прибывает в среднем две машины в минуту. Среднее время заправки одной машины 1мин. Требуется определить вероятность отказа и среднюю длину очереди.
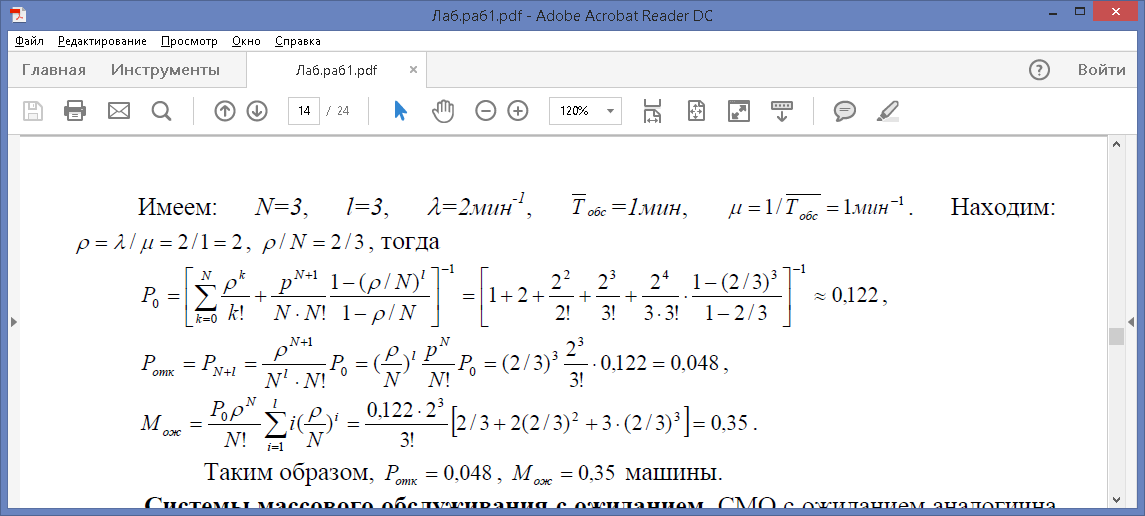
Таким образом, Pотк = 0,048, Мож = 0,35машины.
Системы массового обслуживания с ожиданием.СМО с ожиданием аналогична системе массового обслуживания с ограниченной длиной очереди при условии, что граница очереди отодвигается в бесконечность. Вероятность состояний СМО с ожиданием находят по формулам:
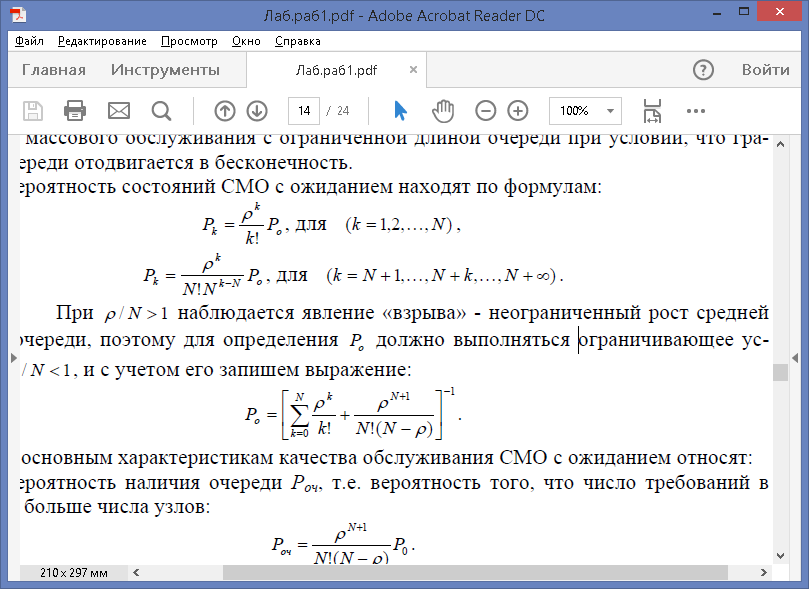
При ρ / N > 1 наблюдается явление «взрыва» - неограниченный рост средней
длины очереди, поэтому для определения P0должно выполняться ограничивающее условие ρ / N < 1, и с учетом его запишем выражение:
К основным характеристикам качества обслуживания СМО с ожиданием относят:
Вероятность наличия очереди Pоч, т.е. вероятность того, что число требований в
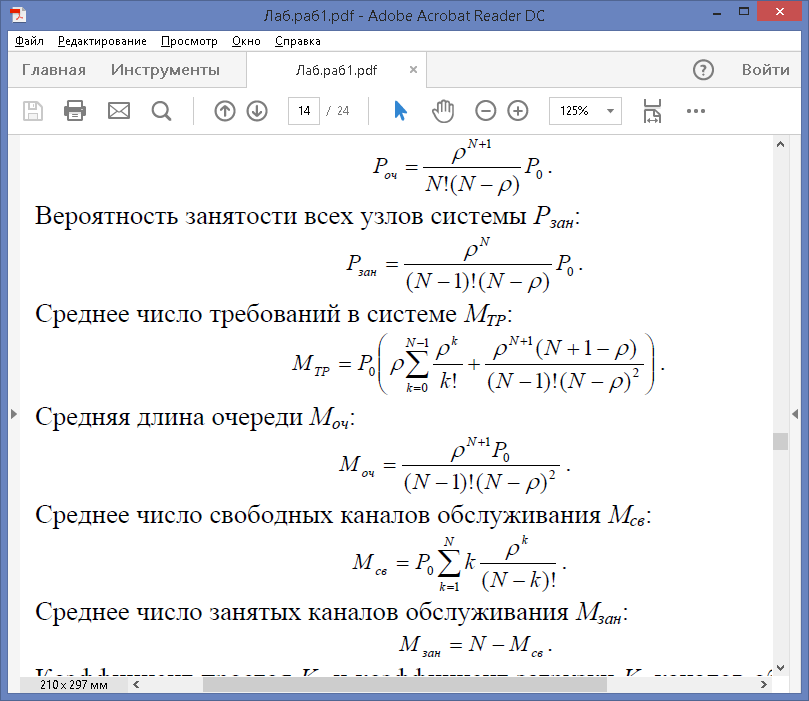системе больше числа узлов:
Коэффициент простоя K0 и коэффициент загрузки K3каналов обслуживания системы:
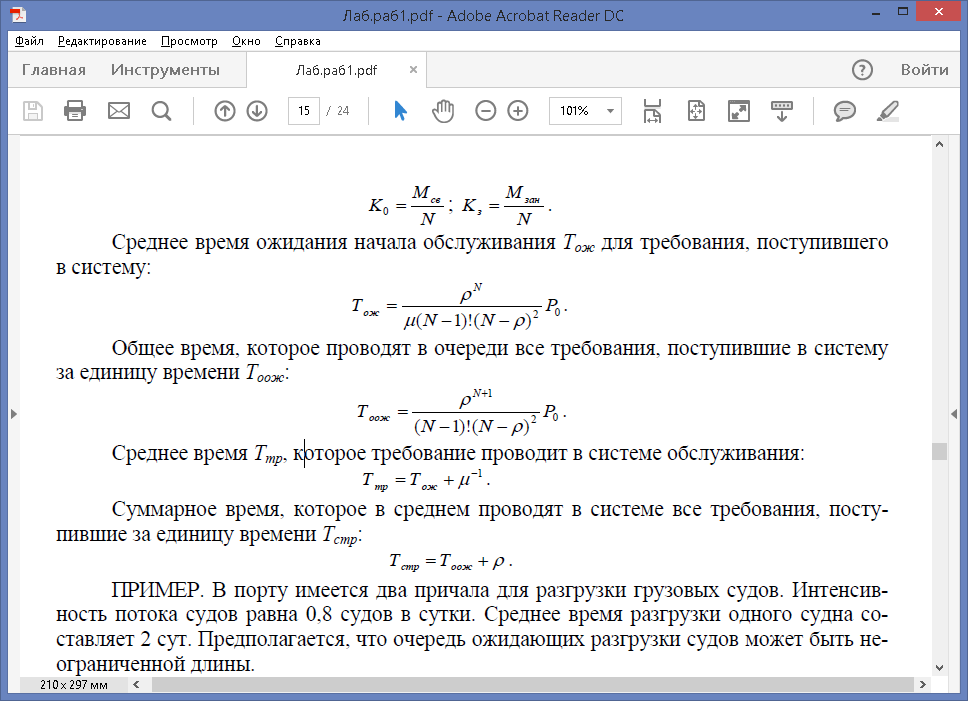
ПРИМЕР. В порту имеется два причала для разгрузки грузовых судов. Интенсив-
ность потока судов равна 0,8 судов в сутки. Среднее время разгрузки одного судна составляет 2 сут. Предполагается, что очередь ожидающих разгрузки судов может быть неограниченной длины.
Найти среднее время пребывания судна в порту.
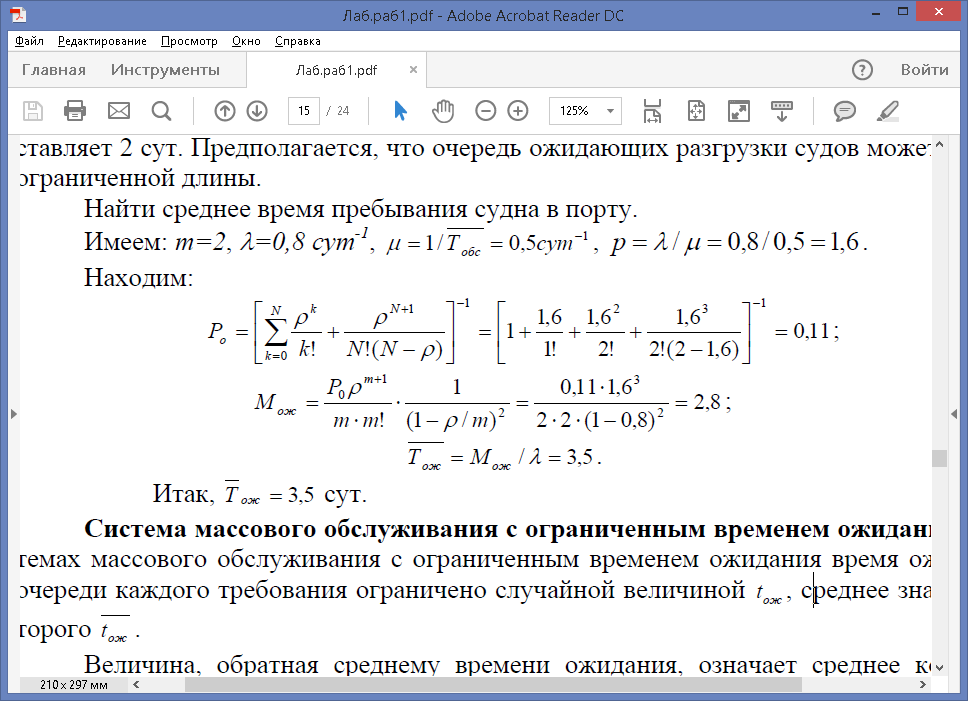
Система массового обслуживания с ограниченным временем ожидания. В системах массового обслуживания с ограниченным временем ожидания время ожидания в очереди каждого требования ограничено случайной величиной tож, среднее значение которого
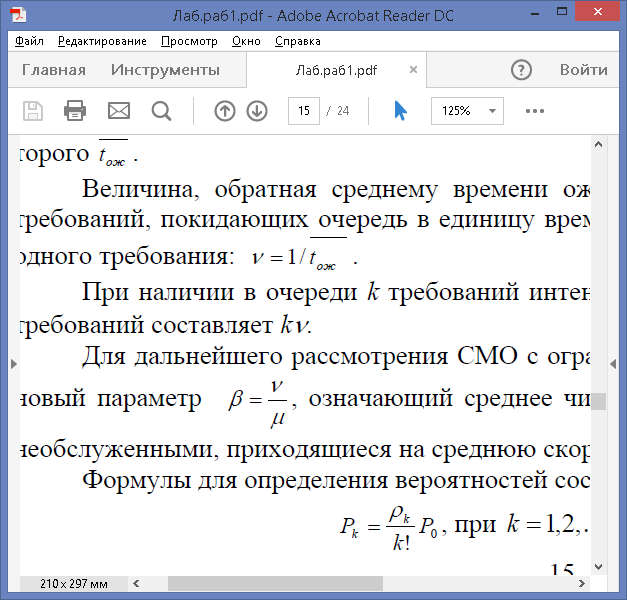
Величина, обратная среднему времени ожидания, означает среднее количество требований, покидающих очередь в единицу времени, вызванное появлением в очереди одного требования: v = 1/
При наличии в очереди k требований интенсивность потока покидающих очередь требований составляет kv.
Для дальнейшего рассмотрения СМО с ограниченным временем ожидания введем
новый параметр , означающий среднее число требований, покидающих
систему необслуженными, приходящиеся на среднюю скорость обслуживания
требований.
Формулы для определения вероятностей состояний такой системы имеют вид:
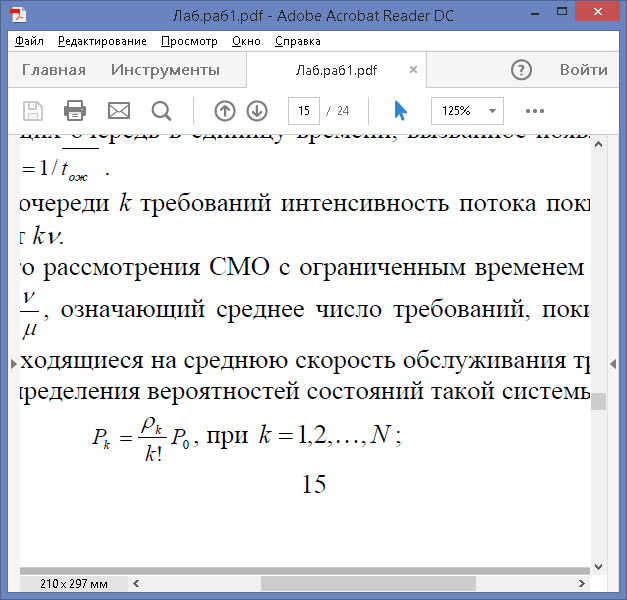
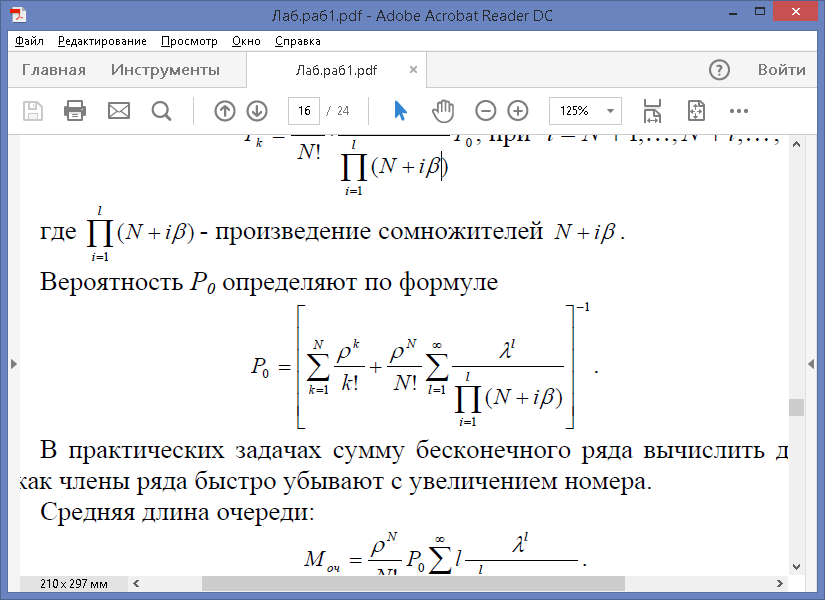
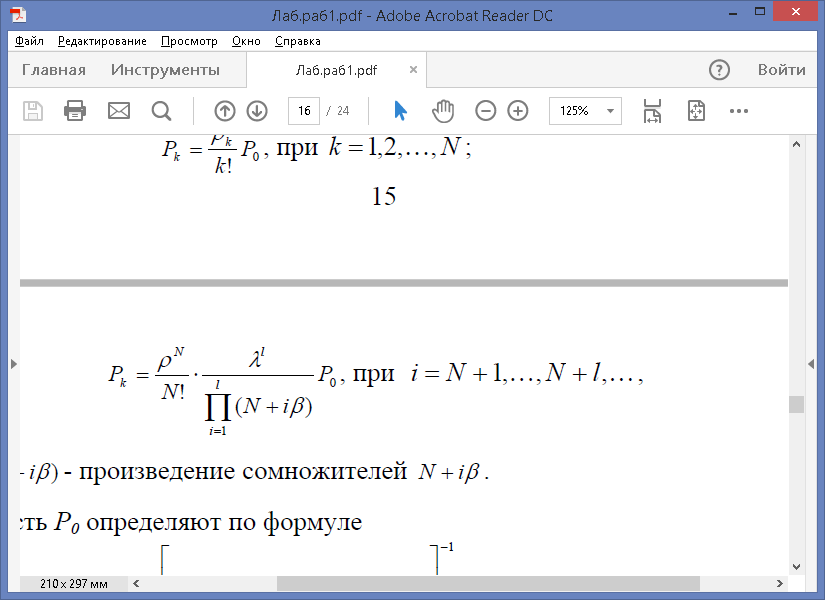
В практических задачах сумму бесконечного ряда вычислить достаточно просто, так как члены ряда быстро убывают с увеличением номера.
Средняя длина очереди:
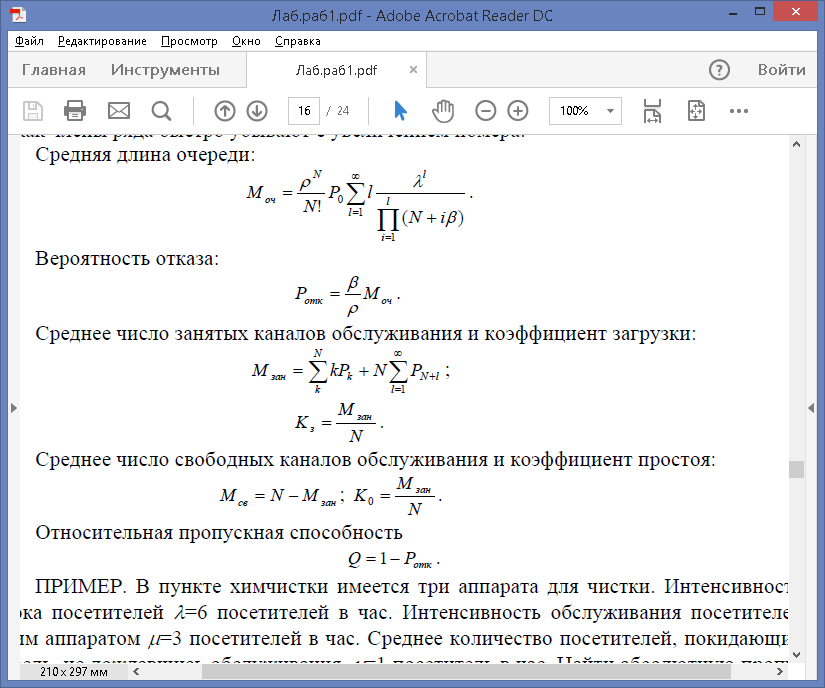
Вероятность отказа:
Среднее число занятых каналов обслуживания и коэффициент загрузки:
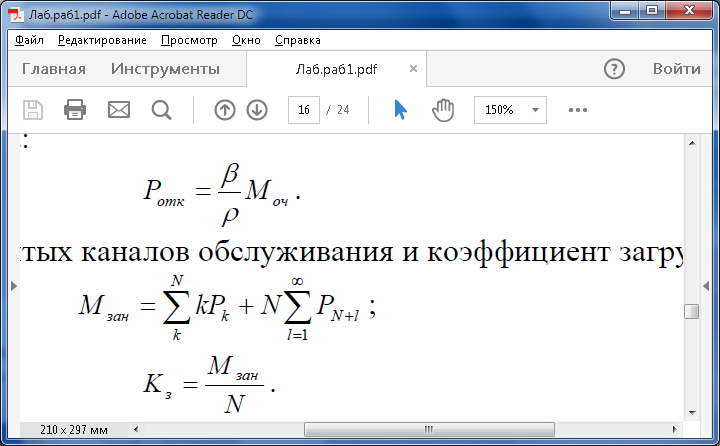
Среднее число свободных каналов обслуживания и коэффициент простоя:
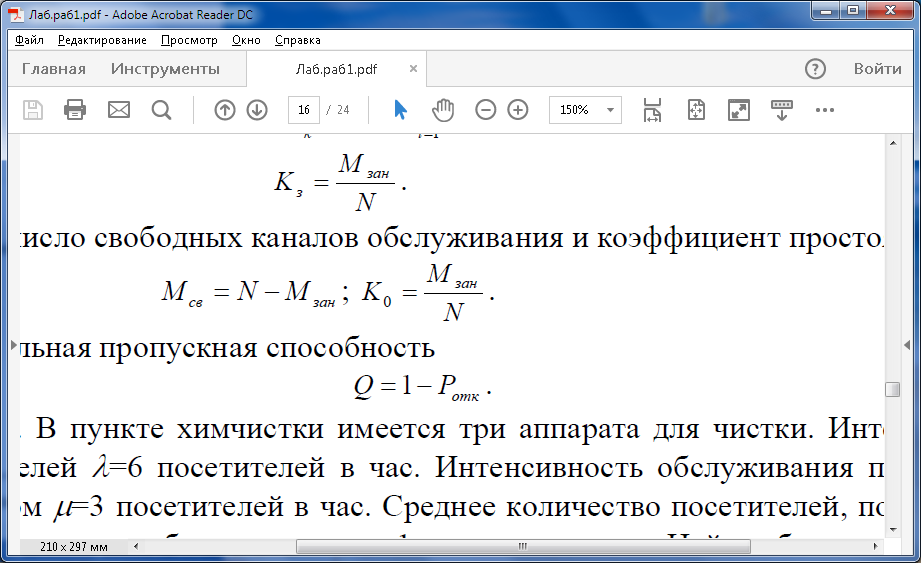
Относительная пропускная способность:
ПРИМЕР. В пункте химчистки имеется три аппарата для чистки. Интенсивность
потока посетителей λ=6 посетителей в час. Интенсивность обслуживания посетителей одним аппаратом μ=3 посетителей в час. Среднее количество посетителей, покидающих очередь, не дождавшись обслуживания, ν=1 посетитель
в час. Найти абсолютную пропускную способность пункта.
Имеем: m=З, λ=6, μ=3, ν=1. Находим: р = λ /μ = 6 / 3 = 2 ,
Вероятность занятости всех приборов равна Рзан = 1 – Р0 = 0,87. Тогда абсолютная пропускная способность может быть получена как произведение:
А = NРзан= 3 • 0,87 = 2,61. Таким образом, А = 2,61 посетителя в час.
Замкнутые системы массового обслуживания. В замкнутых системах массового обслуживания источник требований находится внутри системы, и интенсивность потока требований зависит от состояния самой системы.
Чаще всего потоком требований в такой системе является поток неисправностей от некоторой группы работающих устройств. Пусть имеется m работающих устройств, которые могут выходить из строя за счет неисправностей. Имеется также N приборов (каналов) обслуживания этих требований. В качестве таких каналов могут выступать и люди. Обычно предполагают, что N < m.
Обозначим через S0 состояние, при котором все устройства работают, а приборы обслуживания не заняты; S1 - состояние, при котором одно устройство вышло из строя и обслуживается одним прибором обслуживания; SN — N устройств не работают и все приборы заняты обслуживанием; Sm - все устройства не работают, из них N обслуживаются и m - N и ждут обслуживания.
Вероятности состояний замкнутой системы определяются следующими зависимостями:
Средняя длина очереди:
Коэффициент простоя требований в СМО:
Среднее число требований в СМО:
Среднее число свободных каналов и коэффициент простоя каналов K0 :
Вероятность занятости каналов обслуживания:
Абсолютная пропускная способность:
ПРИМЕР. Рабочий обслуживает группу из трех станков. Каждый станок останавливается в среднем два раза в час. Процесс наладки занимает в среднем 10 мин. Определить абсолютную пропускную способность наладки рабочим станков.
Имеем: n=1, m=3, λ=2, Тобс=1/6, μ=6. Находим: ρ = λ /μ = 1/ 3 ,
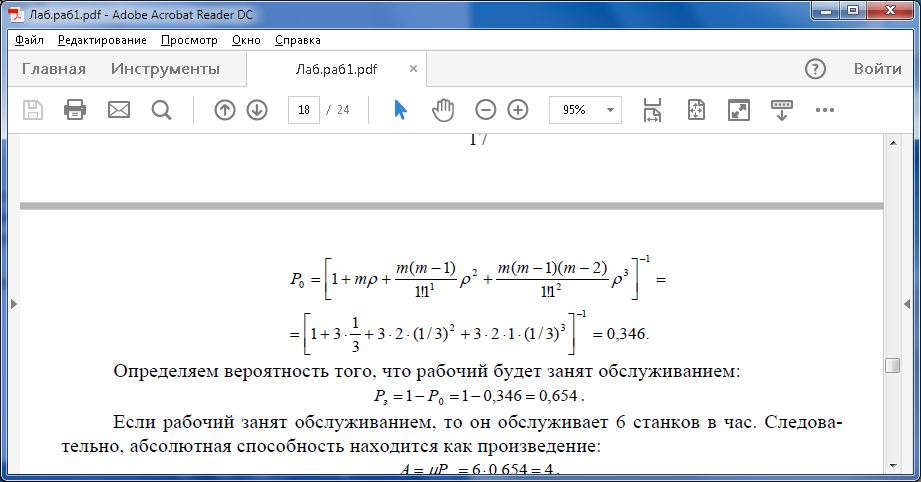
Определяем вероятность того, что рабочий будет занят обслуживанием:
Если рабочий занят обслуживанием, то он обслуживает 6 станков в час. Следовательно, абсолютная способность находится как произведение:
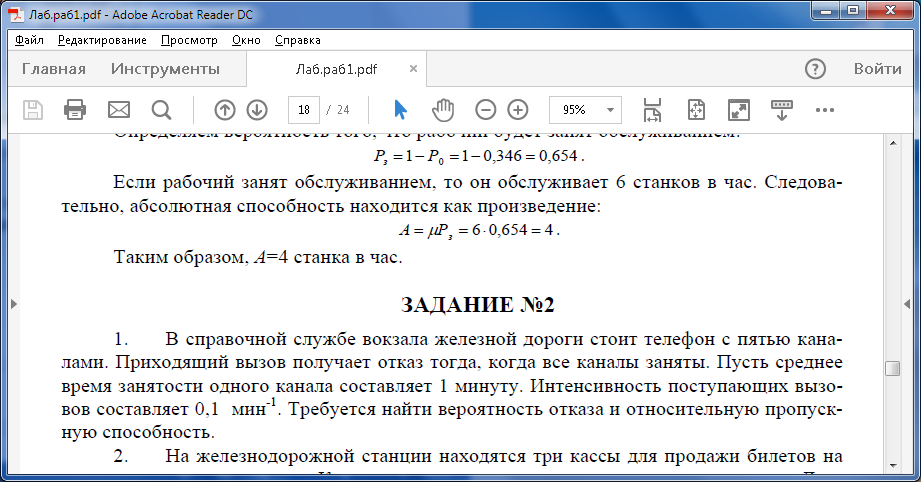
ЗАДАНИЕ
1. В справочной службе вокзала железной дороги стоит телефон с пятью каналами. Приходящий вызов получает отказ тогда, когда все каналы заняты. Пусть среднее время занятости одного канала составляет 1 минуту. Интенсивность поступающих вызовов составляет 0,1 мин-1. Требуется найти вероятность отказа и относительную пропускную способность.
2. На железнодорожной станции находятся три кассы для продажи билетов на поезда дальнего следования. Когда все кассы заняты, пассажиры встают в очередь. Длина очереди не может превышать 50 человек. Среднее время обслуживания в одной кассе составляет 5 минут. Пассажиры прибывают на станцию для покупки билетов в среднем по два человека в минуту. Найти вероятность отказа и общее количество человек (требований), находящихся в системе.
3. Для условия задачи 1 найти вероятность обслуживания вызова, а также вероятность поступления одного вызова.
4. На железнодорожной станции имеется пять путей для обслуживания прибывающих железнодорожных составов. Интенсивность прибытия железнодорожных составов равна 15 составов в час. Среднее время обслуживания одного состава 20 минут. Предполагается, что очередь ожидающих обслуживания поездов может быть неограниченной длины. Найти вероятность занятости всех пяти путей железнодорожной станции и среднее время обслуживания состава.
5. Программист обслуживает вычислительный центр из 50 вычислительных машин (ВМ). В среднем ВМ дает сбой 0,05 час-1. Процесс наладки занимает в среднем 45 минут. Требуется определить абсолютную пропускную способность наладки ВМ программистом.
6. В локомотивном депо обслуживается 100000 железнодорожных вагонов. Каждый вагон в среднем подлежит ремонту один раз в два года. На ремонт вагона затрачивается в среднем 5 дней. Найти вероятность того, что депо занято обслуживанием вагонов.
7. Сервис-центр занимается посреднической деятельностью по продаже железнодорожных билетов и осуществляет часть своей деятельности по 3 телефонным линиям. В среднем в сервис-центр поступает 75 звонков в час. Среднее время обслуживания каждого звонка составляет 2 минуты. Определить вероятность того, что ни один канал не занят, а также вероятность отказ.
8. Преподаватель производит прием экзамена у группы студентов из 23 человек, пришедших в течение одной минуты. Время приема экзамена у одного студента в среднем составляет 20 мин. Студенты, ждущие приема экзамена, находятся в очереди. Определить среднее время ожидания студентом приема экзамена.
9. Для условия задачи 7 определить вероятность занятости одного и двух каналов телефонной линии.
10. В вагоне-ресторане интенсивность обслуживания клиентов в среднем составляет 20 человек в час. Обслуживанием клиентов занимаются два официанта, при этом среднее время обслуживания одного клиента составляет 10 минут. Среднее количество клиентов, покинувших очередь, не дождавшихся обслуживания, составляет 2 человека в час. Определить абсолютную пропускную способность вагона-ресторана.
11. Для условия задачи 7 определить абсолютную пропускную способность сервисного центра.
12. В читальный зал государственной библиотеки, которая имеет 30 посадочных мест, приходят посетители с интенсивностью 20 человек в час. Время пребывания каждого посетителя в среднем составляет 2 часа. Определить вероятность отказа посетителю в читальном зале и среднее число занятых посадочных мест.
13. Абонентский отдел библиотеки обслуживают 3 библиотекаря. Время обслуживания одним библиотекарем читателя в среднем составляет 5 минут. Интенсивность посещения читателями библиотеки составляет 4 человека в минуту. Если в момент прихода читателя все библиотекари заняты, то он встает в очередь. Требуется определить среднее число читателей, ожидающих начала обслуживания и время их пребывания в очереди.
14. Поток заданий в 4-процессорном компьютере является простейшим с интенсивностью 1000 заданий в минуту. Среднее время обработки задания каждым процессором составляет 3 секунды. Если при поступлении задания все процессоры заняты, то задание помещается в очередь (очередь не ограничена). Требуется определить среднюю длину очереди и среднее число занятых процессоров.
15. В компьютерном классе установлен один принтер, скорость печати которого в среднем составляет 2 страницы в минуту. Печать начинается сразу после поступления файла на порт принтера. Среднее время между поступлениями файлов на принтер составляет 1 минуту. Если в момент поступления файла на печать принтер занят, то задания выстраиваются в неограниченную очередь. Требуется определить среднюю длину очереди и общее время пребывания файлов в очереди, если каждый файл в среднем содержит по 5 страниц.
16. На базу данных (БД) сервера железной дороги поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки предыдущего запроса, становится в очередь. Определить вероятность наличия очереди и суммарное время, которое проведут запросы до обслуживания.
17. На железнодорожной станции расположена гостиница, в которой имеется 20 мест. Посетитель в случае занятости мест уходит в другую гостиницу. Среднее время снятия гостиницы клиентом составляет 8 часов. Интенсивность потока поступления клиентов составляет 5 человек в час. Определить вероятность отказа и абсолютную пропускную способность данной гостиницы.
18. На телефонной станции железной дороги имеются три линии. Вызов, поступивший, когда все линии заняты, получает отказ. Поток вызовов является пуассоновским с интенсивностью 0,5 вызовов в минуту. Время обслуживания распределено по экспоненциальному закону и в среднем продолжительность разговора составляет 3 минуты. Найти вероятность отказа, относительную и абсолютную пропускные способности и долю свободного времени, приходящегося в среднем на каждую линию.
19. Четырехканальный концентратор имеет буфер емкостью 10 Мб. Пакеты данных поступают на концентратор с интенсивностью 51 пакетов в секунду. Пакеты, поступившие в момент, когда заняты все каналы, выстраиваются в очередь в буфере обмена, если он занят - получают отказ. Средняя скорость одного канала 256 Кб в секунду. Определить абсолютную пропускную способность канала концентратора при среднем размере пакета 2 Кб.
20. Два рабочих обслуживают группу из четырех станков. Остановка рабочего станка происходит в среднем через 30 минут. Время работы и время наладки распределено по экспоненциальному закону. Найти среднюю долю свободного времени для каждого рабочего и среднее время работы станка.
21. Для условия задачи 19 определить вероятность отказа передачи пакета и среднее число свободных каналов концентратора, если средний размер сообщения составляет 5 Кб.
22. Рассмотрим две рядом стоящие телефонные кабины, общая очередь перед которыми не бывает более трех человек («лишние» уходят к другим кабинам). Поток людей, желающих позвонить по телефону, является простейшим и имеет интенсивность 15 человек в час. Время, проводимое людьми в кабине, распределено по экспоненциальному закону и составляет в среднем 3 минуты. Найти среднюю долю времени, когда свободна одна кабина; вероятность того, что человеку придется искать другую кабину.
23. Для условия задачи 20 найти заданные характеристики системы, в которой два рабочих всегда обслуживают станок вместе, причем с двойной интенсивностью.
24. В буфете железнодорожной станции обслуживают клиентов два продавца. Интенсивность обслуживания одним продавцом составляет 0,5 человека в минуту. Посетители приходят в буфет со средним интервалом в 1 минуту. Если в момент прихода клиента все продавцы заняты, клиент встает в очередь, которая не может превышать 5 человек. Посетитель, не попавший в очередь, уходит в другой буфет. Определить вероятность отказа посетителю в обслуживании и среднее время ожидания в очереди.
25. Железнодорожный пропускной таможенный пункт состоит из трех линий досмотра. Время досмотра одного железнодорожного состава на линии досмотра в среднем составляет 4 часа. Интенсивность прибывающих составов составляет 2 состава в час. В случае занятости всех линий досмотра прибывший состав ставится на запасной путь. Определить абсолютную пропускную способность таможенного пункта и среднее время простоя линий досмотра.
26. Железнодорожная сортировочная горка, на которую подается простейший поток составов с интенсивностью 2 состава в час, представляет собой СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со средним значением времени 20 мин. Найти среднее число составов в очереди, среднее время пребывания состава в СМО, среднее время пребывания состава в очереди.
27. Автозаправочная станция (АЗС) имеет две колонки. Площадка возле нее допускает одновременное ожидание не более четырех машин. Поток машин, прибывающий на станцию, простейший с интенсивностью 1 машина в минуту. Время обслуживания автомашины распределено по показательному закону со средним значением 2 минуты.
Найти для АЗС финальные вероятности состояния для 1, 2,3 и 4-х машин, абсолютную пропускную способность и вероятность отказа в обслуживании.
28. Имеется двухканальная простейшая СМО с отказами. На ее вход поступает поток заявок с интенсивностью 4 заявки в час. Среднее время обслуживания одной заявки 0,8 ч. Каждая обслуженная заявка приносит доход в 4 рубля. Содержание каждого канала обходится 2 руб. в час. Решить: выгодно или не выгодно в экономическом отношении увеличить число каналов СМО до трех, если доход от заявок находится из соотношения D=Ac, где с - доход от обслуженной заявки, А - абсолютная пропускная способность СМО.
29. В зубоврачебном кабинете три кресла, а в коридоре имеются три стула для ожидания приема. Поток клиентов распределен по простейшему закону с интенсивностью 12 клиентов в час. Время обслуживания клиента распределено показательно со средним значением 20 минут. Если все три стула в коридоре заняты, клиенты в очередь не становятся. Определить среднее число клиентов, обслуживаемых кабинетом за час, среднюю долю обслуженных клиентов из числа пришедших и среднее время, которое клиент проведет в коридоре и в кабинете.
30. Билетную кассу с одним окошком представим, как СМО с неограниченной очередью. Касса продает билеты в пункты А и В; пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 минут, а в пункт В - двое за 20 минут. Поток пассажиров можно считать простейшим. Кассир в среднем обслуживает трех пассажиров за 10 минут. Время обслуживания распределено по показательному закону. Установить, существуют ли финальные вероятности состояний СМО, и если да - вычислить первые три из них. Найти среднее число заявок в СМО, среднее время пребывания заявки в системе и среднее число заявок в очереди.
31. Железнодорожная касса имеет два окошка, в каждом из которых продаются билеты в два пункта: Москву и Петербург. Продажа билетов в оба направления одинакова по интенсивности, которая равна 0,45 пассажиров в минуту. Среднее время обслуживания пассажира (продажи ему билета) 2 минуты. Поступило рационализаторское предложение: для уменьшения очередей (в интересах пассажиров) сделать обе кассы специализированными. В первой продавать билеты только в Петербург, а во второй - только в Москву. Считать все потоки событий простейшими. Требуется проверить разумность этого предложения.
32. Рассматривается простейшая двухканальная СМО с «нетерпеливыми» заявками. Интенсивность потока заявок 3 заявки в час; среднее время обслуживания одной заявки 1 час; средний срок, в течение которого заявка «терпеливо» стоит в очереди, равен 0,5 ч. Подсчитать финальные вероятности состояний, ограничиваясь теми, которые не меньше 0,001. Найти относительную и абсолютную пропускные способности.
33. Ремонтный мастер обслуживает группу из 8-ми кассовых автоматов по продаже билетов в пригородные поезда. Наблюдения показали, что в среднем автомат требует вмешательства мастера раз в 2 ч. Поток требований на ремонт - простейший. Устранение неполадок в автомате занимает в среднем 6 мин, причем время ремонта есть величина случайная, распределенная по показательному закону. Определить коэффициент простоя мастера и среднюю длину очереди автоматов на обслуживание.
34. АТС имеет 6 линий связи. Поток требований на переговоры - простейший с интенсивностью один вызов в минуту. Среднее время переговоров - 3 мин. Закон распределения времени показательный. Определить вероятность отказа и коэффициент загрузки линий связи.
35. На станции метро 5 кассовых аппаратов. Из наблюдений установили, что к этим пяти аппаратам подходят в среднем 60 человек в минуту. Время обслуживания будем считать распределенным по показательному закону, со средним временем обслуживания 4 сек. Найти вероятность того, что все аппараты свободны и среднее число людей, находящихся у аппаратов.
36. В камеру хранения вокзала, состоящую из 5-ти секций, поступает простейший поток требований в среднем 2 требования в минуту. Время обслуживания распределено по показательному закону и составляет в среднем 2 минуты. Время ожидания в очереди составляет в среднем 4 минуты и распределено по показательному закону. Определить среднюю длину очереди, среднее число занятых секций и относительную пропускную способность системы.
37. В железнодорожной поликлинике в кабинете флюорографии проходят прием в среднем 2 человека в минуту. Время приема распределено по показательному закону. Поток посетителей простейший с интенсивностью 5 человек в минуту. Очередь посетителей, ожидающих приема, не ограничена. Определить среднюю длину очереди и абсолютную пропускную способность кабинета флюорографии.
38. Железнодорожная сортировочная горка, на которую подаются простейший поток составов с интенсивностью 2 состава в час, представляет собой СМО с неограниченной очередью. Время обслуживания (роспуска) состава на горке имеет показательное распределение со средним значением времени 15 мин. Найти среднее число составов в очереди, среднее время пребывания состава в очереди, а также абсолютную пропускную способность сортировочной горки.
1. На базу данных (БД) сервера железной дороги поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки предыдущего запроса, становится в очередь. Определить вероятность наличия очереди, вероятность отсутствия запроса и коэффициент загрузки сервера.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4
ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
ЗАДАНИЕ
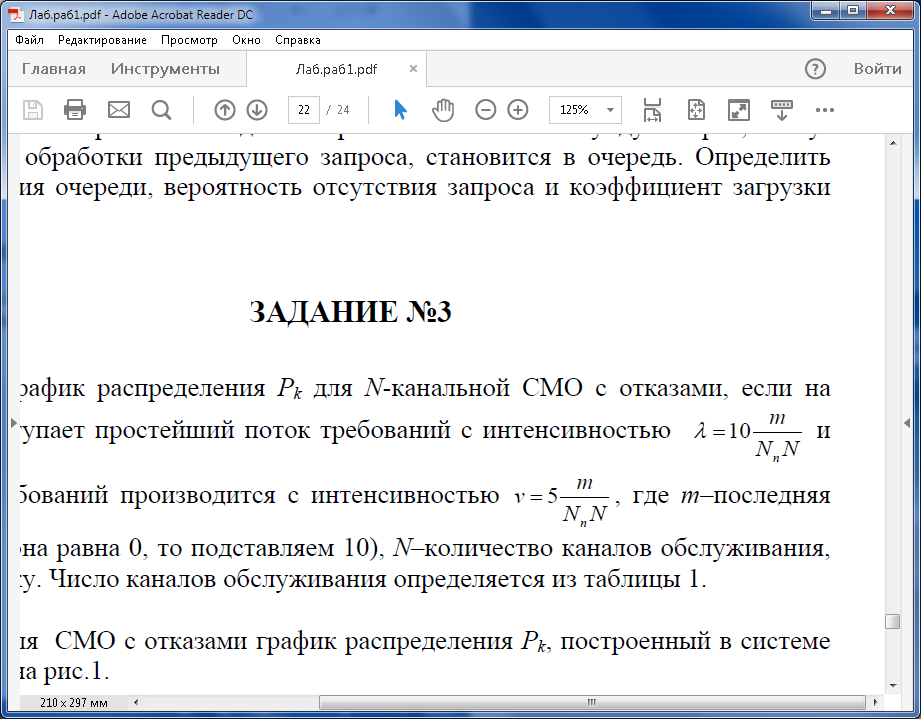Построить график распределения Pk для N-канальной СМО с отказами, если на вход системы поступает простейший поток требований с интенсивностью
И обслуживание требований производится с интенсивностью где m–последняя
цифра года (если она равна 0, то подставляем 10), N–количество каналов обслуживания,
Nn –номер по списку. Число каналов обслуживания определяется из таблицы 1.
ПРИМЕР. Для СМО с отказами график распределения Pk, построенный в системе
MathCad, показан на рис.1.
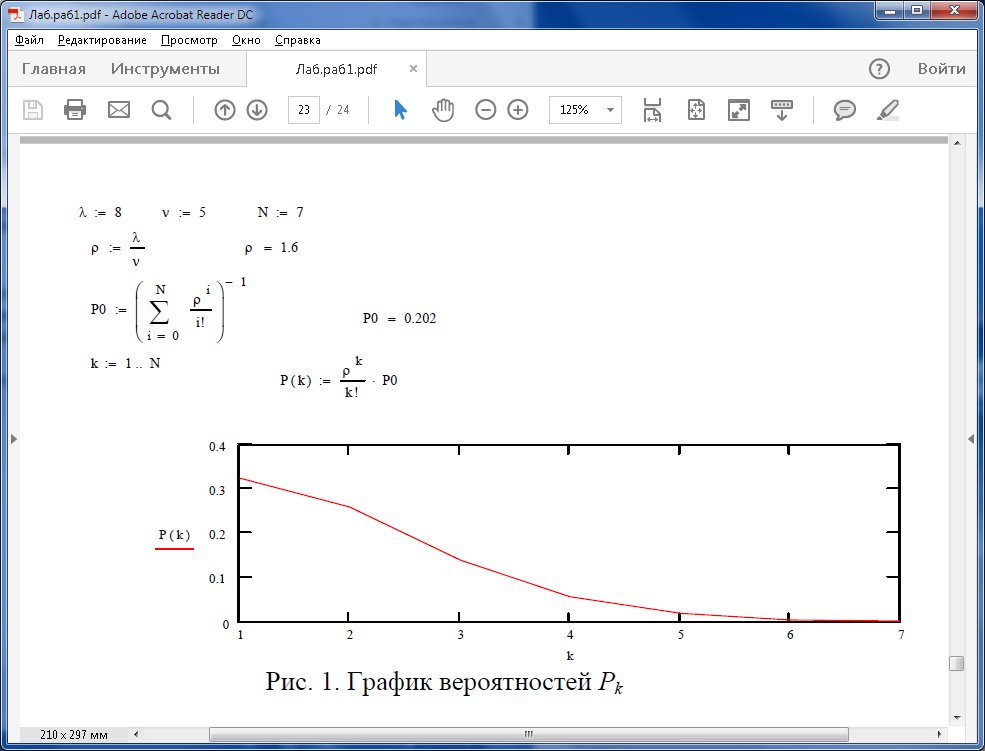
Определить характеристики качества обслуживания для СМО с отказами:
1. Вероятность отказа Ротк.
2. Среднее число занятых узлов Мзан.
3. Среднее число свободных узлов Мсв.
4. Относительную пропускную способность Q.
5. Абсолютную пропускную способность А.
6. Коэффициент занятости узлов Кз.
ЗАДАНИЕ №4
Построить график вероятности состояний Pk, для N-канальной СМО с ожиданием,
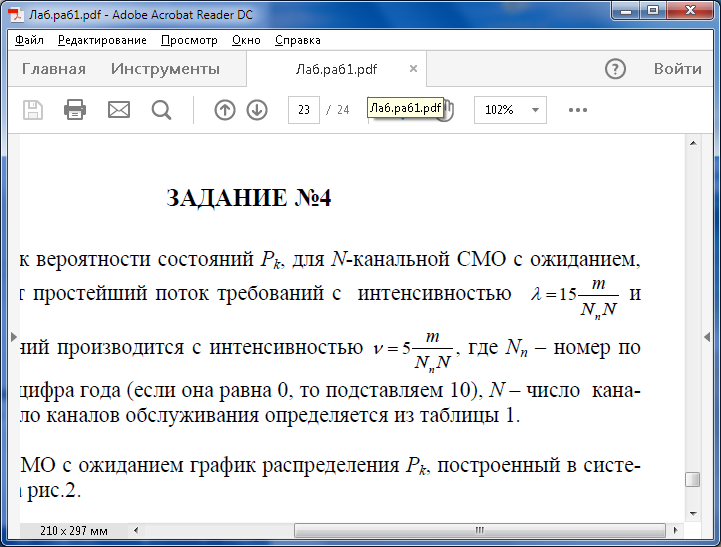
если на вход поступает простейший поток требований с интенсивностью
и обслуживание требований производится с интенсивностью где Nп – номер
по списку, m – последняя цифра года (если она равна 0, то подставляем 10), N – число каналов обслуживания. Число каналов обслуживания определяется из таблицы 1.
ПРИМЕР. Для СМО с ожиданием график распределения Pk, построенный в систе-
ме MathCad, показан на рис.2.
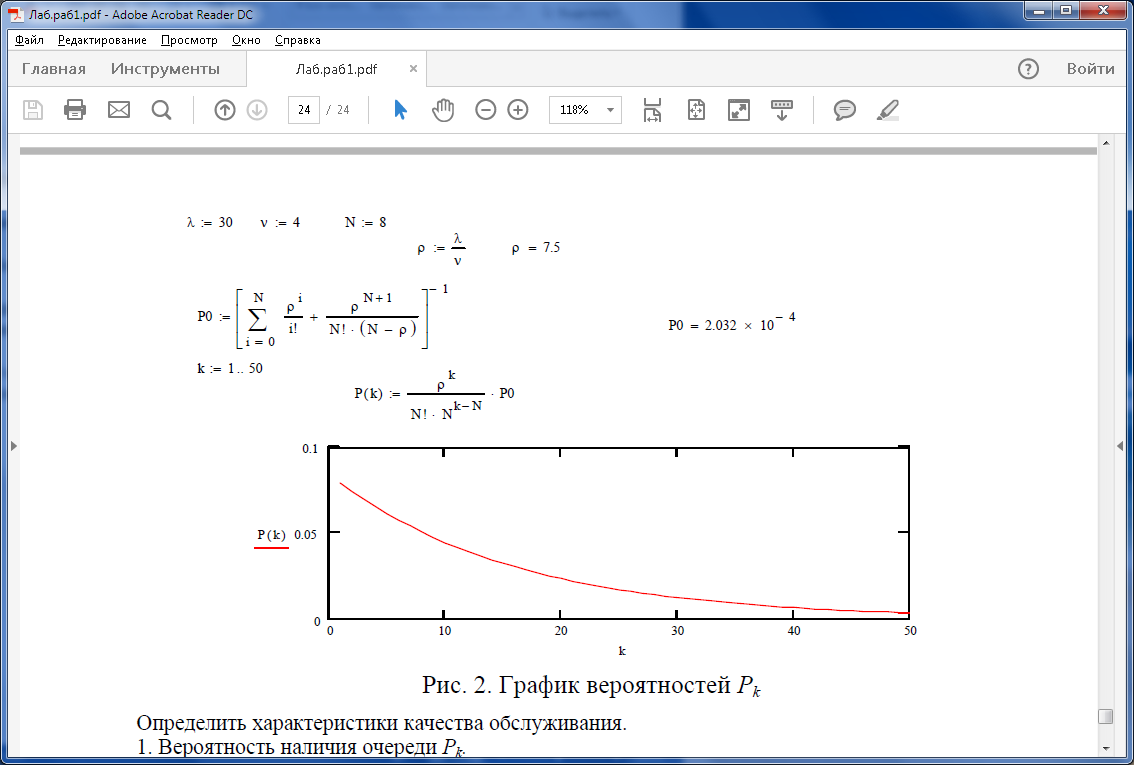
Определить характеристики качества обслуживания.
1. Вероятность наличия очереди Pk.
2. Вероятность занятости всех узлов системы Pзан.
3. Среднее число требований в системе МТР.
4. Среднюю длину очереди Mоч.
5. Среднее число свободных узлов Мсв.
6. Среднее число занятых узлов Мзан.
7. Среднее время ожидания Тож.
8. Общее время пребывание требований в очереди за единицу времени Тоож.
9. Среднее время пребывания требования в системе Ттр.
10. Суммарное время, которое проводят все требования за единицу времени Тстр.
11. Абсолютную пропускную способность А.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Алехин М.Ю. и др. Применение теории массового обслуживания для решения производственных задач. – Л.: ЛКИ, 1989.
2. Бронштейн О.И., Духовный И.М. Модели приоритетного обслуживания в информационно-вычислительных системах. – М.: Наука, 1976.
3. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения.– М.: Наука, 1991.
4. Фомин Г.Ф. Системы и модели массового обслуживания в коммерческой деятельности:
Учеб. пособие. – М.: Финансы и статистика, 2000.
5. Математика для экономистов: В 6 т./ Под. ред. А.Ф. Тарасюка. – М.: ИНФРА – М, 2000. –(Серия «Высшее образование»). Т.6: Чернов В.П., Ивановский В.Б. Теория массового обслуживания.
6. Клейнрок Л. Теория массового обслуживания. /Пер. с англ. И.И. Грушко; ред. В.И. Нейман. – М.: Машиностроение, 1979. – 432 с., ил.
7. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – 2-е изд.,
перераб. и доп. - М.: Наука: Гл.ред. физ.-мат. лит., 1987. – 336 с.
8. Хугаев К.Д. Элементы теории массового обслуживания: Учеб. пособие. – Ленинград;
ЛИИЖТ, 1973. – 53 с.
9. Понттогофф Г. Теория массового обслуживания /Пер. с нем.; Под ред. Е.П. Нестерова. -М.: Транспорт, 1979. - 144 с.
Дата добавления: 2018-04-05; просмотров: 8884; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!