Порядок выполнения задания (1 уровень)
1. Решение уравнения графическим методом.
1.1. Проверим графически, что на заданном отрезке [a, b] есть корень уравнения f(x)= 0, т.е.
. (1)
Перепишем уравнение (1): 
Построим два графика 
(рис. 3.1)
| M |
| X* |
Рис. 3.1. Пересечение графиков
Графики пересекаются друг с другом в точкеМ. Абсцисса точки М (X*)–есть корень уравнения 
1.2.Если на заданном в условии отрезке графики не пересекаются, то это означает, что данный отрезок не содержит корня уравнения. В этом случае следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его.
2. Составление блок-схемы задачи табулирования.
2.1. Входные данные: a, b – границы отрезка, h- шаг.
Выходные данные: 11 пар значений (x, y).
| начало |
| a, b, h |
| x= a,b,h |
| y=f(x) |
| a, b, h |
| конец |
Рис. 3.2. Блок-схема алгоритма табулирования
3. Составление программы по блок-схеме из п.2.
3.1. Объявить переменные A, B, H, Y, Xодинарной точности вещественного типа (Single).
3.2. Запросить ввод исходных данных с клавиатуры (Console.WriteLine()).
3.3. Открыть цикл для вычисления значения функции Yдля аргумента X, изменяющегося от Aдо B с шагомH (ForX = AToВStepH).
3.4. В цикле вычислить и вывести на экран значение функции Y(X) и соответствующего аргумента X.
3.5. Закрыть цикл(NextX) и завершить программу.
4. Выполнить программу и выписать результаты в отчёт (по аналогии с рис. 3.3).
| x = 1 | y = - 0.5 | x = 1.6 | y = - 0.126 |
| x = 1.1 | y = - 0.425 | x = 1.7 | y = - 0.77 |
| x = 1.2 | y = - 0.356 | x = 1.8 | y = - 0.032 |
| x = 1.3 | y = - 0.292 | x = 1.9 | y = 1.08 E-02 |
| x = 1.4 | y = - 0.232 | x = 2 | y = 5.10 E-02 |
| x = 1.5 | y = - 0.177 |
Рис. 3.3. Результаты: 11 пар значений (x, y)
5. Из таблицы значений, полученной в п.4, найти и выписать отрезок, на котором функция f(x)меняет свой знак. В данном случае это отрезок [1.8, 1.9], т.к.f(1.8)<0, аf(1.9)>0.
6. На найденном отрезке [1.8, 1.9] запустить программу табулирования функции f(x)с шагом h =0.01.
7. Из полученных результатов найти и выписать две строки, где функция f(x)меняет знак:
x = 1.87 y = - 1.732Е-08 f(x) <0
x = 1.88 y= 2.474Е-03 f(x) >0
8. Вычислить середину выбранного отрезка [1.87, 1.88]: X1=(1.87+1.88)/2 = 1.875 и значение функции в корне X1 
(y=3.743E-04).
9. Выписать результаты: значение корня (X1), значение функции в корне (y(X1)).
Вывод: значение X1=1.875 является приближённым значением корня уравнения с точностью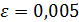 
.
Пояснения к выполнению задания второго уровня
Для реализации выхода из программы выполнить проверку длины найденного отрезка (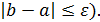 
Если это условие не выполняется, то программа должна запроситьграницы следующего отрезка, на котором функция имеет разные знаки на концах отрезка.Взятьграницы отрезка с экрана из результатов табулирования на предыдущем отрезке. Если условие выполняется, то необходимо в программе вычислить корень уравнения и значение функции в корне.
Пояснения к выполнению задания третьего уровня
Для поиска в программе нового отрезка табулирования выполнять проверку условия 
. Для выхода из программы сравнивать длину найденного отрезка с заданной точностью. Перед выходом из программы вычислить корень уравнения и значение функции в корне.
Таблица 3.1. Варианты заданий к лабораторной работе №3
| № вар. | Уравнение | Отрезок [а, b] | № вар. | Уравнение | Отрезок [а,b] |
| 1 | 
| [0;1] | 16 |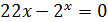 
| [0;1] |
| 2 | 
| [1;2] | 17 | 
| [3;4] |
| 3 | 
| [0.1;1.1] | 18 | 
| [-1;0] |
| 4 | 
| [0.1;1.1] | 19 | 
| [1;2] |
| 5 | 
| [2;3] | 20 | 
| [0.1;1.1] |
| 6 | 
| [0;1] | 21 | 
| [0;1] |
| 7 | 
| [-2;-1] | 22 | 
| [0;1] |
| 8 | 
| [0.1;1.1] | 23 | 
| [1;2] |
| 9 | 
| [0;1] | 24 |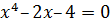 
| [1;2] |
| 10 | 
| [-0.5;0.5] | 25 | 
| [-1;0] |
| 11 |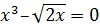 
| [0.1; 1.1] | 26 | 
| [2;3] |
| 12 | 
| [0.2;1.2] | 27 | 
| [0;1] |
| 13 | 
| [0.1; 1,1] | 28 | 
| [-0.5; 0.5] |
| 14 | 
| [0;1] | 29 | 
| [2; 3] |
| 15 | 
| [1;2] | 30 | 
| [0;1] |
ЛАБОРАТОРНАЯ РАБОТА №4
Тема: Одномерные массивы.
Цель работы: приобретение навыков разработки алгоритмов и программ по преобразованию одномерных массивов.
Варианты заданий лабораторной работы №4 приведены в таблицах 4.1, 4.2.
Задание (1 уровень)
1. Составить блок-схему алгоритма вычисления функцииY=f(X). Функцию f(X) взять из таблицы 4.1 в соответствии со своим вариантом.
2. Разработать программу вычисления элементов массива Yна основе элементов массива X, где Y=f(X).Массив X взять из таблицы 4.1 в соответствии со своим вариантом.
3. Выполнить программу, записав полученные результаты в отчёт.
Задание (2 уровень)
1. Составить блок-схему алгоритма вычисления наибольшего и наименьшего элементов в массиве Y, их порядковых номеров, а также суммы всех элементов массива Y.Массив Yполучить на основе элементов массива X, где:Y=f(X). Функцию f(X) взять из таблицы 4.1 в соответствии со своим вариантом.
2. На основе блок-схемы, составленной в п.1 разработать программу. Массив X взять из таблицы 4.1 в соответствии со своим вариантом.
3. Выполнить программу, записав полученные результаты в отчёт.
Задание (3 уровень)
1. Составить блок-схему алгоритма для задания, описанного в таблице 4.2 в соответствии со своим вариантом.
2. На основе блок-схемы, составленной в п.1 разработать программу.
3. Выполнить программу, записав полученные результаты в отчёт.
Пример:
Вычислить таблицу значений функции
Y= 
|
дляследующихзначений аргумента X:
X={-6.2; -0.8; 0.3; 0.5; -1.3; 4.1}.
Дата добавления: 2018-04-04; просмотров: 297; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!