Основная теорема алгебры комплексных чисел (Гаусса)
Теорема.Всякий многочлен с любыми числовыми коэффициентами, степень которого больше либо равна единице, имеет хотя бы один корень в поле комплексных чисел.
Эту теорему мы доказывать не будем.
Следствие 1. Многочлен f(x) с любыми числовыми коэффициентами разлагается на линейные множители вида x-α над полем комплексных чисел, причем такое разложение однозначно с точностью до порядка следования сомножителей.
◄ Применяя теорему, получим:
f(x) = (x-α1) f1(x) = (x-α1) (x-α2) f2(x)=…=a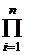 
(x-αi), a — коэффициент при старшей степени; П — произведение.►
Замечание 1. Это следствие решает задачу о разложении многочлена) на неприводимые множители над полем комплексных чисел.
Cледствие 2:Пусть f(x) — многочлен над полем вещественных чисел f(x) 
R[x]; α C(комплексное число). Если α — корень f(x), то и 
— корень f(x). Если α — корень кратности k, то и — корень кратности k ( α называют корнем кратности k многочлена, если f(x) можно представить в ви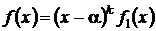де:
, где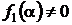 
.
Доказательство. Пусть
f(x) =an xn +…a0 R[x], тогда
………………..
f(α)=anαn+an-1 αn-1+…+a0 =0
_ _
Отсюда следует, что
an(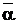 
)n + an-1( 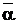)n-1 +…+ a0 
.
Пусть α — корень кратности k (α — комплексное число,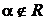 
), т.е. 
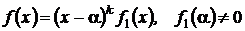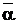, — корень какой-то кратности 
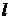, т.е.
f(x) = (x- )l f2(x).
Докажем, что k=l.
Будем доказывать от противного, т.е. полагаем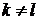 
, например, 
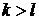. Заметим, что α — корень f2(x), причем α — корень кратности k. Положим
|
|
|
p(x)=(x-α) (x- 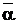)=x2 + px +q R[x]. Имеем
f(x)= (x-α)l(x-α)l q(x) = (x2+px+q)l q(x).
Отсюда следует, что q(x) — многочлен с действительными коэффициентами и q(α) = 0, ибо мы предположили, что k>l. Отсюда сразу же следует, что q( 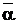)=0. А это противоречит тому, что 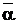— корень кратности l. Пришли к противоречию. Оно возникло из предположения, что k>l. Аналогично получим противоречие, если предположим, что k<l.►
Следствие 3: Пусть f(x) R[x] многочлен с действительными коэффициентами, f(x) можно представить в виде произведения его старшего коэффициента, линейных множителей вида (x-α), где α соответствует действительным корням многочлена, и множителей вида x2+px+q, соответствующих парам комплексно-сопряженных корней.
◄Cогласно следствию 1 f(x) можно представить в виде:
f(x) = a (x-α1)…(x-αk)(x-αk+1)(x-αk+1)…
Сначала запишем множители, соответствующие действительным корням, потом — множители, соответствующие парам комплексно-сопряженных корней.
Легко заметить, что многочлен (x-αk+1)(x- 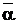k+1)=x2+p1x+q1 R[x] с действительными коэффициентами и так для каждой пары комплексно-сопряженных корней.
Замечание 2. Следствие 3 решает задачу о разложении на неприводимые над полем действительных чисел.
Формулы Виета. Кратные корни.
|
|
|
Формулы Виета дают связь между коэффициентами многочлена и его корнями (для приведенного уравнения, т.е. такого уравнения, у которого старший коэффициент равен единице).
Рассмотрим многочлен:
f(x)=xn + a1 xn-1 +…+an .
Пусть a1,…,an P — коэффициенты многочлена,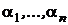 
— его корни. Можно записать (см. § 7, следствие 1):
f(x) = (x-α1)(x-α2)…(x-αn).
Чтобы получить xn-1 из каждой скобки надо взять x, за исключением одной скобки, из которой взят аi, чтобы получить xn-2 надо взять x из всех скобок, за исключением двух и т.д. Получим
a1 = ( α1+α 2+…+ αn )
a2 = α1α2+…+ (1)
…
an = (-1)nα1 …αn
Если мы домножим каждое равенство из (1) на (-1) в степени, равной индексу аi, то мы получим привычные нам формулы Виетта.
-a1 = α1+α2+…+αn
a2 = α1α2 +…+ (2)
……………..
(-1)n an = α1… αn
Кратные корни.
Пусть для f(x) = (x-α)k f 
(x) ; f (α)≠0, т.е. 
— корень кратности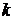 
.
Теорема 1. Если α — корень кратности k для многочлена, то α — корень кратности k-1 для его производной.
◄ Доказательство следует из теоремы о кратности неприводимых множителей (т.2, § 5). ►
|
|
|
Упражнение.Верно ли утверждение,обратное этой теореме?
ТЕМА 4. ГРУППА.КОЛЬЦО. ПОЛЕ.
Дата добавления: 2018-04-04; просмотров: 1171; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!