Вычислимые по Тьюрингу функции. Машина Тьюринга и Нормальные алгоритмы А.А
Машина Тьюринга и Нормальные алгоритмы А.А. Маркова
Машина Тьюринга (МТ)
Алан Тьюринг в 1936 году опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешений», которая наравне с работами Э.Поста и А.Чёрча лежит в основе теории алгоритмов. История создания этой работы связана с формулировкой Давидом Гильбертом на Международном конгрессе математиков в Париже в 1900 году неразрешенных математических проблем. Одной из таких проблем была задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» – нахождение общего метода для определения выполнимости данного высказывания на языке формальной логики.
Статья Тьюринга как раз и давала ответ на эту проблему – вторая проблема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки той задачи, по поводу которой она была написана.
«Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, то есть процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислимого процесса. Полученная модель вычислений, в которой каждый алгоритм разбивается на последовательность простых, элементарных шагов и была логической конструкцией, названной впоследствии машиной Тьюринга». (Джон Хопкрофт)
|
|
|
МТ есть математическая (воображаемая) машина. Так же как и другие математические понятия, понятие МТ отражает объективную реальность, моделирует некие реальные процессы.
Тьюринг предпринял попытку смоделировать действия математика (или другого человека), осуществляющего некую умственную деятельность. Такой человек, находясь в определенном «умонастроении» (состоянии), просматривает некий текст. Затем он вносит в этот текст какие-то изменения, проникается новым «умонастроением» и переходит к просмотру последующих записей.
МТ действует примерно также. Ее удобно представлять в виде автоматически работающего устройства. В каждый дискретный момент времени устройство, находясь в некотором состоянии, обозревает содержимое одной ячейки протягиваемой через устройство ленты и делает шаг, заключающийся в том, что устройство изменяет (или оставляет без изменения) содержимое обозреваемой ячейки, переходит в новое состояние, и переходит к обозрению следующей ячейки – справа или слева. Причем шаг осуществляется на основании предписанной команды. Совокупность всех команд представляет собой программу МТ.
|
|
|
МТ располагает конечным числом знаков, образующих внешний алфавит А = {а0, а1, … , ап}. В каждую ячейку обозреваемой ленты в каждый дискретный момент времени может быть записан только один символ из алфавита А. Удобно считать, что среди букв внешнего алфавита А имеется так называемая «пустая» буква, которая записывается в пустую ячейку ленты. Как правило, символом пустой ячейки являются буквы а0, е или 0 (если не используется десятичный алфавит). Лента предполагается неограниченной в обе стороны, но в каждый момент времени на ней записано конечное число непустых букв.
В каждый момент времени МТ способна находиться в одном состоянии из конечного числа внутренних состояний Q = {q0, q1, … , qm}. Среди состояний всегда имеются два: q1 – начальное состояние (находясь в этом состоянии, МТ начинает работу) и q0 – заключительное или состояние останова (попав в него, МТ прекращает работу).
Работа МТ определяется программой или функциональной схемой или функцией переходов d, которая задается отображением пары из декартова произведения множеств Q х А (множество упорядоченных пар, первый элемент которых берется из множества Q, а второй элемент – из множества А) в тройку из декартова произведения Q х А х Х, где Х = {П, Л, С} – множество переходов МТ по ленте (П – переход вправо на одну ячейку, Л – переход влево на одну ячейку, С – МТ остается на месте (в программе часто этот символ не пишется)).
|
|
|
Решаемая проблема задается путем записи конечного числа символов из множества А на ленту.
| … | е | е | а1 | а2 | а3 | е | е | … |
Работа МТ: Находясь в какой-либо момент времени в незаключительном состоянии (qi ≠ q0), МТ совершает шаг, который полностью определяется ее текущим состоянием qi и символом аj, воспринимаемым ею в данный момент на ленте. При этом содержание шага регламентировано соответствующей командой T(i, j): qiаj→ qkаlX, Х = {П, Л, С}. Шаг заключается в том, что:
1. содержимое аj обозреваемой на ленте ячейки стирается и на его место записывается символ аl, который может совпадать с аj;
2. машина переходит в новое состояние qk, которое также может совпадать с предыдущим состоянием qi;
3. машина переходит к обозрению следующей правой ячейки, если Х = П, или следующей левой ячейки, если Х = Л или остается на месте, если Х = С (или нет никакого символа).
|
|
|
В следующий момент времени, если qk ≠ q0, машина делает шаг, регламентированный соответствующей командой T(k; l).
Поскольку работа машины, по условию, полностью определяется ее состоянием qi и содержимым аj, обозреваемой в этот момент времени ячейки, то для каждых qi и аj (i = 1, … , m; j = 1, … , n) программа машины должна содержать единственную команду, начинающуюся символами qi аj. Поэтому программа МТ с внешним алфавитом А и алфавитом внутренних состояний Q содержит не более чем т(п + 1) команду.
Словом в алфавите А, в алфавите Q или в алфавите АÈQ называется последовательность букв соответствующего алфавита.
Под k-конфигурацией будем понимать изображение ленту МТ с информацией, сложившейся на ней к началу k-го шага или слово в алфавите АÈQ, записанное на ленту к началу k-го шага с указанием того, какая ячейка обозревается в этот шаг и в каком состоянии находится машина (00011101q1110 – в состоянии q1 обозревается вторая с правого края непустого слова ячейка с записанным на ней символом 1).
Имеют смысл лишь конечные конфигурации.
Конфигурация называется заключительной, если состояние, в котором при этом находится машина, заключительное (q0).
Если выбрать какую-либо незаключительную конфигурацию МТ в качестве исходной, то работа МТ будет состоять в том, чтобы последовательно преобразовывать исходную конфигурацию в соответствии с программой МТ до тех пор, пока не будет достигнута заключительная конфигурация. После этого работа МТ считается законченной, а результатом работы считается достигнутая заключительная конфигурация.
Говорят, что непустое слово a в алфавите А воспринимается машиной в стандартном положении, если оно записано в последовательных ячейках ленты, все остальные ячейки пусты (в них записаны пустые буквы) и МТ обозревает крайнюю справа ячейку из тех, в которых записано слово a.
Стандартное положение называется начальным (заключительным), если МТ, воспринимающая слово в стандартном положении, находится в начальном состоянии q1 (в заключительном состоянии q0).
Говорят, что слово a перерабатывается машиной в слово b (a→b), если от слова a, воспринимаемого машиной в стандартном начальном положении (СНП), МТ, после выполнения конечного числа команд, приходит к слову b, воспринимаемому в положении остановки.
Применение МТ к словам
Задача 1: Дана МТ с внешним алфавитом А = {0, 1}, Q = {q0, q1} и программой d: q10→q20П; q20→q01; q11→q11П; q21→q21П. В какое слово переработает МТ слово a = 101 из СНП?
Решение. Изобразим работу МТ с помощью ленты:
| … | 0 | 1 | 0 | q1 1 | 0 | … |
1) начальная конфигурация: в состоянии q1 обозревается крайняя правая непустая ячейка, то есть ячейка, в которой записана правая крайняя 1 данного слова. Выполняется команда (3), которая начинается с пары q11. В состоянии q1 вижу символ 1, меняю символ 1 на символ 1, перехожу вправо на одну ячейку, меняю состояние на q1.
| … | 0 | 1 | 0 | 1 | q1 0 | … |
2) вторая конфигурация: в состоянии q1 обозревается символ 0. Выполняется команда (1), которая начинается с пары q10. В состоянии q1 вижу 0, меняю символ 0 на символ 0, двигаюсь вправо на одну ячейку, перехожу в состояние q2.
| … | 0 | 1 | 0 | 1 | 0 | q20 | … |
3) третья конфигурация: в состоянии q2 обозревается символ 0. Выполняется команда (2), которая начинается с пары q20. В состоянии q2 вижу символ 0, меняю 0 на символ 1, остаюсь на месте, меняю состояние на q0.
| … | 0 | 1 | 0 | 1 | 0 | q01 | … |
4) заключительная конфигурация: то есть слово a = 101 переработалось в слово b = 10101.
Полученную последовательность конфигураций можно записать более коротким способом: 10q11→101q10→1010q20→1010q01. В этом способе пустые символы вне слова записываются только тогда, когда в них возникает потребность (когда машина выходит за пределы данного непустого слова). Этот способ записи короче предыдущего, но не удобен для проверки. Гораздо удобнее вариант, когда каждая следующая конфигурация записывается под предыдущей. Например, покажем решение задачи для слова a = 101011:
10101q11 «В состоянии q1 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q1»
101011q10 «В состоянии q1 вижу 0, меняю 0 на 0, двигаюсь вправо, меняю состояние на q2»
1010110q20 «В состоянии q2 вижу 0, меняю 0 на 1, остаюсь на месте, меняю состояние на q0»
1010110q01 – это заключительная конфигурация.
При записи каждой следующей конфигурации поступаем так: сначала записываем новый символ (на который меняется обозреваемый), затем символ, через который перешагиваем (при движении вправо – это тот символ, который мы изменяли), затем новое состояние и затем переписываем все оставшиеся символы (крайние пустые символы при этом можно не писать). При этом надо внимательно следить за тем, чтобы количество тех символов, которые не участвовали в работе на данном шаге, после выполнения шага не изменилось (не потерялись или не появились лишние символы).
Задача 2: МТ задана внешним алфавитом А = {0; 1; *}, Q = {q0, q1, q2, q3} и программой, которая может быть задана в виде таблицы:
| q1 | q2 | q3 | |
| 0 | q10Л | q31П | q10Л |
| 1 | q20Л | q21Л | q31П |
| * | q00 | q2*Л | q3*П |
то есть первая команда q10→q10Л, вторая команда q20→q31П и так далее.
В какие слова МТ переводит слова a1 = 11*11 и a2 = 11*1?
Решение. Запишем последовательность конфигураций при переработке первого слова:
11*1q11 «В состоянии q1 вижу 1, меняю 1 на 0, перехожу влево, меняю состояние на q2»
11* q210 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
11q2*10 «В состоянии q2 вижу *, меняю * на *, двигаюсь влево, меняю состояние на q2»
1q21*10 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
q211*10 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
q2011*10 «В состоянии q2 вижу 0, меняю 0 на 1, двигаюсь вправо, меняю состояние на q3»
1q311*10 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
11q31*10 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
111q3*10 «В состоянии q3 вижу *, меняю * на *, двигаюсь вправо, меняю состояние на q3»
111*q310 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
111*1q30 «В состоянии q3 вижу 0, меняю 0 на 0, двигаюсь влево, меняю состояние на q1»
111*q11 «В состоянии q1 вижу 1, меняю 1 на 0, перехожу влево, меняю состояние на q2»
111q2*0 «В состоянии q2 вижу *, меняю * на *, двигаюсь влево, меняю состояние на q2»
11q21*0 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
1q211*0 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
q2111*0 «В состоянии q2 вижу 1, меняю 1 на 1, двигаюсь влево, меняю состояние на q2»
q20111*0 «В состоянии q2 вижу 0, меняю 0 на 1, двигаюсь вправо, меняю состояние на q3»
1q3111*0 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
11q311*0 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
111q31*0 «В состоянии q3 вижу 1, меняю 1 на 1, двигаюсь вправо, меняю состояние на q3»
1111q3*0 «В состоянии q3 вижу *, меняю * на *, двигаюсь вправо, меняю состояние на q3»
1111*q30 «В состоянии q3 вижу 0, меняю 0 на 0, двигаюсь влево, меняю состояние на q1»
1111q1* «В состоянии q1 вижу *, меняю * на 0, меняю состояние на q0 и останавливаюсь»
1111q00 – заключительная конфигурация.
Таким образом, слово a1 = 11*11 было преобразовано в слово b = 1111.
При переработке слов фразы в кавычках проговариваются, но не записываются. В следующем примере попробуйте по записанной конфигурации произнести требуемую фразу самостоятельно:
11*q11
11q2*0 (так как крайний пустой символ может не записываться, то в следующих конфигурациях писать его не будем)
1q21*
q211*
q2011*
1q311*
11q31*
111q3*
111*q30
111q1*
111q00
Таким образом, слово a2 = 11*1 переработалось в слово b = 111. Можно сделать предположение, что данная МТ выполняет сложение натуральных числе в единичной системе счисления. Убедитесь в этом, выполнив преобразования нескольких других слов.
Конструирование МТ
Сконструировать МТ – значит написать ее программу. В этом процессе 4 этапа:
1) сначала создается алгоритм вычисления значений функции;
2) алгоритм записывается на языке МТ;
3) записанная программа проверяется (в том числе на граничных значениях);
4) если не программа работает не для всех проверенных слов, то осуществляется модификация (доработка) программы.
Задача 3: Построить МТ, которая из п записанных подряд единиц оставляла бы на ленте (п – 2) единицы, также записанные подряд, если п ≥ 2, и работала бы вечно, если п = 0 или п = 1.
Решение. 1 этап. Для решения задачи достаточно, если МТ из СНП, двигаясь влево, сотрет две из записанных единиц и после этого остановится.
2 этап. Начнем решать задачу для п ≥ 2. Зададим внешний алфавит А = {0, 1}, и первоначальный алфавит внутренних состояний Q = {q0, q1}, который в процессе решения задачи может дополняться другими состояниями.
Начальная конфигурация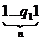 
. Сотрем первую обозреваемую 1 (заменим ее на 0), сдвинемся на одну ячейку влево и перейдем в новое состояние q2. Если мы не перейдем в новое состояние, то машина будет заменять единицы на нули до тех пор, пока единицы не кончатся. Соответствующая команда имеет вид: q11→q21Л
Получим следующую конфигурацию 
. Теперь машина должна стереть вторую единицу и остановиться. Запишем нужную команду: q21→q00. Полученная заключительная конфигурация имеет вид 
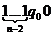и удовлетворяет условию задачи.
Теперь опишем случаи п = 0 и п = 1. Для случая п = 0 в состоянии q1 МТ обозревает ячейку, в которой записан 0. Следовательно, чтобы работать вечно, машина должна двигаться вправо или влево, оставаясь все время в состоянии q1 (так как п = 0, то на ленте записаны только пустые символы). Соответствующая команда имеет вид q10→q10П(Л).
Для случая п = 1 начальная конфигурация имеет вид 0q11. Тогда в состоянии q2 на следующем шаге работы программы машина будет обозревать ячейку, в которой находится 0. Так как теперь на ленте нет ни одного непустого символа (единственную 1 мы стерли на предыдущем шаге), то мы можем поступить одним из следующих способов: 1) перейти к состоянию q1 (как в случае с п = 0) или 2) оставаясь в состоянии q2, двигаться влево или вправо по ленте, ничего не меняя. То есть выбрать одну из следующих команд: q20→q20П; q20→q20Л; q20→q10П; q20→q10Л.
Теперь все составленные команды запишем в программу с помощью таблицы:
| q1 | q2 | |
| 0 | q10П | q10П |
| 1 | q20Л | q00 |
3 этап. Проверяем работу программы. В качестве проверочных слов возьмем: a1 = 11, a2 = 11111, a3 = 1 и a4 = 0.
| Начальная конфигурация | 1q11 | 111q11 | q11 | q10 |
| 1 шаг | q210 | 11q210 | q200 | 0q10 |
| 2 шаг | q000 | 11q000 | 0q10 | 00q10 |
| 3 шаг | … | … |
Таким образом, проверка показала, что при наименьшем числе (п = 2), при произвольно взятом числе (п = 5) и при крайних значениях работа построенной машины удовлетворяет условию задачи. Следовательно, считаем, что задача решена верно (пока не будет доказано обратное).
Вычислимые по Тьюрингу функции
Функция называется вычислимой по Тьюрингу, если существует МТ, ее вычисляющая, то есть такая МТ, которая вычисляет ее значения для тех наборов значений аргументов, для которых функция определена, и работающая вечно, если функция для данного набора значений аргументов не определена.
Для того, чтобы определение стало до конца точным, необходимо выполнение следующих условий:
1) Считают, что речь идет о функциях (или частичных функциях, то есть не всюду определенных), заданных на множестве N и принимающих значения также из N.
2) Необходимо договориться о том, как записывать на ленте МТ значения х1, х2, … , хп аргументов функции f(х1, х2, … , хп), из какого положения начинать переработку исходного слова и в каком положении получать значения функции.
Договоримся поступать следующим образом:
Значения аргументов х1, х2, … , хп будем располагать на ленте в виде следующего слова: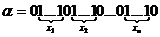 
. Для 
обозначим 
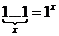и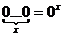 
. Дополнительно полагаем: 
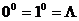– пустое слово. Так что на слова 10 = L, 11 = 1, 12 = 11, 13 = 111, ... будем смотреть как на «изображения» натуральных чисел 0, 1, 2, 3, ... соответственно. Таким образом, предыдущее слово a можно представить следующим образом: 
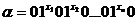. Далее, начинать переработку данного слова будем из стандартного начального положения, т. е. из положения, при котором в состоянии q1, обозревается крайняя правая единица записанного слова. Если функция f(х1, х2, … , хп)определена на данном наборе значений аргументов, то в результате на ленте должно быть записано подряд f(х1, х2, … , хп) единиц; в противном случае машина должна работать бесконечно. При выполнении всех перечисленных условий будем говорить, что машина Тьюринга вычисляет данную функцию. Таким образом, сформулированное в начале пункта определение становится абсолютно строгим.
Обратимся к примерам. Нетрудно понять, что машина Тьюринга из задачи 1 по существу вычисляет функцию f(х) = х + 1, а машина Тьюринга из задачи 3 вычисляет функцию f(х) = х – 2.
Задача 4.Построим машину Тьюринга, вычисляющую функцию f(х) = х/2. Эта функция не всюду определена: областью ее определения является лишь множество всех четных чисел. Поэтому, учитывая определение, нужно сконструировать такую машину Тьюринга, которая при подаче на ее вход четного числа давала бы на выходе половину этого числа, а при подаче нечетного – работала бы неограниченно долго.
Сконструировать машину Тьюринга – значит написать (составить) ее программу. В этом процессе четыре этапа: сначала создается алгоритм вычисления значений функции, затем он записывается на языке машины Тьюринга (программируется); после составления программы происходит ее проверка и, если необходимо – модификация (улучшение) программы.
В качестве внешнего алфавита возьмем двухэлементное множество А = {0, 1}. В этом алфавите натуральное число х изображается словом 11... 1, состоящим из х единиц, которое на ленте машины Тьюринга записывается в виде х единиц, стоящих в ячейках подряд. Работа машины начинается из стандартного начального положения: 01... 1q110 (число единиц равно х).
Сделаем начало вычислительного процесса таким: машина обозревает ячейки, двигаясь справа налево, и каждую вторую единицу превращает в 0. Такое начало обеспечивается следующими командами:
(1): q11→q21Л;
(2): q21→q10Л;
(3): q20→q20Л.
Если число х единиц нечетно, то машина продолжит движение по ленте влево неограниченно, т. е. будет работать бесконечно. Если же число х единиц четно, то в результате выполнения команд создается конфигурация q20010101... 01010, в которой число единиц равно х/2. Остается сдвинуть единицы так, чтобы между ними не стояли нули. Для осуществления этой процедуры предлагается следующий алгоритм. Будем двигаться по ленте вправо, ничего на ней не меняя, до первой единицы и перейдем за единицу. Передвижение осуществляется с помощью следующих команд:
(4): q10→q30П;
(5): q30→q30П;
(6): q31→q41П.
В результате их выполнения получим конфигурацию 001q4010101 ... 010100.(*)
Заменим 0, перед которым остановились, на 1 и продвинемся вправо до ближайшего 0:
(7): q40→q51П;
(8): q51→q51П.
Получим конфигурацию 00111q50101... 010100, в которой правее обозреваемой ячейки записаны «пары» 01, ..., 01. Кроме того, на ленте одна единица записана лишняя. Продвинемся по ленте вправо до последней «пары» 01. Это можно сделать с помощью своеобразного цикла:
(9): q50→q60П;
(10): q61→q51П.
Получим конфигурацию 001110101 ...01010q600. Двигаться дальше вправо бессмысленно. Вернемся на две ячейки назад и заменим единицу из последней «пары» 01 на ноль:
(11): q60→q70Л;
(12): q70→q70Л;
(13): q71→q80Л.
Получим конфигурацию 001110101 ...01q800. Число единиц на ленте снова равно х/2. Продвинемся влево на одну ячейку с помощью команды
(14): q80→q90Л.
В результате чего получим конфигурацию 001110101 ...010 q910. Теперь уничтожим самую правую единицу и продвинемся по ленте влево до следующей единицы:
(15): q91→q100Л;
(16): q100→q100Л. Получим конфигурацию 001110101 ... 0 q10100 (**), в которой левее обозреваемой ячейки записана серия пар 10, 10, ..., 10 (если читать справа налево). Теперь на ленте недостает одной единицы, т. е. число единиц равно (х/2) - 1. Продвинемся по ленте влево до последней «пары» 10. Это можно сделать с помощью цикла
(17): q101→q111Л;
(18): q110→q100Л,
выполнив который, придем к следующей конфигурации: 001q11110101...0100. Вернемся вправо к ближайшему нулю и превратим его в единицу:
(19): q111→q121П;
(20): q121→q121П;
(21): q120→q131П.
Получим конфигурацию 001111q13101 ... 0100, в которой число единиц снова равно х/2.
Если теперь перешагнем вправо по ленте через обозреваемую единицу и переведем машину в состояние q4 помощью команды
(22): q131→q41П
то придем к следующей конфигурации: 0011111q401 ... 0100, которая по существу аналогична конфигурации (*). В результате программа зацикливается (становится циклической): снова ближайший 0 превращается в 1, а самая правая 1 – в 0, затем машина возвращается к самому левому нулю, оказываясь в начале следующего цикла, и т.д.
Как же завершается работа программы? В некоторый момент конфигурация будет иметь вид 00111... 1110q1010. Выполнив команды (17), (18), придем к конфигурации 00111... q11110100. Далее выполняются команды (19), (20), (21), что приводит к конфигурации: 00111... 111111q1300. Остается остановить машину. Это делается с помощью команды
(23): q130→q00Л.
Заключительная конфигурация имеет вид: 00111... 1111q0100. Запишем программу машины Тьюринга в табличной форме:
| q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | q9 | q10 | q11 | q12 | q13 | |
| 0 | q30П | q20Л | q30П | q51П | q60П | q70Л | q70Л | q90Л | q100Л | q100Л | q131П | q00Л | |
| 1 | q21П | q10Л | q41П | q51П | q51П | q80Л | q100Л | q111Л | q121П | q121П | q41П |
Проверим работу машины для слова a1 = 0110.
01q110
0q2110
q10010
0q3010
00q310
001q40
0011q50
00110q60
0011q70
001q710
00q810 и на этом шаге мы обнаруживаем, что ситуация не предусмотрена программой. На ленте записано число, в два раза меньше исходного и на следующем шаге машина должна закончить работу. Дополним программу машины командой q81→q01.
Предлагается самостоятельно проследить за работой этой машины Тьюринга, взяв в качестве исходных конкретные слова: 111, 1111, 111111, 1111111111.
Видим, что дальнейшая проверка показала отсутствие противоречий в работе программы, поэтому окончательно программа машины имеет вид:
| q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | q9 | q10 | q11 | q12 | q13 | |
| 0 | q30П | q20Л | q30П | q51П | q60П | q70Л | q70Л | q90Л | q100Л | q100Л | q131П | q00Л | |
| 1 | q21П | q10Л | q41П | q51П | q51П | q80Л | q01 | q100Л | q111Л | q121П | q121П | q41П |
Тезис Тьюринга (основная гипотеза теории алгоритмов).Вернемся к интуитивному представлению об алгоритмах. Напомним, одно из свойств алгоритма заключается в том, что он представляет собой единый способ, позволяющий для каждой задачи из некоего бесконечного множества задач за конечное число шагов найти ее решение.
На понятие алгоритма можно взглянуть и с несколько иной точки зрения. Каждую задачу из бесконечного множества задач можно выразить (закодировать) некоторым словом некоторого алфавита, а решение задачи – каким-то другим словом того же алфавита. В результате получим функцию, заданную на некотором подмножестве множества всех слов выбранного алфавита и принимающую значения в множестве всех слов того же алфавита. Решить какую-либо задачу – значит найти значение этой функции на слове, кодирующем данную задачу. А иметь алгоритм для решения всех задач данного класса – значит иметь единый способ, позволяющий в конечное число шагов «вычислять» значения построенной функции для любых значений аргумента из ее области определения. Таким образом, алгоритмическая проблема – по существу, проблема о вычислении значений функции, заданной в некотором алфавите. Остается уточнить, что значит уметь вычислять значения функции. Это значит вычислять значения функции с помощью подходящей машины Тьюринга. Для каких же функций возможно их тьюрингово вычисление? Многочисленные исследования ученых, обширный опыт показали, что такой класс функций чрезвычайно широк. Каждая функция, для вычисления значений которой существует какой-нибудь алгоритм, оказывалась вычислимой посредством некоторой машины Тьюринга. Это дало повод Тьюрингу высказать следующую гипотезу, называемую основной гипотезой теории алгоритмов, или тезисом Тьюринга:
Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция является вычислимой по Тьюрингу, т. е. когда она может вычисляться на подходящей машине Тьюринга.
Это означает, что строго математическое понятие вычислимой (по Тьюрингу) функции является по существу идеальной моделью взятого из опыта понятия алгоритма. Данный тезис есть не что иное, как аксиома, постулат, выдвигаемый нами, о взаимосвязях нашего опыта с той математической теорией, которую мы под этот опыт хотим подвести. Конечно же данный тезис в принципе не может быть доказан методами математики, потому что он не имеет внутриматематического характера (одна сторона в тезисе – понятие алгоритма – не является точным математическим понятием). Он выдвинут исходя из опыта, и именно опыт подтверждает его состоятельность. Точно так же, например, не могут быть доказаны и математические законы механики; они открыты Ньютоном и многократно подтверждены опытом.
Впрочем, не исключается принципиальная возможность того, что тезис Тьюринга будет опровергнут. Для этого должна быть указана функция, которая вычислима с помощью какого-нибудь алгоритма, но невычислима ни на какой машине Тьюринга. Но такая возможность представляется маловероятной (в этом одно из значений гипотезы): всякий алгоритм, который будет открыт, может быть реализован на машине Тьюринга.
Машины Тьюринга и современные электронно-вычислительные машины.Изучение машин Тьюринга и практика составления программ для них закладывают фундамент алгоритмического мышления, сущность которого состоит в том, что нужно уметь разделять тот или иной процесс вычисления или какой-либо другой деятельности на простые составляющие шаги. В машине Тьюринга расчленение (анализ) вычислительного процесса на простейшие операции доведено до предельной возможности: распознавание единичного рассмотренного вхождения символа, перемещение точки наблюдения данного ряда символов в соседнюю точку и изменение имеющейся в памяти информации. Конечно, такое мелкое дробление вычислительного процесса, реализуемого в машине Тьюринга, значительно его удлиняет. Но вместе с тем логическая структура процесса, расчлененного, образно выражаясь, до атомарного состояния, значительно упрощается и предстает в некотором стандартном виде, весьма удобном для теоретических исследований. (Именно такое расчленение на простейшие составляющие вычислительного процесса на машине Тьюринга дает еще один косвенный аргумент в пользу тезиса Тьюринга, обсуждавшегося в предыдущем пункте: всякая функция, вычисляемая с помощью какого-либо алгоритма, может быть вычислена на машине Тьюринга, потому что каждый шаг данного алгоритма можно расчленить на еще более мелкие операции, которые реализуются в машине Тьюринга.) Таким образом, понятие машины Тьюринга есть теоретический инструмент анализа алгоритмического процесса, а значит, анализа существа алгоритмического мышления.
В современных ЭВМ алгоритмический процесс расчленен не на столь мелкие составляющие, как в машинах Тьюринга. Наоборот, создатели ЭВМ стремятся к известному укрупнению выполняемых машиной процедур (на этом пути, конечно, есть свои ограничения). Так, для выполнения операции сложения на машине Тьюринга составляется целая программа, а в современной ЭВМ такая операция является простейшей.
Далее, машина Тьюринга обладает бесконечной внешней памятью (неограниченная в обе стороны лента, разбитая на ячейки). Но ни в одной реально существующей машине бесконечной памяти быть не может. Это говорит о том, что машины Тьюринга отображают потенциальную возможность неограниченного увеличения объема памяти современных ЭВМ.
Наконец, можно провести более подробный сравнительный анализ работы современной ЭВМ и машины Тьюринга. В большинстве ЭВМ принята трехадресная система команд, обусловленная необходимостью выполнения бинарных операций, в которых участвует содержимое сразу трех ячеек памяти. Например, число из ячейки а умножается на число из ячейки b, и результат отправляется в ячейку с. Существуют ЭВМ двухадресные и одноадресные. Так, одноадресная ЭВМ работает следующим образом: вызывается (в сумматор) число из ячейки а; в сумматоре происходит, например, умножение этого числа на число из ячейки b, результат отправляется из сумматора в ячейку с. Машину Тьюринга можно считать одноадресной машиной, в которой система одноадресных команд упрощена еще больше: на каждом шаге работы машины команда предписывает замену лишь единственного знака, хранящегося в обозреваемой ячейке, а адрес обозреваемой ячейки при переходе к следующему такту может меняться лишь на единицу (обозрение соседней справа или слева ячейки ленты) или не меняться вовсе. Это удлиняет процесс, но в то же время резко унифицирует его, делает стандартным.
Подводя итоги, можно сказать, что современные ЭВМ есть некие реальные физические модели машин Тьюринга, огрубленные с точки зрения теории, но созданные в целях реализации конкретных вычислительных процессов. В свою очередь, понятие машины Тьюринга и теория таких машин есть теоретический фундамент и обоснование современных ЭВМ.
Нормальные алгоритмы Маркова
Теория нормальных алгоритмов (или алгорифмов, как называл их создатель теории) была разработана советским математиком А.А. Марковым (1903-1979) в конце 1940-х – начале 1950-х гг XX в. Эти алгоритмы представляют собой некоторые правила по переработке слов в каком-либо алфавите, так что исходные данные и искомые результаты для алгоритмов являются словами в некотором алфавите.
Марковские подстановки.Алфавитом (как и прежде) называется любое непустое множество. Его элементы называются буквами, а любые последовательности букв – словами в данном алфавите. Для удобства рассуждений допускаются пустые слова (они не имеют в своем составе ни одной буквы). Пустое слово будем обозначать L. Если А и В – два алфавита, причем А Ì В, то алфавит В называется расширением алфавита А.
Слова будем обозначать латинскими буквами: Р, Q, R (или этими же буквами с индексами). Одно слово может быть составной частью другого слова. Тогда первое называется подсловом второго или вхождением во второе. Например, если А – алфавит русских букв, то можем рассмотреть такие слова: Р1 = параграф, Р2 = граф, Р3 = ра. Слово Р2 является подсловом слова Р1, а Р3 — подсловом Р1 и Р2, причем в Р1 оно входит дважды. Особый интерес представляет первое вхождение.
Определение. Марковской подстановкой называется операция над словами, задаваемая с помощью упорядоченной пары слов (Р, Q), состоящая в следующем. В заданном слове R находят первое вхождение слова Р (если таковое имеется) и, не изменяя остальных частей слова R, заменяют в нем это вхождение словом Q. Полученное слово называется результатом применения марковской подстановки (Р, Q) к слову R. Если же первого вхождения Р в слово R нет (и, следовательно, вообще нет ни одного вхождения Р в R, то считается, что марковская подстановка (Р, Q) неприменима к слову R.
Частными случаями марковских подстановок являются подстановки с пустыми словами: (L,Q), (Р, L), (L,L).
Пример 1. Примеры марковских подстановок рассмотрены в таблице, в каждой строке которой сначала дается преобразуемое слово, затем применяемая к нему марковская подстановка и, наконец, получающееся в результате слово:
| Преобразуемое слово | Марковская подстановка | Результат |
| 138578926 | (85789,00) | 130026 |
| Тарарам | (ара, L) | трам |
| Шрам | (ра, ар) | шарм |
| Функция | (L, С-) | С-функция |
| Логика | (ика, L) | лог |
| Книга | (L, L) | книга |
| Поляна | (пор, т) | [неприменима] |
Для обозначения марковской подстановки (Р, Q) используется запись Р→Q. Она называется формулой подстановки (Р, Q). Некоторые подстановки (Р, Q) будем называть заключительными (смысл названия станет ясен чуть позже). Для обозначения таких подстановок будем использовать запись Р→.Q, называя ее формулой заключительной подстановки. Слово Р называется левой частью, а Q – правой частью в формуле подстановки.
Нормальные алгоритмы и их применение к словам.Упорядоченный конечный список формул подстановок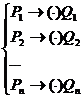 
в алфавите А называется схемой (или записью) нормального алгоритма в А. (Запись точки в скобках означает, что она может стоять в этом месте, а может отсутствовать.) Данная схема определяет (детерминирует) алгоритм преобразования слов, называемый нормальным алгоритмом Маркова. Дадим его точное определение.
Определение. Нормальным алгоритмом (Маркова) в алфавите А называется следующее правило построения последовательности Vi слов в алфавите А, исходя из данного слова V в этом алфавите. В качестве начального слова V0 последовательности берется слово V. Пусть для некоторого i ³ 0 слово Vi построено и процесс построения рассматриваемой последовательности еще не завершился. Если при этом в схеме нормального алгоритма нет формул, левые части которых входили бы в Vi, то Vi+1 полагают равным Vi и процесс построения последовательности считается завершившимся. Если же в схеме имеются формулы с левыми частями, входящими в Vi то в качестве Vi+1 берется результат марковской подстановки правой части первой из таких формул вместо первого вхождения ее левой части в слово Vi; процесс построения последовательности считается завершившимся, если на данном шаге была применена формула заключительной подстановки, и продолжающимся – в противном случае. Если процесс построения упомянутой последовательности обрывается, то говорят, что рассматриваемый нормальный алгоритм применим к слову V. Последний член последовательности называется результатом применения нормального алгоритма к слову V. Говорят, что нормальный алгоритм перерабатывает V в W.
Последовательность Vi будем записывать следующим образом:
.
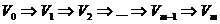Мы определили понятие нормального алгоритма в алфавите А. Если же алгоритм задан в некотором расширении алфавита А, то говорят, что он есть нормальный алгоритм над А.
Рассмотрим примеры нормальных алгоритмов.
Пример 2. Пусть А = {а, b} – алфавит. Рассмотрим следующую схему нормального алгоритма в А.
.
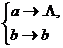Нетрудно понять, как работает определяемый этой схемой нормальный алгоритм. Всякое слово V в алфавите А, содержащее хотя бы одно вхождение буквы а, он перерабатывает в слово, получающееся из V вычеркиванием в нем самого левого (первого) вхождения буквы а. Пустое слово он перерабатывает в пустое. (Алгоритм не применим к таким словам, которые содержат только букву b) Например, ааbаb => аbаb, аb => b, аа => а, bbаb => bbb, bаbа => bbа.
Пример 3. Пусть А = {а0, а1, ..., ап} — алфавит. Рассмотрим схему:
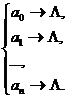
Она определяет нормальный алгоритм, перерабатывающий всякое слово (в алфавите А) в пустое слово. Например, а1а2а1а3а0 => а1а2а1а3 => а2а1а3 => а2а3 => а3 => L; а0а2а2а1а3а1 => а2а2а1а3а1 => а2а2а3а1 => а2а2а3 => а2а3 => а3 => L.
Пример 4. А = {1, 0}. Введем дополнительный алфавит В = {с, +; *}. Рассмотрим схему (для удобства работы запишем команды схемы в столбик):
(1) 00+®0+0
(2) 01+®1+0
(3) 10+®0+1
(4) 11+®1+1
(5) с0®0+0с
(6) с1®1+1с
(7) +®*
(8) *®L
(9) с®.L
(10) L®с
Этот алгоритм любое слово Р в алфавите А переводит в слово РР. Рассмотрим подробно его работу для слова 101.
101 – начальная конфигурация. Поскольку все команды схемы, кроме (10) содержат символы, которых нет в данном слове, то первой выполняем команду (10):
с101 теперь в слове нет подслов, содержащих «+», но есть подслово «с1», значит, выполняем команду (6):
1+1с01 – нет подслов «00+», «01+», «10+», «11+», есть подслово «с0», выполняем команду (5):
1+10+0с1 – нет подслов «00+», «01+», есть подслово «10+»; выполняем команду (3):
1+0+10с1 – теперь снова нет подслов «00+», «01+», «10+», «11+», есть подслово «с1»; выполняем команду (6):
1+0+101+1с – есть подслово «01+»; выполняем команду (2):
1+0+11+01с – есть подслово «11+»; выполняем команду (4):
1+0+1+101с – снова неприменимы команды с (1) по (6), следующая команда – (7). Применяем ее последовательно 3 раза:
1*0*1*101c – теперь неприменимы команды с (1) по (7); следующая по порядку команда – (8). Применяя ее последовательно, получим:
101101с – и, наконец, применяем (9) команду и получаем заключительную конфигурацию:
101101.
Предлагаем самостоятельно переработать слово 1001 и получить слово 10011001.
Нормально вычислимые функции и принцип нормализации Маркова.Как и машины Тьюринга, нормальные алгоритмы не производят собственно вычислений: они лишь производят преобразования слов, заменяя в них одни буквы другими по предписанным им правилам. В свою очередь, мы предписываем им такие правила, результаты применения которых мы можем интерпретировать как вычисления. Рассмотрим два примера.
Пример 5. В алфавите А = {1} схема L®.1 определяет нормальный алгоритм, который к каждому слову в алфавите А = {1} (все такие слова суть следующие: L, 1, 11, 111, 1111, 11111 и т. д.) приписывает слева 1. Следовательно, алгоритм реализует (вычисляет) функцию f(х) = х + 1.
Пример 6. Дана функция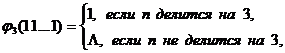 
, где п – число единиц в слове 11...1. Рассмотрим нормальный алгоритм в алфавите А = {1} со следующей схемой:
(1) 111®L
(2) 11®.L
(3) 1®.L
(4) L®.1
Этот алгоритм работает по такому принципу: пока число букв 1 в слове не меньше 3, алгоритм последовательно стирает по три буквы. Если число букв меньше 3, но больше 0, то оставшиеся буквы 1 или 11 стираются заключительно; если слово пусто, оно заключительно переводится в слово 1. Например:
1111111 => 1111 => 1 => L; 111111111 => 111111 => 111 => L => 1.
Таким образом, рассмотренный алгоритм реализует (или вычисляет) данную функцию.
Сформулируем теперь точное определение такой вычислимости функций.
Определение. Функция f, заданная на некотором множестве слов алфавита А, называется нормально вычислимой, если найдется такое расширение В данного алфавита (А Í В) и такой нормальный алгоритм в В, что каждое слово V (в алфавите А) из области определения функции f этот алгоритм перерабатывает в слово f(V).
Таким образом, нормальные алгоритмы примеров 5 и 6 показывают, что функции f (х) = х + 1 и f3(х) нормально вычислимы. Причем соответствующие нормальные алгоритмы удалось построить в том же самом алфавите А, на словах которого были заданы рассматривавшиеся функции, т. е. расширять алфавит не потребовалось (В = А). Следующий пример демонстрирует нормальный алгоритм в расширенном алфавите, вычисляющий данную функцию.
Пример 7. Построим нормальный алгоритм для вычисления функции f(х) = х + 1 не в одноичной системе (как сделано в примере 5), а в десятичной. В качестве алфавита возьмем перечень арабских цифр А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, а нормальный алгоритм будем строить в его расширении В = А È {а, b}. Вот схема этого нормального алгоритма (читается по столбцам):
0b®.1 а0®0а 0а®0b
1b®.2 а1®1а 1а®1b
2b®.3 а2®2а 2а®2b
3b®.4 а3®3а 3а®3b
4b®.5 а4®4а 4а®4b
5b®.6 а5®5а 5а®5b
6b®.7 а6®6а 6а®6b
7b®.8 а7®7а 7а®7b
8b®.9 а8®8а 8а®8b
9b®b0 а9®9а 9а®9b
b®.1 L®а
Попытаемся применить алгоритм к пустому слову L. Нетрудно понять, что на каждом шаге должна будет применяться самая последняя формула данной схемы. Получается бесконечный процесс:
L => а => аа => ааа => аааа =>...
Это означает, что к пустому слову данный алгоритм не применим.
Если применить теперь алгоритм к слову 499, получим следующую последовательность слов: 499 => а499 (применена последняя формула) => 4а99 (формула из середины второго столбца) => 49а9 => 499а (дважды применена формула из конца второго столбца) => 499b (предпоследняя формула) => 49b0 => 4b00 (дважды применена предпоследняя формула первого столбца) => 500 (применена формула из середины первого столбца).
Таким образом, слово 499 перерабатывается данным нормальным алгоритмом в слово 500. Предлагается проверить, что 328 => 329, 789 => 790.
В рассмотренном примере нормальный алгоритм построен в алфавите В, являющемся существенным расширением алфавита А (т.е. А Ì В и А ¹ В), но данный алгоритм слова в алфавите А перерабатывает снова в слова в алфавите А. В таком случае говорят, что алгоритм задан над алфавитом А. Создатель теории нормальных алгоритмов советский математик А.А.Марков выдвинул гипотезу, получившую название «Принцип нормализации Маркова». Согласно этому принципу, для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально вычислима.
Сформулированный принцип, как и тезис Тьюринга, носит внематематический характер и не может быть строго доказан. Он выдвинут на основании математического и практического опыта.
Все, что ранее было сказано о тезисе Тьюринга, можно с полным правом отнести к принципу нормализации Маркова.
Дата добавления: 2018-02-28; просмотров: 13133; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!