Основные свойства определенного интеграла
Свойство 1. Если 
и функция 
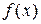интегрируема на отрезке 
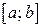, то
.
Свойство 2. Если функции 
и 
интегрируемы на отрезке 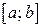, тогда интегрируема на 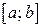их сумма. Интеграл суммы равен сумме интегралов.
.
Доказательство.
.
Свойство 3. 
.
Свойство 4 (свойство аддитивности). Если функция 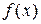интегрируема на отрезке 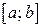и 
, то интеграл по всему отрезку равен сумме интегралов по частям этого отрезка:
,
Свойство 5 (теорема о среднем). Если функция 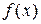непрерывна на отрезке 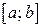, то существует точка 
, такая, что справедливо равенство
. (1)
Доказательство. Пусть 
. Согласно теореме об ограниченности непрерывной на отрезке 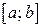функции имеем 
, где 
- наименьшее значение функции, а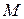 
- наибольшее значение функции на отрезке .
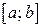Очевидно, что если взять произвольное разбиение отрезка 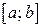, то справедливы неравенства
.
Перейдем к пределу в неравенствах, если 
. Тогда получаем 
.
Далее 
,
Откуда 
.
Непрерывная на отрезке функция принимает на нем все свои промежуточные значения между и 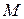. Поэтому найдется точка , такая, что 
,откуда следует формула (1).
Если 
, то 
.
,
Свойство 5 (теорема о среднем) при 
имеет простой геометрический смысл: значение определенного интеграла, при некотором , равно площади прямоугольника с высотой 
и основанием 
. Число
Дата добавления: 2015-12-18; просмотров: 13; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!