Глава 2. Двойственность в банаховых пространствах

Пространства и тесно взаимосвязаны. Ряд этих связей будет выявлен в этой главе. Элементы сопряженного пространства будем обозна-чать , а значение через .

Изометрические вложения. Рефлексивность

Следующий результат устанавливает некоторые свойства двойственности.

Т е о р е м а 1. Пусть линейное нормированное пространство и замкнутый единичный шар в нем. Пусть также замкнутый единичный шар в . Тогда

(i)

(ii) .

Д о к а з а т е л ь с т в о. (i) следует из определения операторной нормы.

Для доказательства (ii) фиксируем . Отображение определяет линейный функционал на . Кроме того,

Следовательно, определяет линейный непрерывный функционал и . С другой стороны, по одному из следствий теоремы Хана – Банаха найдется такой ,что и . Но тогда для будем иметь

Отсюда и, следовательно, .

Из теоремы 1 следует, что каждый порождает элемент из . При этом отображение является изометрическим вложе-нием.

О п р е д е л е н и е. Если изометрическое вложение сюръек-тивно, то называется рефлексивным пространством.

Т е о р е м а 2. Если нормированные пространства и , то

Д о к а з а т е л ь с т в о. Действительно, из теоремы 1 и определения нормы оператора получается

Слабые сходимости (топологии)

Слабая сходимость элементов. Пусть нормированное пространство. Для произвольных и конечного множества определим

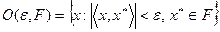. (1)

Очевидно, что является открытым множеством, содержащим нуль. Пересечение конечного числа множеств вида (1) содержит множество такого вида, поскольку

Следовательно, совокупность множеств вида (1) можно взять в качестве определяющей системы окрестностей нуля некоторой топологии. Полученная топология будет слабее исходной. Из теоремы о достаточном числе функционалов следует, что она удовлетворяет аксиоме отделимости Хаусдорфа. Однако слабая топология может не удовлетворять первой аксиоме счетности и потому быть неметризуемой. Тем не менее сходимость в , определяемая этой топологией, представляет собой важное понятие.

О п р е д е л е н и е. Последовательность элементов нормирован-ного пространства называется слабо сходящейся к элементу , если выполняется соотношение

Наличие аксиомы отделимости Хаусдорфа влечет единственность предела слабо сходящейся последовательности. Для обозначения слабой сходимости будем использовать запись

Т е о р е м а 1. Всякая слабо сходящаяся последовательность ограниче-на.

Д о к а з а т е л ь с т в о. Пусть . Рассмотрим в последователь-ность , соответствующую последовательности при изометрическом вложении в . По условию при . Другими словами, для последовательности выполнены условия теоремы Банаха – Штейнгауса, в силу которой

Слабая сходимость функционалов. Пространство можно рассматривать двояко: либо как основное пространство, связывая с ним , либо как пространство линейных ограниченных функционалов на . Поэтому наряду с сходимостью возникает еще один вид слабой сходимости.

О п р е д е л е н и е. Последовательность называется сла-бо сходящейся к , если выполняется условие

при .

З а м е ч а н и е. В пространстве слабая топология слабее, чем слабая топология. Они совпадают в случае, когда рефлексивно. Из теоремы Банаха – Штейнгауса следует также ограниченность слабо сходящейся последовательности, если банахово пространство.

Значение слабой сходимости видно из следующего результата.

Т е о р е м а 2 (Б а н а х а – А л а о г л у). Пусть сепарабельное нормированное пространство. Тогда из всякой ограниченной последователь-ности можно выделить слабо сходящуюся подпоследователь-ность.

Д о к а з а т е л ь с т в о. По условию . Пусть счет-ное всюду плотное в подмножество. Используя диагональный метод Кан-тора, выбираем подпоследовательность , сходящуюся на всех элементах . Покажем, что последовательность сходится и при лю-бом . Действительно, для фиксированных и выберем 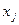так, чтобы выполнялось условие . Но тогда

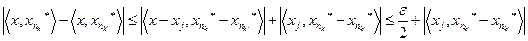Однако второе слагаемое можно сделать меньше при больше неко-торого номера. Таким образом, числовая последовательность фунда-ментальна, а потому сходится. Определим теперь на функционал

Очевидно, что линейный функционал. Кроме того,

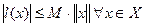Следовательно, и теорема доказана.

Описание сопряженных пространств

Пространство, сопряженное к пространству Лебега.

Т е о р е м а 1. Пусть , , пространство с конечной мерой. Пространство изометрически изоморфно прост-ранству . Соответствующий изоморфизм задается формулой

. (2)

Д о к а з а т е л ь с т в о. Пусть . Тогда формула (2) определяет ли-нейный функционал на и в силу неравенства Гельдера имеем

Отсюда видно, что функционал ограничен и . Таким образом, уста-новлено включение .

Остается доказать, что любой функционал 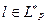можно представить в виде (2) с некоторой функцией и .

Пусть 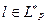. Для имеем 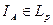и поэтому определено отобра-жение или по формуле . Если причем пере-сечение и пусто при , то и ряд сходится в пространстве . Поэтому линейность и непрерывность влечет

Тем самым доказана счетная аддитивность . Последнее означает, что

заряд (комплекснозначный). Более того, является абсолютно непрерывным относительно меры 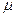. Действительно, если , то 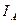почти всюду равна нулю, т.е. является нулем в и . Поэтому в силу теоремы Радона – Никодима существует такая функция , что

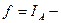Покажем теперь, что и что выполняется (2) для каждой . В случае когда индикатор, представление (2) проверяется непосредственно

В силу линейности функционала и интеграла Лебега представление (2) распространяется и на простые функции. Для ограниченной измеримой функции можно построить последовательность простых измеримых функ-ций , сходящихся равномерно к . В силу теоремы Лебега и непрерыв-ности функционала предельный переход в равенстве

дает представление (2) и в этом случае.

Рассмотрим для каждого натурального функции

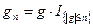, , где

Эти функции ограничены, измеримы и

Записывая теперь неравенство 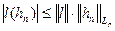с учетом полученных соотноше-ний, получим

Поскольку при всех , то применение теоремы Фату дает

Таким образом, совпадает на множестве ограниченных функций с функцио-налом, задаваемым формулой (2). Поскольку множество ограниченных функ-ций плотно в , то это совпадение распространяется на все пространство и теорема доказана.

Пространство, сопряженное к гильбертову пространству.

Т е о р е м а 2. Пусть гильбертово пространство. Тогда существует единственный элемент такой, что

При этом . Обратно, данная формула определяет функционал

с нормой .

Доказательство теоремы приведено в [1, стр. 202 - 203].

Сопряженный оператор

Пусть линейные нормированные пространства и ли-нейный ограниченный оператор. Для каждого композиция будет представлять линейный непрерывный функционал на , т.е. . Таким образом, определено отображение , действующее по формуле

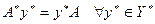Это отображение называют сопряженным оператором к оператору . Его определение особенно естественно выглядит в терминах двойственности:

Следующий результат показывает, что отображение 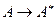является изометрическим изоморфизмом пространств и .

Т е о р е м а 1. Пусть линейные нормированные пространства и линейный ограниченный оператор, действующий из в 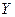. Тогда линейный ограниченный оператор, действующий из в , и

Д о к а з а т е л ь с т в о. Покажем вначале линейность оператора . Пусть произвольные элементы из . Тогда будем иметь

т.е. .

Аналогично, если и , то

т.е. . Линейность доказана.

Наконец, используя соотношения двойственности, получим

Таким образом, 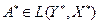и .

Т е о р е м а 2. Пусть банаховы пространства.Оператор

компактен тогда и только тогда, когда, когда компактен оператор .

Д о к а з а т е л ь с т в о. Допустим вначале, что . Нам нужно показать, что единичный шар пространства переводится посредством в предкомпактное множество. Пусть 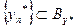. Определим на последовательность функций

Множество является предкомпактным и для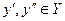

т.е. семейство равностепенно непрерывно. Оно также равномерно ограничено

По теореме Арцела из него можно выделить равномерно сходящуюся на подпоследовательность . Замечая теперь, что

приходим к фундаментальности последовательности . Поскольку банахово пространство, то эта последовательность сходится и компакт-ность оператора доказана.

Обратное утверждение можно вывести аналогичными рассуждениями. Однако, можно воспользоваться уже доказанным.

Пусть 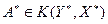. По доказанному является компакт-ным оператором. Пусть изометрические вложения. Тогда . Действительно, имеем

Поскольку 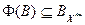, то относительно компактное мно-жество. В силу изометричности таковым является и множество , что и доказывает компактность .

В случае, когда операторы действуют в одном и том же пространстве , т.е. , образует алгебру. Следующий результат касается свойств отображения 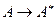в алгебре .

Т е о р е м а 3. Пусть линейное нормированное пространство над полем и . Тогда

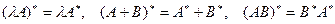Д о к а з а т е л ь с т в о. Проверим последнее соотношение. Пусть и - произвольны. Тогда

откуда следует, что . Остальные соотношения проверяются анало-гично.

Литература

1. Колмогоров, А.Н. Элементы теории функций и функционального анализа. [Текст]/ А.Н. Колмогоров, С.В.Фомин. – М.: Физматлит, 2004.

Дата добавления: 2015-12-17; просмотров: 26; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!