Тема 3. Основы комбинаторики
В математике существует много задач, в которых требуется из имеющихся элементов составить различные комбинации, вычислять количество комбинаций, образованных по определенному правилу. Такие задачи называются комбинаторными, а раздел математики – комбинаторикой. Комбинаторные задачи решали еще в Древнем Китае и в Римской Империи.
Как раздел математики комбинаторика возникла в XVI веке. Ее развитие связано с именами таких ученых, как Н.Тарталья (1500 – 1557), Б.Паскаль (1623 – 1662), П.Ферма (1601 – 1665), Я.Бернулли (1654 – 1705) и Л.Эйлер (1707 – 1783). Возрождение интереса к комбинаторике относится к 50-м годам XX века. Оно связано с развитием кибернетики и дискретной математики.
Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.
Решение большинства комбинаторных задач основано на применении двух основных правил – правила суммы и правила произведения.
Правило суммы: Если элемент А можно выбрать 
способами, а элемент В - 
способами (причем, ни один из способов выбора элемента А не совпадает со способом выбора элемента В), то выбрать А или В можно 
способами.
Например:
Правило произведения: Если элемент А можно выбрать способами и после каждого такого выбора элемент В можно выбрать , то выбрать упорядоченную пару (А,В) можно 
способами.
Например:
Правила произведения и суммы часто используются в решении задач. Кроме них часто используются следующие специальные формулы:
Перестановки: Перестановками называются различные комбинации, образованные из элементов, расположенных в определенном порядке. Количество перестановок обозначается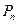 
и вычисляется по формуле: 
, где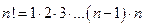 
- произведение всех натуральных чисел от 1 до включительно.
Например:
Размещения: Размещениями называются упорядоченные комбинации, составленные из элементов, отобранных из множества, содержащего элементов (то есть, они могут отличаться друг от друга или составом элементов, или их порядком, или и тем, и другим одновременно). Количество размещений обозначается 
и вычисляется по формуле: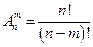 
.
Например:
Сочетания: Сочетаниями называются неупорядоченные комбинации, составленные из элементов, отобранных из множества, содержащего элементов (то есть, они отличаются друг от друга только составом элементов). Количество сочетаний обозначается 
и вычисляется по формуле: 
.
Например:
Дата добавления: 2015-12-17; просмотров: 21; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!