Метод LU-разложения
LU-разложение – это представление матрицы в виде двух: нижней треугольной (L-матрица) и верхней треугольной (U-матрица).
(4)
Условия существования такого разложения даются следующей теоремой.
Если все главные миноры квадратной матрицы А отличны от нуля, то данную матрицу можно разложить на нижнюю треугольную и верхнюю треугольную матрицы, причем это разложение единственное. Заметим также, что U матрица на своей главной диагонали имеет одни единицы.
Формулы, по которым рассчитываются элементы этих матриц, представлены ниже.
(5)
(6)
где n – порядок исходной матрицы;
lij – элемент матрицы L;
uij – элемент матрицы U.
Тогда определитель исходной матрицы равен произведению определителей матриц L и U. Напомним, что определитель треугольной матрицы равен произведению всех элементов, лежащих на главной диагонали. Так как определитель U матрицы всегда равен единице, то достаточно найти определитель матрицы L. В этом и заключается этот метод.
Выделим основной алгоритм.
1 Следует поэлементно перебирать исходную матрицу и запоминать индексы элемента. Если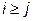 
, то заполнить эту же позицию матрицы L по формуле (5), в противном случае заполнить нулем.
2 Если 
, то заполнить эту же позицию матрицы U по формуле (6), в противном случае заполнить нулем, или, если это элемент главной диагонали, единицей.
3 Продолжать пункты 1 и 2 пока не закончатся элементы исходной матрицы.
|
|
|
4 Найти определитель матрицы L, перемножив ее диагональные элементы.
Так как результат всегда предсказуем, то данный алгоритм легко запрограммировать. Программная реализация алгоритма в среде Mathcad состоит из одного модуля user_lu_expansion(A). Данный модуль возвращает вектор из матриц L и U. Перемножение элементов главной диагонали матрицы L производится в данной реализации условно «вручную».
Осталось проверить исходные матрицы на разложимость. Напомним, что минор матрицы А – это определитель квадратной матрицы порядка n, элементы которого стоят в матрице А на пересечении одинакового числа строк и столбцов, начиная с первой строки и первого столбца. Главным минором называется всякий выделенный минор, у которого номера отмеченных строк совпадают с номерами отмеченных столбцов.
Так очевидно, что в матрицах (1) и (2) не существует нулевых главных миноров. В матрице же (3) видно, что первый главный минор второго порядка нулевой, т.е. матрица в таком виде неразложима. Дальнейший анализ показывает, что главные миноры более высоких порядков ненулевые.
В таких случаях матрицу нужно преобразовать так, чтобы не затронуть значение определителя и исключить существование нулевых главных миноров. Если это невозможно или трудоемко, то лучше отказаться от данного метода.
|
|
|
Но в нашем случае нужно исключить только один нулевой минор второго порядка. Напомним, что на значение определителя не влияет операция сложения строк и операция вычитания одной строки из другой. Так этот минор исключается, например, вычитанием из второй строки третей.
(7)
Проанализировав эквивалентную матрицу, убеждаемся, что нулевых главных миноров больше нет, и матрица становится разложимой. Далее мы будем находить определитель эквивалентной матрицы.
Результаты данного метода следует смотреть в следующей главе.
Метод Гаусса
Вообще методом Гаусса называется метод решения системы линейных алгебраических уравнений, которая приводится в этом методе к ступенчатому виду. Поэтому далее под методом Гаусса мы будем понимать приведение матрицы к ступенчатому виду (к верхней треугольной матрице).
Пусть из исходной матрицы получена верхняя треугольная. Нам известно, что определитель треугольной матрицы находится перемножением элементов, лежащих на главной диагонали. Однако эта матрица не является эквивалентом исходной, поэтому их определители не равны. Чтобы получить определитель исходной матрицы, нужно определитель полученной треугольной матрицы поделить на некоторое число, которое бы компенсировало все операции по приведению исходной матрицы к треугольной. Это число мы будем называть коэффициентом K.
|
|
|
Таким образом, представим формулы, по которым вычисляется определитель.
(8)
(9)
(10)
где B – верхняя треугольная матрица, полученная из исходной;
k – коэффициент строки, получаемый делением диагонального элемента текущего столбца на первый элемент строки, стоящий под диагональным.
Коэффициент K равен произведению всех строковых коэффициентов. Заметим, что строковый коэффициент считается для каждой конкретной строки при текущем столбце один раз.
Выделим основной алгоритм.
Обрабатывать матрицу следует по столбцам, начиная с первого и заканчивая n-1.
1 Найти коэффициент первой строки стоящей под диагональным элементом. Затем каждый элемент этой строки, начиная с первого, умножить на ее коэффициент и из результата вычесть элемент, стоящий в том же столбце, в строке диагонального элемента. В итоге первый элемент обнулится, а последующие заполнятся какими-то числами.
2 Повторять пункт 1 пока не кончатся строки текущего столбца.
|
|
|
3 Перейти на следующий столбец и повторить действия 1 – 2.
4 Продолжать действия 1 – 3 до n-1 столбца включительно.
5 Найти определитель по формуле (9).
Опять же этот алгоритм легко программируется. Программная реализация в среде Mathcad состоит из одного модуля user_Gause(A). Данный модуль возвращает вектор, первый элемент которого коэффициент K, второй – треугольная матрица и третий – значение определителя матрицы А.
Однако, в процессе отладки этого модуля было обнаружено неочевидное с первого взгляда ограничение данного метода, а именно: треугольная матрица должна быть такой, чтобы на ее главной диагонали не получались нули в моменты ее приведения. Иначе происходит обнуление коэффициента K и возникает ошибка деления на ноль. Такая ошибка как раз произошла с матрицей (3). На рисунке 1 показан перехват обнуления коэффициента K в момент работы модуля (листинг модуля смотрите в следующей главе).
Рисунок 1 Аварийная работа модуля
В процессе расчета определителей матриц (1) и (2) такой ошибки не происходит. К сожалению, от данной ошибки нельзя быть застрахованным.
Одним из способов разрешения данной проблемы это найти эквивалент исходной матрицы, сведение которого к треугольному виду не вызывает данную ошибку.
Так был попробован эквивалент, полученный в методе LU-разложения для матрицы (3). В результате модуль успешно завершил расчет.
Результат работы модуля следует смотреть в следующей главе.
Дата добавления: 2015-12-17; просмотров: 32; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!