Задачи, приводящие к дифференциальным уравнениям
При решении многих задач математики, физики и техники часто не удается сразу установить функциональную зависимость между искомыми и данными переменными величинами, но зато удается составить уравнение, связывающее независимую переменную, искомую функцию и ее производную. Такое уравнение называется дифференциальным. Дифференциальное уравнение может не содержать в явном виде независимую переменную и искомую функцию, но обязательно должно содержать одну или несколько производных искомой функции. Например, уравнения y+2y=0, y"+ycosx=lnx являются дифференциальными.
Задача. Найти уравнение кривой, проходящей через точку 
и обладающей следующим свойством: площадь трапеции OAMB, ограниченной осями координат, касательной, проведенной в любой точке M(x,y) искомой кривой, и прямой, проходящей через точку M параллельно оси OY, равна 3.
Решение. Пусть M(x,y) – произвольная точка искомой кривой, уравнение кривой y=f(x). Площадь трапеции OAMB выражается формулой S= 
·. (OA+BM)·OB. Для того, чтобы составить дифференциальное уравнение, выразим отрезки OA, BM, OB через координаты текущей точки (x,y) и через производную y. Из рисунка замечаем BM=y и OA+BM-CM=BM-AC·tgOA+BM-CM. Подставляя эти выражения в формулу для площади трапеции, найдем 
или 
. Это уравнение является дифференциальным уравнением.
Свойства решений (ЛОДУ)
Рассмотрим линейное дифференциальное уравнение n –го порядка
+ 
(x 
+... + 
(x)y' + 
(x)y = f(x).
|
|
|
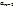с непрерывными коэффициентами (x), 
(x),..., (x), 
(x) и непрерывной правой частью f(x).
Принцип суперпозиции основан на следующих свойствах решений линейных дифференциальных уравнений.
1. Если y1(x) и y2(x)— два решения линейного однородного дифференциального уравнения
+ (x +... + (x)y' + (x)y = 0
то любая их линейная комбинация y(x) = C1y1(x) + C2y2(x) является решением этого однородного уравнения.
2. Если y1(x) и y2(x) — два решения линейного неоднородного уравнения L(y) = f(x), то их разность y(x) = y1(x) − y2 (x) является решением однородного уравнения L(y) = 0.
3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения.
4. Если y1(x) и y2(x) — решения линейных неоднородных уравнений L(y) = f1(x) и L(y) = f2(x) соответственно, то их сумма y(x) = y1(x) + y2(x) является решением неоднородного уравнения L(y) = f1(x) + f2(x).
Обычно именно это последнее утверждение называют принципом суперпозиции.
Дата добавления: 2015-12-17; просмотров: 20; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!